琼州海峡精密高程传递方法研究与试验

胡兴树，欧小善，李 伟，李富强

(国家测绘局第七地形测量队，海南海口570203)

一、引 言

受设备和技术能力限制，一段时期以来，85国家高程基准无法精确传递到海南岛上，海南的高程测量长期以来自成系统，游离于全国高程系统之外，这给海南测绘基准现代化以及琼州海峡跨海通道建设的测绘保障服务带来诸多不利影响，因此，有必要将85国家高程基准精密传递到海南岛上。

跨海高程基准传递的方法通常有静力水准法、动力水准法、GPS水准法及常规大地测量法4种[1]。静力水准法技术要求高，花费昂贵，我国未曾应用过。动力水准法，即验潮法，需要长时间连续的潮位观测资料，周期较长且需要建立验潮站。GPS水准法和常规大地测量法(常用的有精密水准测量和三角高程测量)在我国应用较多，已成功应用于海岛(礁)跨海高程传递和青岛海湾大桥、杭州湾跨海大桥等重、特大跨海工程的长距离跨海高程传递中[1-2]。

本文分别采用GPS水准法和精密测距三角高程测量结合似大地水准面拟合模型计算进行了琼州海峡精密高程传递计算。试验完成后，为海南岛的高程测量纳入85国家高程基准打下坚实的基础，对琼州海峡跨海通道建设具有积极的现实意义，同时也对我国的海岛(礁)中长距离跨海高程传递具有一定的参考作用。

二、跨海高程传递原理

通过GPS和三角高程分别精确测量跨海观测点的大地高高差，结合重力似大地水准面或天文重力水准计算的高程异常结果，综合确定跨海观测点正常高高差。

两点间的正常高差计算公式

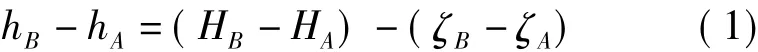
即

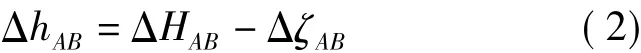
式中，ΔhAB为两点间的正常高高差;ΔHAB为两点间大地高高差;ΔζAB为两点间的高程异常差。

本文通过4种组合计算跨海点点间的正常高高差，经比较分析，推荐精度最优的方法，技术流程图如图1所示。

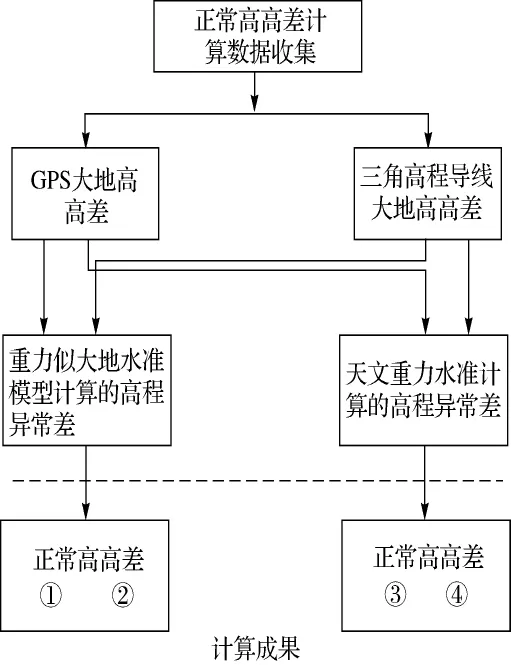
图1 正常高高差确定技术流程图

三、琼州海峡精密高程传递方法及试验

琼州海峡跨海精密高程确定的总体技术流程图见图2所示。

1．琼州海峡跨海大地高高差的确定方法

(1)跨海GPS控制网设计、观测与数据处理

按照有利于观测和长期保存的基本要求，充分考虑GPS卫星接收的地理条件，同时顾及到精密水准联测的方便性，在琼州海峡两岸的海口周围和雷州半岛陆地引测点处，按国家有关技术要求设计，GPS网布测共计35个点位，布设示意图见图3所示。

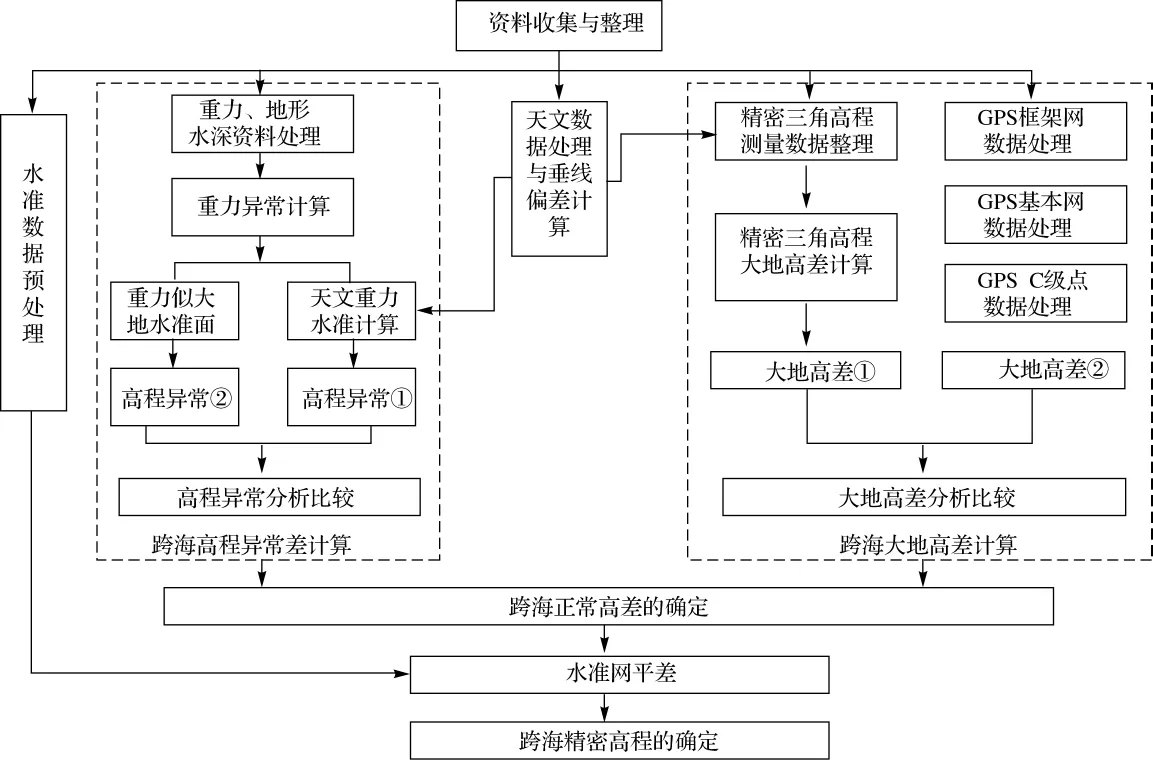
图2 跨海精密高程确定的技术流程图

图3 琼州海峡精密高程传递GPS整网结构

基线处理软件采用GAMIT软件，采用双差相位观测值和IGS精密星历进行基线解算。GPS网平差采用分级平差逐级控制的平差方法，分别在2000国家大地坐标系和WGS-84坐标系(ITRF05，瞬时历元)下约束昆明(KUNM)、泸州(LUZH)、琼中(QION)、武汉(WUHN)、广州(GUAN)、海南大学(HAIK)6个国家GPS连续运行站，做三维约束平差，逐级求解框架点、基本点和跨海高程传递点坐标。

经精度统计表明，基于2000国家大地坐标系与基于WGS-84坐标系的成果精度相当：GPS网点南北方向的精度优于±2．5mm，东西方向的精度优于±2．9mm，高程方向的精度优于±16．0mm。GPS网基线相对中误差最大值为1．82 ×10-7，平均值为8．83 ×10-8。

(2)跨海精密测距三角高程导线测量与数据处理

在琼州海峡较窄的两处白水塘—海口、三塘—南港各选择了一个四边形，进行测距三角高程导线测量(如图4、如图5所示)。外业三角高程观测使用的是高精度瑞士徕卡TCA2003型全站仪，垂直角观测时严格同步，以削弱大气折光的主体部分。

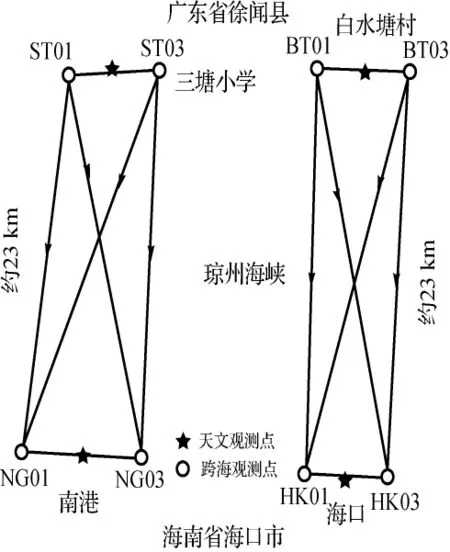
图4 琼州海峡跨海三角高程测量线路

测距三角高程导线测量观测的垂直角是相对于测站垂线方向，利用垂线偏差将垂直角的观测归算至法线方向，再利用参考椭球的严密几何关系得到严密的数学模型，因此，严密的测距三角高程导线计算得到的实际为测站点间大地高高差。

图5 琼州海峡跨海三角高程测量观测墩

经距离化算，并考虑垂线偏差和剩余大气折光，根据精密三角高程导线对向观测大地高差严密计算公式进行对算，获得测站点间大地高高差。

经过精度评价，三角高程测量大地高差中误差的平均值为：三塘小学—南港0．249 1 m，白水塘—海口0．247 6m，均超过中误差限差。根据二等水准测量观测每公里偶然中误差，23 km的水准路线的观测中误差为4．76mm，从高差中误差来看，三角高程导线所计算的大地高差精度远远达不到二等水准测量的要求。

(3)琼州海峡跨海大地高高差的比较与确定

每条测线大地高高差用GPS测量的大地高和用三角高程测量的大地高比较较差结果见表1。

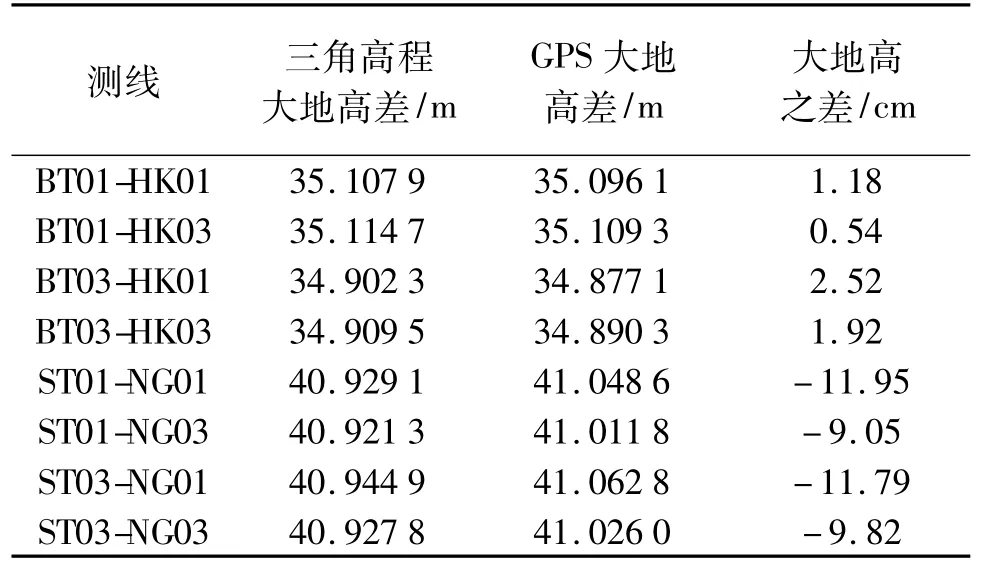
表1 跨海点不同方法测量大地高较差

从表中可以看出，白水塘—海口处的测线大地高吻合较好，差异约为2 cm，三塘小学—南港处的测线大地高吻合较差，差异约为-11 cm。

如前所述，本试验测距三角高程导线方法进行跨海高程传递，不能满足二等水准测量的精度要求，故不采用此方法计算的大地高差传递跨海高程，而采用GPS测量的大地高进行跨海高差计算。

2．琼州海峡跨海高程异常差值的确定方法

(1)跨海似大地水准面精化计算

琼州海峡及周边区域约有实测重力点8600多个，其中广东、广西等陆地区域约有5600点，海南岛约有2100余点，海域地区约有860点。综合利用地形数据、加密重力数据、全球重力场模型完成似大地水准面精化计算工作。

格网空间重力异常的内插计算采用点布格重力异常，利用“移去-恢复”原理计算局部似大地水准。利用跨海北岸的11个GPS水准点(如图6所示)对所有重力大地水准面进行拟合纠正，拟合模型采用二元一次多项式模型，用拟合纠正后的残差中误差作为似大地水准面模型的精度。

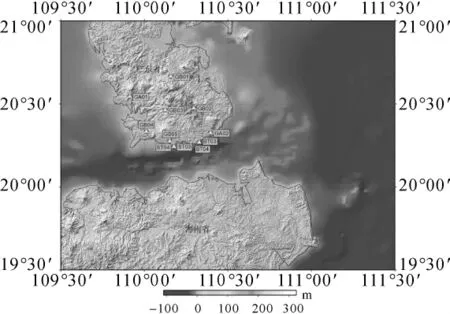
图6 琼州海峡北岸GPS水准点分布

分别采用EGM2008及IGG05B作为地球重力场模型，拟合过程中每种模型计算3个似大地水准面：①GPS水准点拟合前精度最好的;② GPS水准点拟合后精度最好的;③ 拟合前精度最好再经过GPS水准点拟合的。故最后得到6套拟合精度最好的似大地水准面模型。

经分析，以EGM2008作为参考重力场模型进行计算得到的似大地水准面模型中，用GPS水准点拟合后以40 km积分半径所计算的似大地水准面拟合精度最好，拟合精度为7mm。以IGG05B作为参考重力场模型计算得到的似大地水准面模型中，用GPS水准点拟合后以60 km积分半径计算的重力大地水准面拟合后精度最好，拟合精度为8mm。

(2)跨海天文重力水准测量与计算

在选定的跨海高程传递四处观测场地，分别布测了4个天文点，琼州海峡北岸天文观测点为：白水塘村(BT05)、三塘小学(ST05)。琼州海峡南岸天文观测点为：南港(NG05)、海口(HK05)。

天文点纬度采用塔尔科特法观测，经度采用津格尔法观测，经度观测没有测定人仪差。观测使用的仪器型号是DKM3-A，编号为103061。在作业前对天文仪器进行了仪器检验和常数测定、水准器检验和格值测定、天文钟的检验。

利用琼州海峡跨海观测点实测天文大地点成果和高分辨率格网空间异常，采用莫洛金斯基双极函数给出的天文重力水准公式和“移去-恢复”技术直接完成两天文大地点间的高程异常差计算。天文重力水准高程异常段差高程异常计算结果见表2。

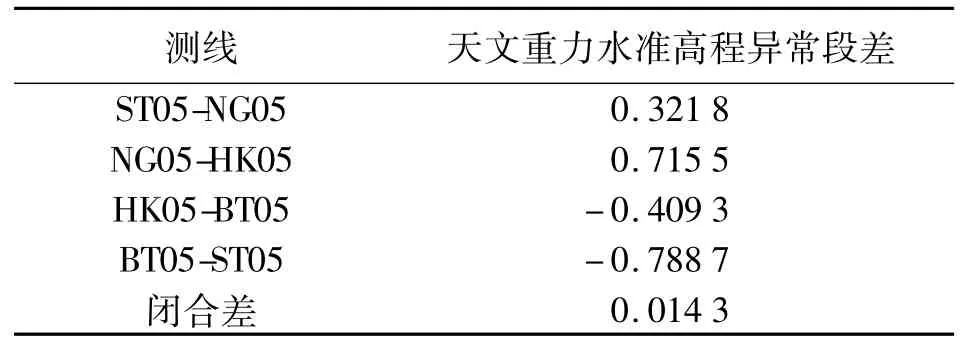
表2 跨海点天文重力水准计算高程异常 m

(3)琼州海峡跨海高程异常差值的比较与确定

利用试验数据计算的似大地水准面及跨海点的2000国家大地坐标系大地纬度、大地经度，采用双线性内插的方法计算跨海点的高程异常，进而计算跨海点之间的高程异常差，与天文重力水准方法计算出高程异常差进行比较分析(比较结果见表3)。结果表面，由IGG05B参考重力场模型所计算的大地水准面模型与天文重力水准附合性在两个跨海处是基本相当的。而由EGM2008参考重力场模型所计算的似大地水准面所计算的高程异常差互差与天文重力水准所计算的高程异常差互差在白水塘—海口方向附和较好，在三塘—南港方向符合较差。

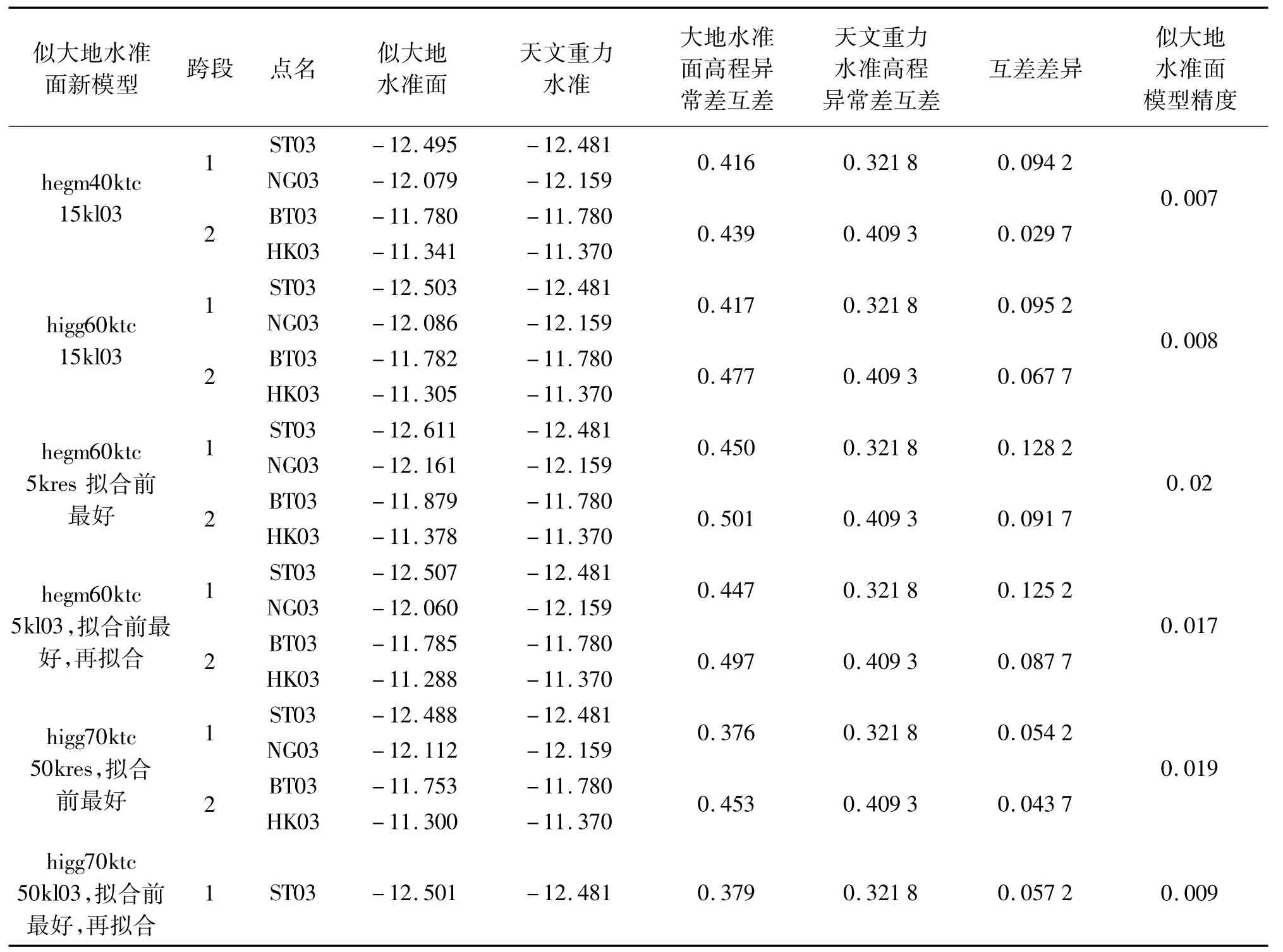
表3 似大地水准面与天文重力水准比较 m

3．琼州海峡跨海正常高的确定与整体平差方法

(1)跨海精密水准联测与数据处理

分别按一、二等水准的要求在琼州海峡两岸布设水准路线并进行选埋和观测。

琼州海峡北岸一侧布测7条支线，琼州海峡南岸一侧布测4条支线，共观测14条路线，总长472．8 km。

环闭合差用经过标尺长度误差改正、正常水准面不平行改正、重力异常改正、日月引力改正后的高差计算，本次水准数据共产生两条附和水准路线。最后，以检测合格后的一等水准点原高程值为起算，对各联测的GPS点及各支线水准点成果进行推算，精度评估结果如下：海安一侧，平差后每公里单位权中误差，m0=2．03mm;海口一侧，平差后每公里单位权中误差m0=2．54mm。

(2)琼州海峡跨海正常高的确定与整体平差

两处跨海点间的正常高高差采用大地高高差结合高程异常差的办法计算。本项目跨海大地高差共有两套成果，分别为GPS大地高差和三角高程导线大地高差，高程异常差有7套成果分别为6种似大地水准面模型计算的高差异常差和天文重力水准计算的高程异常差，相互组合可形成14套正常高差成果。经过精度评价，白水塘—海口方向跨海高程推算精度最高，不同方法计算高差推算海口点与南港点高程差异均小于1．2 cm。

采用跨海两岸精密水准测量计算结果，与跨海点构成一个闭合环，通过平差最终确定跨海点高程。整体平差后跨海高差改正数较小，成果综合比较最优的是：GPS大地高差结合似大地水准面拟合模型hegm40ktc15kl03方法，因此选择该方法计算结果为最终跨海高程传递成果，该方法计算的两处跨海高程传递精度均优于1．2 cm(最终成果见表4)。

表4 琼州海峡精密高程传递最终成果

四、结束语

本文综合运用了卫星定位测量、精密水准测量、精密三角高差导线测量、天文测量、重力归算、天文重力水准、海域大地水准面精化等现代大地测量理论、技术与方法，最终确定通过GPS大地高结合高精度海域大地水准面的方法，实现了琼州海峡跨海高程精密传递，高程传递误差优于1．2 cm。

通过方法研究和试验，对今后中长距离跨海高程精密传递提出以下建议：

1)跨海地区电离层与对流层相对复杂，跨海点的卫星定位观测时间应按照B级网的观测精度进行，才能保证跨海高程传递的精度。

2)长距离跨海高程传递，采用精密三角高程导线方法时，对垂直角观测的精度要求较高，因此跨度越大时，垂直角观测的精度应越高;同时由于临海区域大气折光影响较大，长距离跨海两端大气折光差相差较大，因此建议在进行三角高程导线测量时应同时精确测定大气折光系数。

3)天文观测精度对三角高程导线计算结果影响较大，因此跨海点天文经、纬度的观测均应采用高精度观测方法进行，观测应不低于二等观测精度，同时，应在两岸天文观测点的延长线外20 km左右再增加一个天文观测点，保证每处跨海测线上有4个天文点，可以较精确的计算垂线偏差的影响。

4)长距离三角高程导线测量，采用精密计算方法与采用常规短距离计算方法其计算结果差异较大，因此长距离三角高程导线测量应采用精密计算方法计算。

5)海域大地水准面精化技术已经达到较高的水平，而长距离三角高程导线测量要想确保获得二等水准测量以上的精度，必须精确测定大气折光系数，精确计算垂线偏差的影响并采用精密计算方法，技术要求较高，工作量较大。因此，今后可以采用高精度GPS结合海域大地水准面精化进行中长距离跨海高程的传递。

[1]李建成，姜卫平．长距离跨海高程基准传递方法的研究[J]．武汉大学学报：信息科学版，2001，26(6)：514-517．

[2]李凤斌，柳光魁，王小丽，等．长距离跨海高程基准传递方法及精度[J]．现代测绘，2007，30(2)：7-8．

[3]沙毅，杨德庚．国家三角高程网布测方案研究科研报告[R]．西安：西安测绘研究所，1993．

[4]欧阳桂崇，尹成玉，徐新强，等．基于三角高程测量的跨海高程传递方法[J]．海洋测绘，2011，31(6)：59-62．