基于RCS数据重构调频步进雷达动态目标回波*

晏行伟，陈付彬，张泽建，卢大威，张 军 ，万建伟

(1国防科学技术大学电子科学与工程学院，长沙 4 10073;2 71834部队，河南荥阳 4 50100)

0 引言

调频步进波形具有距离和速度高分辨的潜力，其发射波形为载频步进的chirp信号子脉冲。在总带宽相同条件下，与chirp脉冲相比，降低了系统瞬时带宽;与步进频率波形相比，降低了所需的相参脉冲数。因此调频步进波形兼有这两种信号形式的优点而克服了各自的不足[1]。当采用数字技术时，在不改变硬件结构的前提下，调频步进雷达可变换发射波形和相应的任务算法适应不同的战场态势，最大限度的感知目标信息，然而由于其大带宽和灵活性，增加了信号处理算法的复杂度，当采用Monte-Carlo方法对导引头雷达算法性能进行评估时，迫切需要得到高逼真度的动态雷达目标回波。

传统的目标回波重构方法，一般是从RCS数据中提取目标散射中心模型[4]，再利用雷达信号理论重构回波信号。与之不同，文中直接利用电磁计算软件Radbase计算结果，保留数据高逼真度，将Radbase计算的目标RCS以频率、姿态角为索引保存到数据库。根据线性雷达目标理论，点频RCS序列是目标散射特性函数在频域内的离散采样，将其与入射信号频谱的采样值序列相乘并做逆傅里叶变换，就得到目标的时域回波[5－6]。为了得到满足采样定理的时域回波，要求目标RCS的频率采样较为密集，尤其是在采用chirp发射信号的场合，此时按采样定理需求的目标点频RCS数量对表征目标特性来说是冗余的，若全部用Radbase预测，计算量非常大。文献[9]采用自定制的RCS预测代码，对目标RCS进行频率－姿态角内插，大大降低了计算回波的点频RCS数量。但Radbase计算目标RCS的代码已经固化，无法采用文献[9]的降采样率准则和方法。文中基于线性雷达目标理论和FFT内插方法，根据目标RCS起伏相关频率确定RCS计算频率间隔，而目标姿态角的变化范围全部根据预设的弹、目运动轨迹计算，从而大大降低了调频步进雷达动态目标回波重构的计算量。

1 回波建模和高频区目标散射特性

1.1 调频步进雷达基带回波信号建模

导引头雷达回波信号仿真模拟通常有4种类型，即射频模拟、中频模拟、视频模拟和基带复数据模拟。基带复数据经不同的D/A转换器、滤波器和平衡调制器组合可以分别得到视频信号、中频信号或者射频信号[2]，可见基带复数据模拟是其它3类模拟的基础。基带复数包含了目标全部电磁散射特征信息，获取逼真的回波基带复数据成为回波模拟的关键。

扩展目标雷达回波生成的传统方法是基于散射中心模型的[3]，静止目标的回波基带复信号表达式为:

式中:p(·)=rect(·/T)exp[jπμ(·)2]为chirp脉冲复包络;T为脉冲时宽;μ=Br/T为调频率，Br为脉冲带宽;fc为载频;M为目标散射中心数目;Am为第m个散射中心(s.c.)m的回波幅度;Rm为(s.c.)m到导引头雷达的距离;τm=2Rm/c为散射中心(s.c.)m到导引头雷达的双程时延;c为光速。

1.2 高频区目标散射特性分析

在目标特性研究中，一般采用反射率函数ζ(t)作为目标不同部位的电磁散射特性的时域表征[6]，与目标的冲击响应等价，根据文献[7]，ζ(t)表示为:

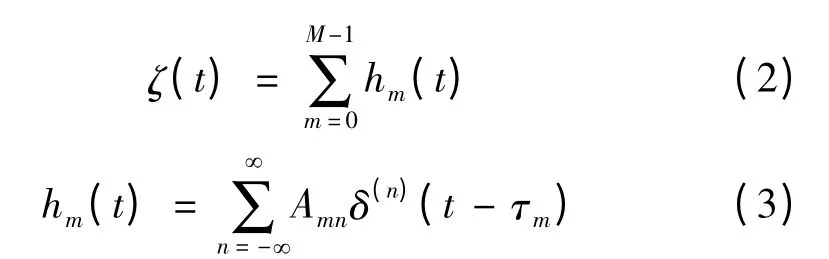
式中，n取正值表示冲击函数δ(·)的n次微分，取负值则表示积分，取0值表示冲击函数本身。

将式(3)变换到频域得到:

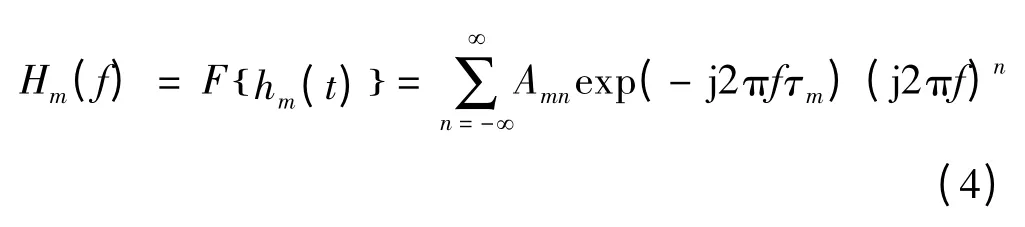
式中:F为傅里叶变换算子，F－1为逆傅里叶变换算子。

导引头雷达通常工作在高频区，故可利用GTD模型[8]，并将n用α代换，式(4)可近似为:

综合式(2)和式(5)，得到目标在高频区的频域特性:

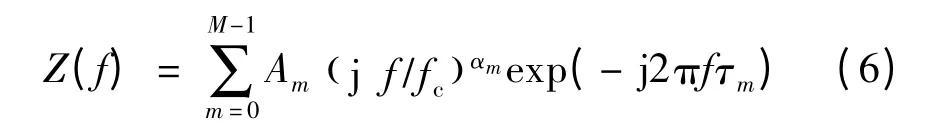
文中研究远场条件下高频区的chirp子脉冲回波信号重构，根据线性雷达目标理论[5]，回波信号频谱是发射信号频谱对目标频谱进行整形后的片段，因此定量刻画发射信号频率范围内的目标频域特性就可以重构回波信号。

2 基于RCS数据重构调频步进雷达回波

文中假设目标满足远场条件，此时RCS与观测距离无关，下面首先分析基于RCS数据重构静止目标的调频步进雷达回波，然后考虑运动目标多普勒效应的影响，得到运动目标回波重构公式，最后获得由较少Radarbase计算得到的复RCS数据生成高动态目标调频步进雷达回波的步骤。

2.1 静止目标回波重构原理

为分解雷达目标回波重构问题，选定目标几何中心作为相位参考点，其也可作为Radbase进行RCS预估的相位参考点。当相位参考点选定后，不同入射角度下的目标反射率函数或复RCS即可唯一确定。

chirp子脉冲发射信号表示为:

式中:Tr为脉冲重复周期，fi为调频步进波形内第i个子脉冲载频。

回波信号se(t，i)表示为:

式中:ζ(t)为目标反射率函数，τ0=2R0/c为雷达与目标几何中心的双程时延，R0为二者之间的距离，卷积符号记作“*”。

将回波信号se与本振信号混频，得到基带回波信号 sb(t)[6]:

根据式(10)，对Sb(f)取逆傅里叶变换得到回波基带信号:

对式(11)进行离散化，设时域复采样率为fs，要求fs大于等于chirp子脉冲带宽Br，则:

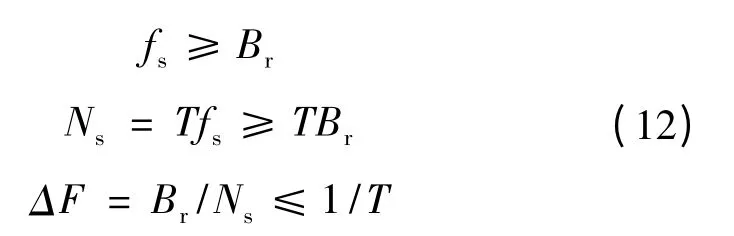
由式(12)可见，chirp子脉冲内采样点数Ns为时宽带宽积，而相邻采样点间频率变化量ΔF为chirp子脉冲未压缩时时宽的倒数。对式(11)进行离散化得到基带回波信号生成表达式(式(13)中，IFFT表示逆快速傅里叶变换):

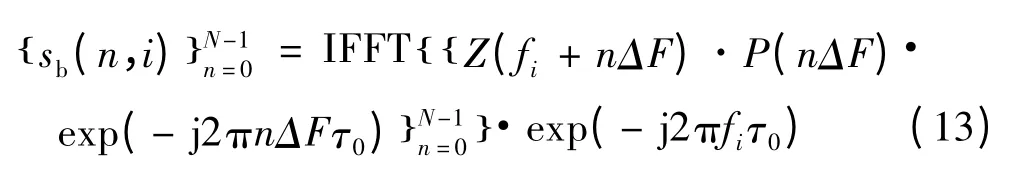
2.2 运动目标回波重构原理

当雷达与目标之间存在运动时，可将多普勒效应等效为发射信号畸变，若两者间径向速度υ以接近为正，则调频步进发射波形中第i个chirp子脉冲的等效表示为:

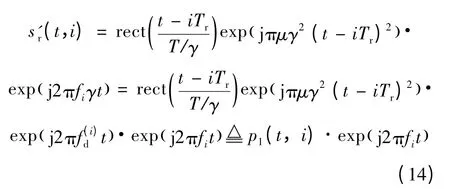
式中γ=1+2υ/c为波形缩放系数。可见，运动情况下，等效子脉冲的时宽、调频率和载频都发生了变化。p1(t，i)为等效子脉冲包络，表示为:

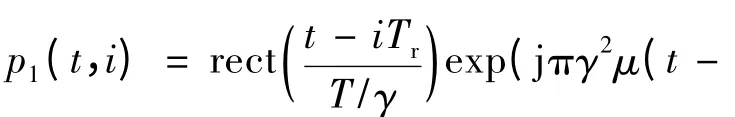
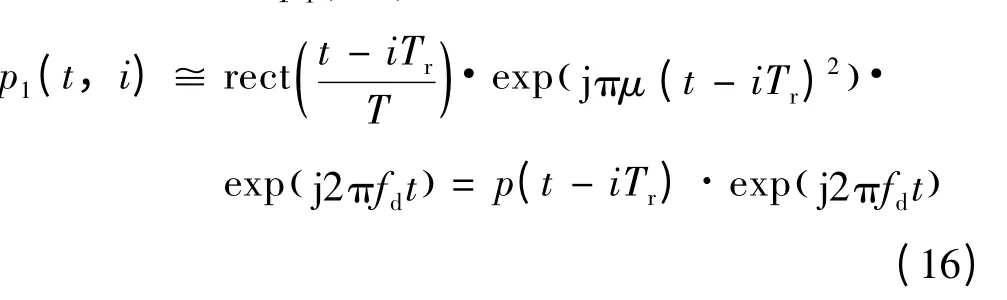
经上述等效变换和近似之后，应用线性雷达目标理论，回波射频信号为:

本振频率fi保持不变，对sr混频，参照式(9)，调频步进雷达的回波基带信号为:

对式(18)进行傅里叶变换，得到:

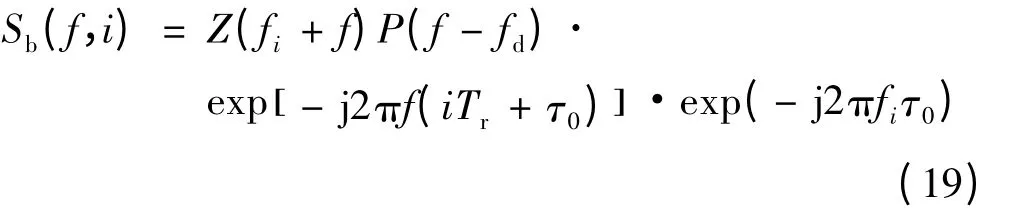
再对式(19)进行离散化，可得:

2.3 仿真计算方法

由式(12)可知，单个chirp子脉冲采样点数N等于子脉冲时宽带宽积，RCS频域间隔等于子脉冲未压缩时时宽倒数ΔF。如果Radbase满足式(12)的原则下计算Z(fn)序列，计算量过大而难以实现。

实际上，Radbase计算Ζ(f)的采样频率ΔFsm应该由目标特性决定。文中采用目标RCS相关频率准则确定ΔFsm。当散射体在目标上均匀分布时，RCS相关频率 fcorr与目标有效尺寸 lr的关系为 fcorr= c/(2lr)[11]，设目标最大可能径向长度为 Lmax，则最小的RCS相关频率为Fcorr≜min{fcorr}=c/(2Lmax)。根据采样定理，当ΔFsm≤Fcorr/2时，就能完全表征目标的频域特征，从而通过内插得到目标在任意频率点的RCS，若取二者相等，则有:

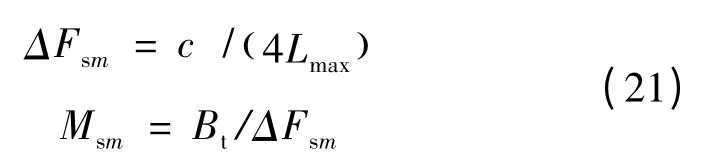
式中:Bt为进行目标回波重构仿真时所关心的总带宽，Msm为通过内插得到带宽Bt范围目标RCS最少所需Radarbase计算的频点数目。

根据频域采样定理[12]，当目标RCS序列可以唯一确定目标散射特征时，利用频域插值公式，可以由该序列内插恢复目标在任意频率处的RCS。仿照文献[13]，当需要内插恢复的RCS序列频率在原始频率序列中均匀分布时，内插过程可由IFFT后接补零FFT进行快速计算;运动目标的多普勒频移可以为任意值，此时可先对原始序列进行IFFT，再乘上一个频移为多普勒频率fd的调制因子[14]，并对调制后的序列进行补零FFT变换，该过程表示如下:

Radbase软件计算的RCS序列为有限长度的，恢复频带内任意点频的RCS只能是近似的，且计算得到的RCS数据在频带边缘会出现纹波，纹波部分必须舍去，这就要求Radbase预估的RCS范围略大于雷达工作频率范围。

综上所述，由满足RCS采样准则的复RCS序列生成高动态目标调频步进雷达回波的步骤如下:

Step 1:确定Radbase进行RCS计算的频率范围，对称覆盖雷达工作频率范围，低端和高端分别超出5%。

Step 2:由式(21)确定RCS计算间隔ΔFsm最大值，并调整ΔFsm，保证调频步进波形步进频率Δf为ΔFsm的整数倍，进而确定总的频点数目Msm。

Step 3:由Radbase计算运动轨迹上姿态角采样序列的多点频复RCS序列，以单个姿态角情况为例，将多点频复RCS序列记作

Step 4:根据式(12)确定chirp子脉冲时域采样率fs最小值，调整fs保证其为Δf的整数倍。

Step 5:存在相对运动时，在chirp子脉冲序列起始计算多普勒频率fd=2υf0/c，由式(19)得chirp等效子脉冲频谱

Step 6:如果相对加速度可以忽略，每个子脉冲时刻的多普勒频率相等，则按照式(22)进行一次运算即可获得整个脉冲串带宽内的RCS插值。否则，必须对每个子脉冲进行单独计算，从中取出对应的RCS序列。

Step 7:利用式(13)或式(20)计算子脉冲回波。

3 算法仿真验证

基于目标RCS重构调频步进雷动态目标回波的数值仿真参数设定如下:雷达目标最大长度设为Lmax=30m，雷达载频f0=10GHz，脉冲重复频率 fr=10kHz，chirp子脉冲带宽Br=15MHz，脉冲宽度T=5μs，子脉冲步进数 N=8，步进量 Δf=10MHz，总带宽Bt=80MHz。为保证输出信号的精度，信号采样率取为40MSps，则每个子脉冲采样点数为Ns=200，脉内采样点的频率间隔为ΔF=50kHz。为重构chirp回波子脉冲，需要获取[f0，f0+80MHz]频率范围内1600个频点的RCS数据。Radbase预估RCS的频率间隔取为 ΔFsm=2.5MHz，范围取为[f0－ 10MHz，f0+90MHz]，这样共需计算40个频率点处的复 RCS数据。

针对某一类型目标，在某一姿态角下，用Radbase计算了[f0－10MHz，f0+90MHz]频率范围内2000个点频的复RCS，抽取其中40个，用以内插恢复长度为2000的复 RCS序列，幅度和相位分别绘图，与Radbase实际计算的RCS对比，示于图1。图中实线为Radbase密集计算的RCS序列，‘+’号为抽取的RCS序列，虚线为内插恢复的序列。为了图示多普勒效应的影响，图1(b)中相对速度取为15000m/s，对应多普勒频率1MHz，从图1(b)中看出，内插的结果序列为原始RCS序列的左移版本，位移量等于多普勒频率，表明采用时域调制与FFT方法可以快速内插任意频率起始的RCS序列。内插RCS序列的首尾两端数据误差较大，舍弃不采用。

为采用仿真实例验证说明回波重构方法的正确性，以文献[4]中的散射中心模型为基础，分别采用两种方法重构目标回波，再经脉压合成目标宽带距离像进行对比。方法1:首先利用散射中心模型生成满足式(12)采样率的目标RCS序列，利用文中方法从该序列重构时域回波。方法2:直接从散射中心模型生成目标回波。由两幅一维距离像可以看出，文中采用的回波生成方法与直接从散射中心产生回波的方法具有很好的逼近效果。

图1 多频点的插值RCS序列与实际计算RCS序列对比

4 结论

文中基于线性雷达目标理论，主要研究了在chirp信号子脉冲照射下动态目标的回波重构问题。提出了一种适用目标电磁特性计算的频域采样原则，即RCS相关频率原则，通过内插方法解决了任意频率点目标RCS估算问题，大大减小了计算量，特别适合于动态场景下调频步进雷达目标回波建模。在验证文中算法时，首先利用散射中心模型生成满足采样准则目标RCS序列，从中重构雷达回波并合成目标距离像，与利用散射中心模型直接生成目标回波并合成的距离像对比，验证了算法有效性。

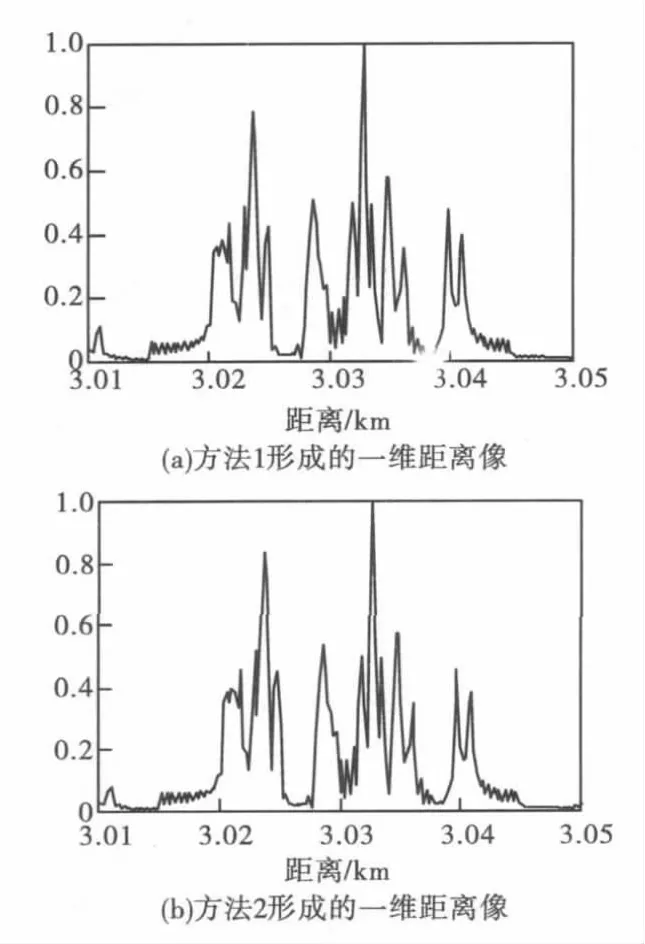
图2 基于内插RCS序列重构回波逼真度验证

需要指出的是，文中所提出的回波重构理论是将目标作为一个整体考虑(仅考虑平动)，故当目标处于远场条件但目标存在绕自身轴向的转动，或者近距离条件下目标各组成部分的多普勒差异不能忽略时，需要从电磁计算数据中提取散射中心模型，对各个散射中心的运动情况进行具体分析，然后采用文中提出的方法生产单个散射中心回波再综合生成整体的目标回波。

[1]贺志毅.合成宽带毫米波雷达导引头的理论及实现[D].北京:航天科工集团第二研究院25所，2002.

[2]张直中.雷达信号的选择与处理[M].北京:国防工业出版社，1979.

[3]保铮，邢孟道，王彤.雷达成像技术[M].北京:电子工业出版社，2005.

[4]E J Hughes.Radar cross section modeling using genetic algorithms[D].Royal Military College of Science，1998.

[5][苏]Л Т Tyчкова.飞行器雷达特性[M].马清海，杨逢春译.洛阳:信息获取与处理技术交流中心出版，1989.

[6]A J Wilkinson，R T Lord，M R Inggs.Stepped-frequency processing by reconstruction of target reflectivity spectrum[C]//Proceedings of the 1998 South African Symposium on Communications and Signal Processing，Rondebosch，1998:101-104.

[7]R A Altes.Sonar for generalized target description and its similarity to animal echolocation systems[J].J.Acoust.Soc.Amer.，1976，59(1):97-105.

[8]L C Potter，Da-Ming Chiang，R Carrière，M J Gerry.A GTD-based parametric model for radar scattering[J].IEEE Antennas and Propagation，1995，43(10):1058-1067.

[9]Yuanxun Wang，Hao Ling.Efficient radar signature prediction using a frequency-aspect interpolation technique based on adaptive feature extraction[J].IEEE Trans.on Antennas and Propagation，2002，50(2):122 －131.

[10]E J Kelly，R P Wishner.Matched-filter theory for highvelocity，accelerating targets[J].IEEE Military Electronics，1965，9(1):56-69.

[11]D K Barton.雷达系统分析与建模[M].南京电子技术研究所，译.北京:电子工业出版社，2007.

[12]史林，赵树杰.数字信号处理[M].北京:科学出版社，2007.

[13]丁丽娟，程杞元.数值计算方法[M].2版.北京:北京理工大学出版社，2008.

[14]A.V.Oppenheim，A.S.Willsky.信号与系统(2nd)[M].刘树棠，译.2版.西安:西安交通大学出版社，1998.