弹载相控阵雷达视线重构研究*

杨雅君，徐胜利，李晓东，廖 瑛

(1国防科技大学航天与材料工程学院，长沙 410073;2上海机电工程研究所，上海 200233)

0 引言

弹载相控阵雷达是相控阵技术在导引头领域的应用，其特点是采用电扫描代替机械扫描，天线波束的切换扫描速度远大于机械方式[1]。而且雷达与导弹弹体固联，只能直接获取相对弹体坐标系的视线角信息[2]。拦截导弹通常采用比例导引规律，必须获得惯性系下导弹－目标视线角速率信息，为获取惯性视线角速率，理论上可以在捷联稳定算法的基础上，通过坐标变换得到惯性视线角，然后采用微分网络获取惯性视线角速率[3]。但该方法会造成噪声放大，并且忽略体视线角和弹体姿态的二阶动态，使得重构性能受导引头采样频率的制约[5]。所以目前国内外的研究大多关注于采用卡尔曼滤波方法来估计目标视线角速率[4－10]，这些文献集中于研究被动导引头“仅测角”(angle/bearing-only measure)条件下的状态估计，而未充分利用主动雷达导引头所能提供的相对距离和距离变化率信息。

针对上述问题，文中引入距离和距离变化率信息，重点研究弹－目相对运动模型和测量模型的建模问题以及系统的可观测性分析，并应用UKF滤波进行状态估计，并根据状态的估计值重构视线角速率。最后给出仿真结果，验证方法的性能。

1 问题分析

弹载相控阵雷达能够测量的信息包括:导弹－目标相对距离R;相对速度R·;弹上视线高低角λz和弹上视线方位角λβ。惯导系统输出弹体系下导弹旋转角速率分量 ωx、ωy、ωz，线加速度分量 ax、ay、az。视线角重构的任务是，根据上述测量信息，重构出高精度的惯性视线高低角qz和惯性视线方位角qβ，及其角速率和。必要的坐标系在表1中列出，坐标系间的几何关系如图1所示。

图1 坐标系间的几何关系

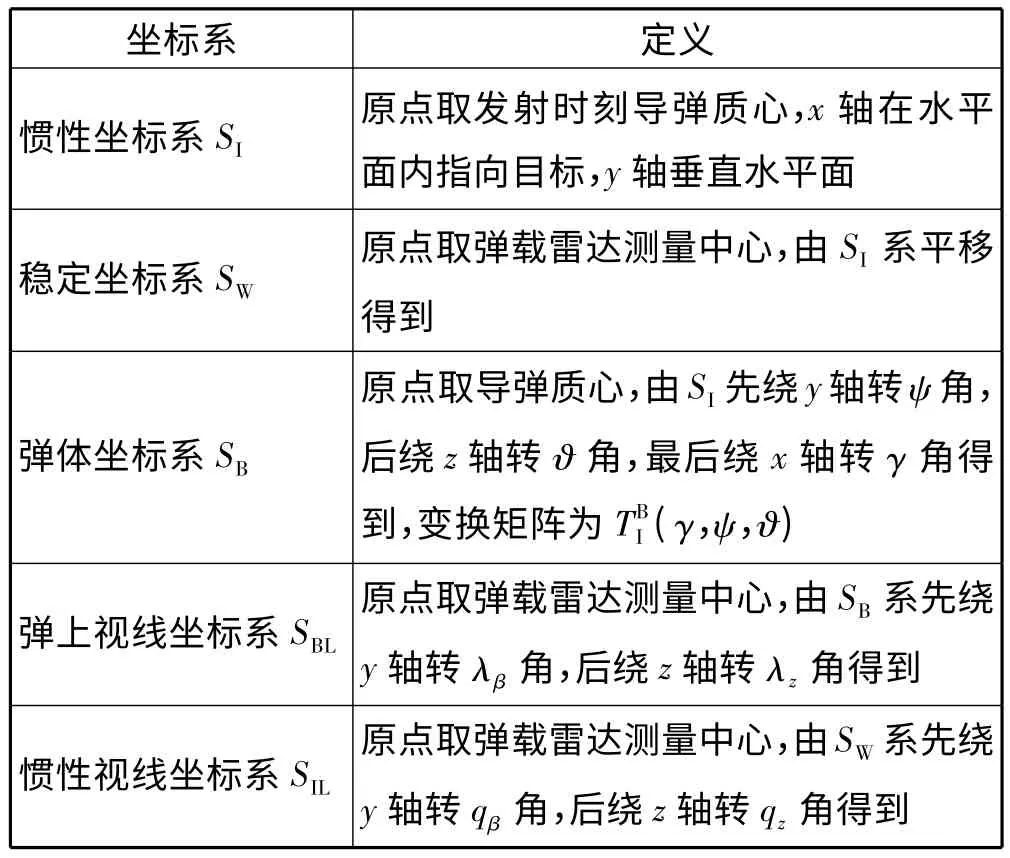
表1 坐标系定义

2 系统建模及分析

2.1 导弹 －目标相对运动模型

设目标与导弹在SI系下运动状态分别为xT和xM，定义导弹－目标相对运动状态为x=xT－xM，并假设机动目标模型为singer模型，则相对运动状态方程为:

式中:

x(k)=[x(k)x˙(k)x¨(k)]T，

ux(k+1)为确定性输入，且:

u(k+1)=Ga˙x(k)=[T3/6 T2/2T]Ta˙x(k)

a˙x(k)为导弹在SI系下加加速度，可根据由弹体角速度和线加速度计算:

wx(k+1)为白噪声序列，其协方差矩阵为:

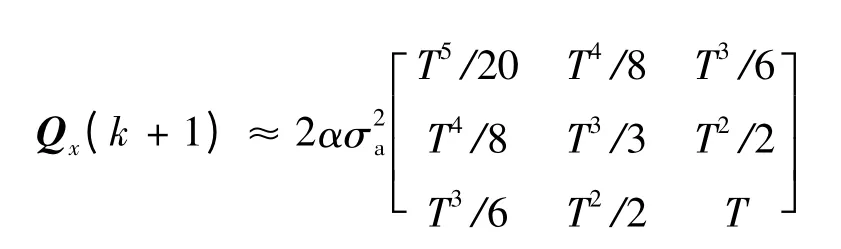
α为机动频率，转弯机动时α=1/60，逃避机动时α =1/20，大气扰动下α =1，当αT足够小时，有:

式(1)描述了导弹和目标在稳定坐标系SW系中的一维运动过程，则其三维状态方程为:

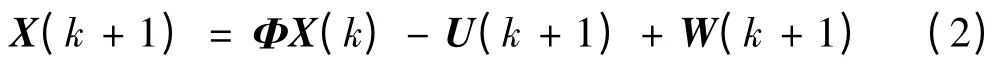
式中:

2.2 测量模型

利用弹上方位角λβ、高低角λz、距离R可以得到目标在SW系下坐标为:

考虑相对速度作为观测量，则观测方程为:

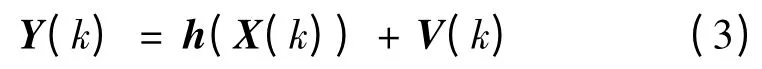
式中:[Y(k)=x(k)y(k)z(k)R·(k)]T;

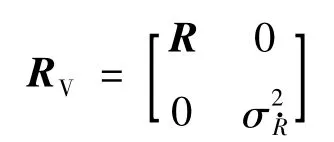
其中:

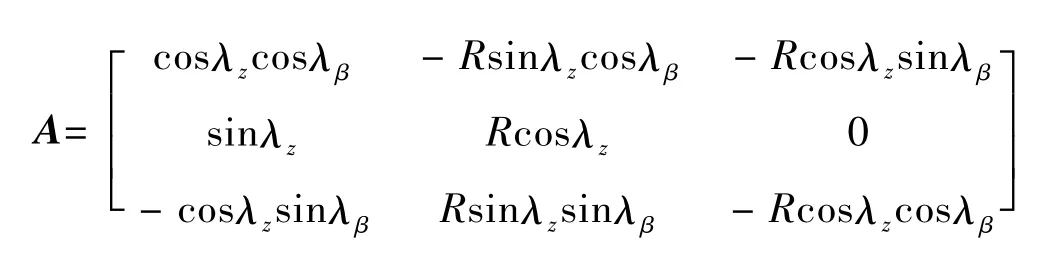
2.3 系统的可观测性分析

系统的可观测性分析包括两方面的内容，一是确定系统状态是否完全可观，二是确定系统的可观测度(DOO)。

不考虑模型误差和测量误差，文中所述系统的连续状态方程和测量方程可分别表示为如下形式:

式中，f(r，v，a)是由导弹制导系统和目标机动模式决定的非线性函数，在离散化的滤波状态方程中假设为高斯噪声。

对于非线性系统的可观性分析，通常利用李导数定义可观性矩阵[9]。由于 f(r，v，a)均值为零，根据李导数定义，式(5)所述系统的各阶李导数为:

由于 ∂L1/∂r、∂L2/∂r、∂L2/∂v的表达式过于复杂，考虑版面有限，文中略写其具体表达式。由李导数定义的可观测阵为:

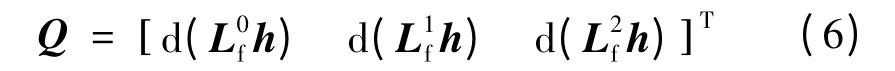
易求得可观测矩阵的秩rank(Q)=9，所以系统完全可观。

对于系统可观测度的分析，一种方法是在Kalman滤波结束后对估计误差协方差矩阵进行分析[10]，得到可观测度定量的分析结果。另一种方法是将可观测矩阵进行奇异值分解(SVD)，并对得到的奇异值进行分析[11]，得到系统可观测度定性的分析结果。鉴于可观测度是系统本身的性质，与滤波过程无关，所以文中采用第二种方法进行研究。

根据矩阵分析理论中的“条件数”定义系统的可观测度[12]:

其中:σmax(Q)和σmin(Q)分别为可观性矩阵的最大和最小奇异值;Cond(Q)为定义的可观性矩阵的条件数，条件数越大，意味着可观性矩阵的行向量或列向量的独立性越弱，系统的可观测程度越低。

由于式(5)所确定的可观性矩阵表达式过于复杂，所以需要采用数值计算进行分析。固定r、v、a中的任意两组状态，计算剩余的一组状态变化时条件数的取值，可分析系统可观测度的变化规律。表2中给出了不同的相对距离、速度、加速度对应下，可观测矩阵条件数的计算结果。

表2 可观测性条件数计算结果

从表2中可以发现，相对速度和加速度对系统的可观测度影响不大，且条件数变化无明显的规律性。相对距离对可观测度影响很大，且条件数随着相对距离的减小而急速增大，说明拦截末期系统的可观测性将严重恶化。

3 基于UKF的视线重构方法

式(2)和式(3)组成的状态 －观测系统中，由于观测方程含有非线性项 R·，鉴于无迹卡尔曼滤波(unscented Kalman filter，UKF)方法对非线性系统状态估计具有较高的精度和广泛的适用性，并且不必求取雅克比(Jacobian)矩阵或海瑟(Hessian)矩阵，具有更简单的计算过程[7]。所以文中采用UKF对相对运动状态进行估计。

3.1 初值选取

根据目标在SW系中的测量坐标[ ]x y zT，并考虑系统状态向量包括了位置、速度和加速度共三阶状态量，所以状态初值需用前三个采样时刻测量值确定:

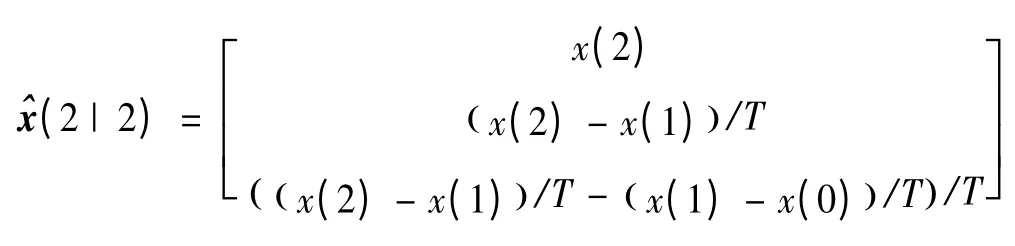
测量坐标[ x y z]T的噪声协方差矩阵如式(4)所示，假设其元素为rij，则初始状态协方差矩阵为:

其中子矩阵Pij为:

3.2 UKF 滤波

UKF滤波过程由以下6个递推步骤完成:

1)计算2n+1个sigma点及其权重;

2)状态值预测;

3)观测值预测;

4)测量更新，更新协方差矩阵Pyy和Pxy以及计算滤波增益矩阵K(k);

5)状态更新;

6)协方差矩阵更新。

UKF滤波是一种常用的非线性系统滤波方法，其具体递推公式在众多文献[5，7，13－15]中有详细的介绍，文中不再赘述。

3.3 视线角速率重构方法

稳定系下导弹－目标相对运动状态量与惯性视线角qβ、qz和视线角速率˙qβ、˙qz间存在下列关系:

综上所述，文中所使用的角速率重构方法可用图2所示的系统框图表示。利用相对运动状态量重构角速率的方法不仅可避免使用微分网络，并且考虑了相对运动的二阶状态量，可以有效减少视线角速率提取的滞后性。

图2 基于状态估计的视线角重构系统

4 仿真验证

4.1 目标机动轨迹和拦截弹道的获取

根据文献[8]建立的导弹飞行力学模型，并取目标机动加速度变化规律为:

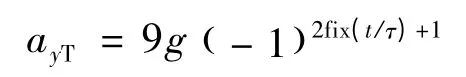
fix(·)为零向取整函数，机动时间常数τ=5s。

利用Matlab/Simulink编制导弹六自由度弹道仿真程序进行数值计算，获得拦截弹道数据。弹道曲线如图3所示。

图3 拦截弹道曲线

拦截过程中，导引规律取有效导航比N=4的修正比例导引律。初始时刻，导弹位置[ 0 11 0 ]km，姿态角 γ =0°、ψ = － 30°、ϑ =30°，速度 Vm0=3.5Ma;目标位置[ 1 0 10 0 ]km，速度VT=300m/s，初始航向 ψcT= － 90°、θT=0°。

由拦截弹道与目标航迹的数据可以计算相控阵雷达和惯导系统测量信息的真值，加上白噪声则为测量数据，噪声的标准差取值分别为:σR=20m，σ·R=1.5m/s，σλ=0.2°，σω=1°/s，σa=0.1g。根据测量数据并采用文中提出的重构方法和滤波算法可以实现对机动目标的惯性视线角速率重构。

4.2 重构结果

假定导引头数据采样周期为12ms，惯导系统与弹上控制系统的控制步长为3ms，设置滤波算法的递推步长与导引头数据采样周期相同。根据式(2)、式(3)及UKF滤波算法，在稳定坐标系SW下对弹－目相对运动状态进行滤波。将状态量的滤波结果代入式(7)、式(8)，以视线仰角通道为例，重构结果如图4和图5所示，分别给出了滤波收敛过程中视线仰角和角速率的重构值与真值的变化曲线。

可以看出，滤波收敛速度很快，收敛后重构值能较精确的逼近真值并反映真值的变化趋势。

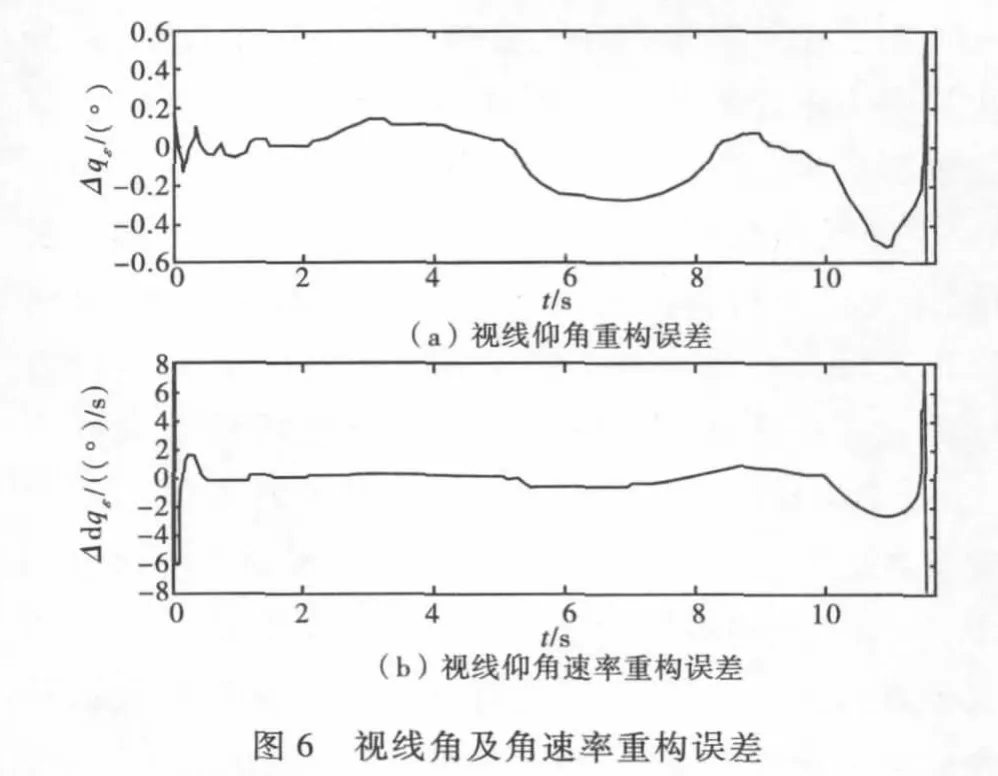
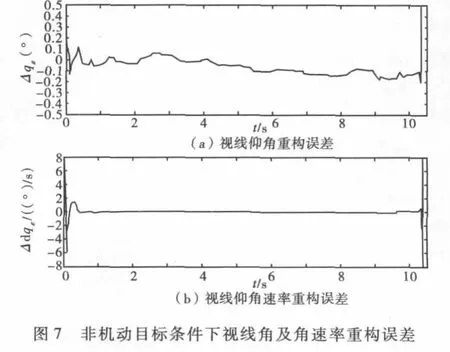
为考察拦截全过程视线重构的性能，将重构值与测量真值相减，得到重构误差。图6给出了拦截全过程视线仰角和角速率重构误差的变化图。可以看到，滤波稳定后视线角重构误差曲线出现有偏波动，且导弹与目标越接近误差波动越大。视线角速率重构误差曲线也表现出类似的情形，并在拦截末段尤为明显。为分析上述情况出现的原因，又进行了对非机动目标的拦截仿真，结果如图7所示。

很明显，在非机动目标条件下，文中所提出的重构方法基本上是无偏重构，但在拦截末段重构误差也出现增大的现象。所以，可以确定，图6中出现的误差偏移源于目标机动，准确的说，是由于滤波模型中目标动力学模型不匹配造成的失调。而拦截末端重构误差增大的现象，也印证了可观测性分析得出的距离越小系统可观测性越差的结论。

4.3 方法对比

采用传统的基于微分网络的视线角重构方法进行计算，其中，对通过微分网络提取的视线角速率信息，通过5阶低通滤波器进行滤波，截断频率为20rad/s，图8以视线仰角速率为例，对真值、微分网络重构值和状态估计重构值进行了对比。

可以看出，文中的方法与传统方法相比，具有更好的视线角速率重构能力。

5 结论

文中在传统视线角速率重构方法的基础上，提出一种基于相对状态估计的重构视线角速率方法，并分析导引头跟踪系统的可观测性。根据弹载相控阵雷达观测数据，实现了对机动目标状态的实时准确估计，并重构出高精度的惯性视线角速率。仿真结果表明:新方法对传统方法的改进是有效的，重构结果精度得到较大提高。该方法不足之处是需要对目标机动模式进行建模，在目标进行机动时，可能造成滤波失调，重构精度下降，另外文中未研究对弹体姿态运动参数的滤波，由于姿态测量噪声加入到视线角重构中，影响了重构精度。如何在目标机动模式改变的情况下进行精确预估，以及设计弹体姿态运动滤波器是今后继续研究的方向。

[1]高烽.相控阵导引头的基本特点和关键技术[J].制导与引信，2005，26(4):1－5.

[2]何庆强，王秉中，殷忠良，等.导引头共形相控阵天线新技术[J].系统工程与电子技术，2006，28(12):1816－1819.

[3]高峰，周辉.一种捷联式数字角信息处理系统[J].制导与引信，2000，21(4):1－11.

[4]周瑞青，吕善伟，刘新华.捷联式天线平台的角跟踪系统设计[J].系统工程与电子技术，2003，25(10):1200－1202.

[5]林喆，姚郁，富小薇.捷联成像寻的器视线重构[J].光电工程，2006，33(3):40－53.

[6]Bertil EKSTRAND.Tracking filters and models for seeker application[J].IEEE Transactions on Aerospace and E-lectronic Systems，2001，37(3):965 －977.

[7]R R Allen，S S BLACKMAN.Angle-only tracking with a MSC filter[C]//Digital Avionics Systems Conference，IEEE，1991.

[8]Won-Sang RA，Ick-Ho WHANG.A robust horizontal LOS rate estimator for 2-Axes gimbaled seeker[C]//Proceedings of the 41st IEEE Conference on Decision and control，IEEE，2002:2884 －2889.

[9]Jacques WALDMANN.Line-of-sight rate estimation and linearizing control of an imaging seeker in a tactical missile guided by proportional navigation[J].IEEE Transactions on Control Systems Technology，2002，10(4):556 －567.

[10]Branko Ristic，M Sanjeev Arulampalam.Tracking a manoeuvring target using angle-only measurements:algorithms and performance[J].Elsevier，Singal Processing，2003，83:1223 －1238.

[11]Titterton D H，Weston J L.Strapdown inertial navigation technology[M].London:The Institution of Electrical Engineers，2004.

[12]Julier S J，Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE，2004，92(12):1958.

[13]钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京:北京理工大学出版社，2006.

[14]黄翔宇，崔平远，崔祜涛.深空自主导航系统的可观性分析[J].宇航学报，2006，27(3):332－337.

[15]Ham F M，Brown T G.Observability，eigenvalues，and Kalman filtering[J].IEEE Transactions on Aerospace and Electronic Systems，1983，19(2):269 －273.

[16]程向红，万德钧，仲巡.捷联惯导系统的可观测性和可观测度研究[J].东南大学学报，1997，27(6):6－10.

[17]高社生，王海维，倪龙强.局部可观测理论在惯性系统快速传递对准中的应用[J].中国惯性技术学报，2007，15(6):642 －645.

[18]孙福明.机动目标跟踪状态估计与数据关联技术的研究[D].合肥:中国科学技术大学，2007.

[19]Vaddi S S，Menon P K.Target state estimation for integrated guidance-control of missiles[C]//AIAA Guidance，Navigation and Control Conference and Exhibit，AIAA，2007.