头部形状和着角对弹丸碰击薄目标前冲过载系数仿真研究*

曹苏雅拉图，王雨时，王 强 ，闻 泉 ，王乃耀

(1南京理工大学机械工程学院，南京 2 10094;2九江45信箱，江西九江 3 32008)

0 引言

引信惯性触发装置设计通常要兼顾钝感度和灵敏度要求。文中对头部不同形状的弹丸以不同着角碰击薄目标过程进行数值仿真，得到弹丸碰击薄目标时的最大前冲过载系数值，从而给引信惯性触发装置设计提供工作环境。

众多文献对头部不同形状的弹丸侵彻过载特性的研究主要侧重于混凝土和钢板等硬目标，Jan Arild Teland等[1]采用LS-DYNA程序研究了截锥形弹丸侵彻混凝土目标的过载特性;聂明飞等[2]利用LS-DYNA软件，对弹丸侵彻多层混凝土靶板进行了数值仿真，讨论了混凝土靶板的破坏现象，研究了卵形头部弹丸对多层混凝土目标的侵彻规律以及目标厚度对弹丸前冲过载特性的影响;徐文峥等[3]采用LS-DYNA软件仿真了尖头形弹丸正侵彻混凝土过程，推导出具有不同几何特点的尖头弹丸侵彻过载数学模型，并得出了锥形和卵形头部弹丸侵彻混凝土靶板的冲击过载特性。孙炜海等[4]对固支薄金属靶板的低速穿透过程进行了评估，给出了锥形头部弹丸穿透金属靶板的耗能公式和弹道极限公式。

1 数值模型

1.1 有限元模型

以某非旋转弹丸质量4.25 kg，碰靶速度为140 m/s为例。另假设弹体外壳厚度1 mm，材料7A04铝合金。根据文献[5]所做的研究，弹体外壳内按土壤处理。为了保证简化后弹丸重量一致，弹长略有不同，但这并不影响仿真结果[5]。弹丸头部几何形状选取为圆柱形、截锥形、半球形和圆锥形，不考虑尾翼结构。靶板为铝合金板、水曲柳胶合板和杉木板(厚3 mm)。整个建模过程采用g·cm·μs单位制。本模型中弹体与靶板之间采用面－面侵蚀接触算法。为节省计算量，建立四分之一模型。不同弹头几何形状的弹丸如图1所示。

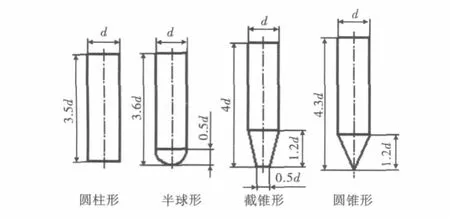
图1 不同头部形状的弹丸

1.2 材料模型及其状态方程

根据文献[6]，采用 JOHNSON-COOK材料模型GRUNEISEN状态方程定义弹体外壳材料的模型和状态方程。JOHNSON-COOK材料模型的本构方程描述了应变、应变速率和温度对流动应力的影响，其表达式为[7]:

式中:σ为流动应变;ε为流动等效塑性应变;ε*m为无量纲塑性应变率;A、B、n、C、m 为材料参数;T*=( T －Tr)/( Tm－Tr)为无量纲温度;Tm为熔点;Tr为室温。

GRUNEISEN状态方程定义了体积与压力之间的关系。其表达式为[7]:

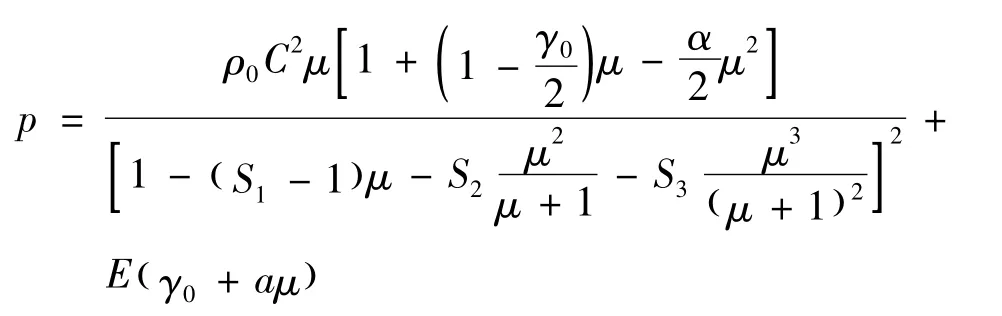
式中:p为材料压力;μ = ρ/ρ0－1;C为 νs－ νp曲线截距;S1、S2、S3为 νs－ νp曲线斜率系数;γ0为GRUNEISEN常数;α为γ0的一阶体积修正;E为材料内能。

用“*MAT_PLASTIC_KINEMATIC”定义弹体填充物。用“*MAT_PLASTI－C_KINEMATIC”定义靶板材料模型。塑性随动模型通过在0和1间调整硬化参数β来选择随动硬化或各项同性，其应变率用COWPER-SYMONDS 模型表示，屈服应力为[8]:

式中:σ0为初始屈服应力;C、P为 C OWPERSYMON DS应变率参数;εepff为有效塑性应变;β为硬化参数;ε˙为应变率;Ep为塑性硬化模量。由参考文献[9－11]，得7A04铝合金、土壤、水曲柳胶合板和杉木板材料模型的仿真参数如表1和表2所列。按照表1和表2设置弹体和靶板材料模型和状态方程参数。

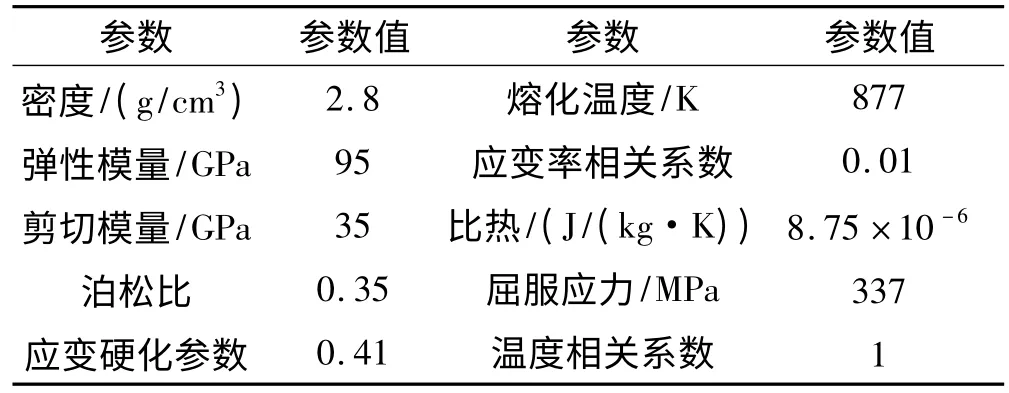
表1 7A04铝合金Johnson-Cook材料模型参数

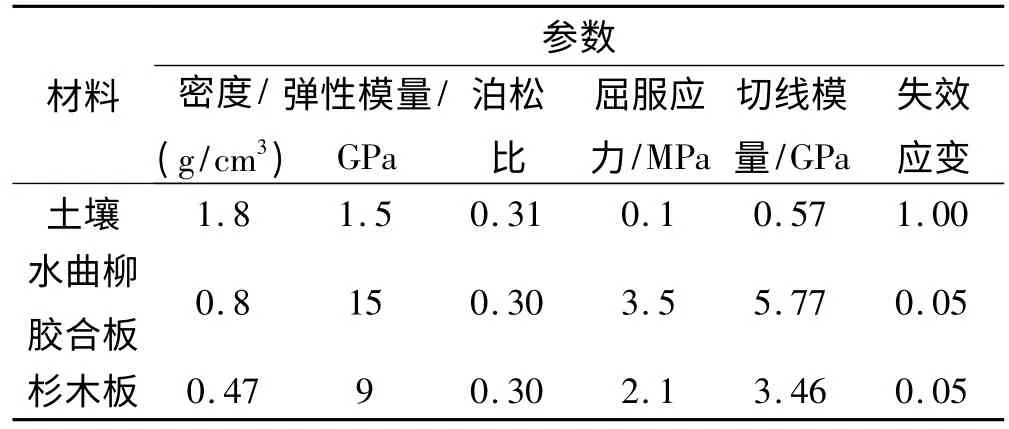
表2 土壤、水曲柳胶合板和杉木板材料模型的主要参数

2 仿真结果

图2 圆柱形弹丸以不同着角碰击三种薄靶板的最大前冲过载系数

2.1 圆柱形弹丸

对圆柱形弹丸以不同着角碰击三种薄目标进行了仿真。以不同着角碰击铝合金板、水曲柳胶合板和杉木板的最大前冲过载系数如图 2所示。碰击铝合金板的最大前冲过载系数值比碰击水曲柳胶合板和杉木板大很多，圆柱形弹丸以小着角和大着角碰击薄靶板的最大前冲过载系数值相差较大，着角变化对最大前冲过载系数值影响很大，碰击三种薄靶板时的最大前冲过载系数值均随着角的增大而单调递减，与着角呈反比关系。弹丸以大于10°着角碰击木质板时着角变化对前冲过载系数影响不大。

圆柱形弹丸以不同着角碰击水曲柳胶合板的前冲过载系数曲线如图3所示。

圆柱形头部弹丸四种不同着角碰击水曲柳胶合板时的最大前冲过载值从大到小依次为:10°、20°、30°、45°、60°和 75°。着角为10°时前冲过载曲线未见波动，随着角的增大前冲过载系数曲线越来越抖动，着角较大时其它三种头部形状的前冲过载系数曲线也有抖动。

图3 圆柱形弹丸以不同着角碰击水曲柳胶合板的前冲过载系数曲线

2.2 半球形头部弹丸

对半球形头部弹丸以不同着角碰击三种薄目标进行仿真。以不同着角碰击铝合金板、水曲柳胶合板和杉木板的最大前冲过载系数如图4所示。半球形头部弹丸以0°～10°着角碰击三种薄靶板时的最大前冲过载系数值变化较小，在此范围内着角对弹丸前冲过载系数影响较小;当以大于10°着角碰击三种薄靶板时弹丸的最大前冲过载系数随着角的增大而减小，与着角呈反比关系。

图4 半球形头部弹丸以不同着角碰击三种不同目标时的最大前冲过载系数

2.3 截锥形头部弹丸

对截锥形头部弹丸以不同着角碰击三种薄目标进行仿真。以不同着角碰击铝合金板、水曲柳胶合板和杉木板的最大前冲过载系数如图5所示。

图5 截锥形头部弹丸以不同着角碰击三种靶板的最大前冲过载系数

弹丸碰击铝合金板时着角变化对最大前冲过载系数的影响较小，最大前冲过载系数值变化范围在250内。碰击水曲柳胶合板和杉木板时弹丸最大前冲过载系数随着角的增大而先增大到最大值后逐渐减小，在着角75°左右时均出现峰值。

2.4 圆锥形头部弹丸

对圆锥形头部弹丸以不同着角碰击三种薄目标进行仿真。以不同着角碰击铝合金板、水曲柳胶合板和杉木板的最大前冲过载系数如图 6所示。头部为圆锥形的弹丸以0°～10°着角碰击水曲柳胶合板和杉木板时最大前冲过载系数值变化较小，此范围内着角变化对最大前冲过载系数影响不大;以大于10°着角碰击时弹丸最大前冲过载系数随着角的增大而增大，到峰值后逐渐变小，未呈现线性变化。弹丸碰击铝合金板时着角变化对最大前冲过载系数影响较小，最大前冲过载的变化范围在200之内，并且着角与弹丸最大前冲过载系数未呈现明显规律，着角小于10°时最大前冲过载系数未呈线性变化，在某一特定角度处达到最大值。

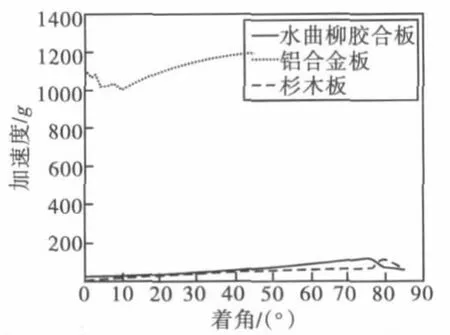
图6 圆锥形头部弹丸以不同着角碰击三种靶板的最大前冲过载系数

2.5 最大前冲过载系数仿真结果汇总

圆柱形、截锥形、半球形和圆锥形四种不同弹头几何形状的弹丸以三种着速和0°～85°着角碰击不同材质薄目标的最大前冲过载系数如表3所列，表中数值单位为g。由表3可看出，四种头部形状的弹丸以大于75°着角碰击铝合金板时均出现跳弹现象。圆柱形头部弹丸以0°、1°、2°和 3°着角碰击水曲柳胶合板时的最大前冲系数值为2190、1784、883和738;截锥形头部弹丸以0°、1°、2°和 3°着角碰击水曲柳胶合板时的最大前冲系数值为357、408、352和226，以上两种情况均是着角对最大前冲过载系数影响大的例证。由圆柱形头部弹丸碰击铝合金板可知，弹丸着角变化对最大前冲过载系数的影响很大，因此布靶引起的着角误差对弹丸前冲过载系数影响很大，且无规律。

四种不同头部形状的弹丸以10°着角碰击铝合金板的前冲过载系数在初始阶段有较大的波动，曲线呈现多个峰值，不像碰击水曲柳胶合板和杉木板一样过载系数曲线呈线性，四种不同头部形状弹丸之间的前冲过载系数峰值相差较大。

此外，按文献[12]提供的弹丸穿透胶合板时的作用力公式计算截锥形弹丸以0°着角碰击水曲柳胶合板的理论前冲过载系数为349.3，仿真结果为356.9，仿真结果与理论估算值相差不到3%，仿真结果与理论估算结果相符合，说明仿真结果是较为可信的。

表3 最大前冲过载系数

3 结论

圆柱形、截锥形、半球形和圆锥形头部形状弹丸小着角(小于10°)碰击3 mm厚水曲柳胶合板的前冲过载系数依次分别为283～2190、103～408、210～229、11～24;碰击3 mm厚杉木板的前冲过载系数依次分别为246～1407、99～249、113～125、10～14;碰击3 mm厚铝板的前冲过载系数依次分别为3917～6810、1854～1913、2707 ～2818、1011 ～1112。圆柱形头部和截锥形头部弹丸的前冲过载系数受着角变化影响较大，因此圆柱形和截锥形头部弹丸应考虑射击试验时布靶误差导致的着角变化以及弹丸攻角变化对引信灵敏度和钝感度试验结论的影响。

四种头部不同形状的弹丸大攻角碰靶时前冲过载系数曲线均呈现较大的抖动，出现多次峰值，故有必要关注这种过载抖动对引信动态特性的影响。

截锥形头部弹丸以不同着角碰击木质靶板时最大前冲过载曲线出现二次峰值，着角和最大前冲过载系数不呈线性关系。广泛应用的截锥形头部弹射击试验时应考虑其前冲过载值不是在正碰时最大，应关注小着角的微小变化对引信钝感度和触发灵敏度试验结果的影响。

半球形头部弹丸以小着角(小于10°)碰击铝合金板的最大前冲过载系数比碰击同厚度水曲柳胶合板大10倍左右，比碰击杉木板大20倍左右。半球形头部弹丸进行射击试验时，选用铝合金靶板相比木质靶板更能有效提高引信触发灵敏度。

圆锥形头部弹的最大前冲过载值比其它三种头部弹丸小很多，说明圆锥形头部弹相比其它三种头部弹丸碰击靶板时所受到的阻力较小。在强度条件得到满足的情况下，设计钝感度要求较高的引信时弹头或弹头引信形状选为圆锥形，可有效提高引信钝感度。

[1]Jan Arild Teland Henrik SjФl.Penetration into concrete by truncated projectiles[J].International Journal of Impact Engineering，2004，30(3):447－464.

[2]聂明飞，李玉龙.卵形头部弹侵彻单多层混凝土靶板有限元仿真[J].探测与控制学报，2009，31(4):78－82.

[3]徐文峥，杨榕.弹药几何因素对过载特性影响的数值分析[J].弹箭与制导学报，2010，30(2):97－100.

[4]孙炜海，文鹤鸣.锥头弹丸低速撞击下薄金属靶板的穿透[J].固体力学学报，2009，30(4):361－366.

[5]曹苏雅拉图，王雨时，王强，等.某尾翼火箭弹碰击薄弱目标前冲过载系数仿真研究[J].探测与控制学报，2012(2).

[6]LSTC，LS-DYNA KEYWORD USER’S MANUAL(VOLUME I)[M].California:Livermore Software Technology Corporation，2007.

[7]陈春黾，李伯龙，聂怍仁.穿甲弹侵彻铝合金靶板数值模拟研究[J].科学技术与工程，2010(14):3442－3445.

[8]尚晓江，苏建宇，王化锋.ANSYS/LS-DYNA动力分析方法与工程实例[M].北京:中国水利水电出版社，2008

[9]王雨时，张德智，曹纯柱.触发引信防雨试验的等效靶板模拟[J].沈阳工业学院学报，1994(3):27－37.

[10]机械工程手册、电机工程手册编辑委员会.机械工程手册(工程材料卷)[M].2版.北京:机械工业出版社，1996.

[11]楼剑锋，王政，洪滔，等.钨合金杆侵彻半无限厚铝合金靶的数值研究[J].高压物理学报，2009，23(1):65－70.

[12]高世桥，王宝兴.截锥形弹低中速贯穿薄靶板时的动力分析与计算[J].应用数学和力学，1986，7(11):1033－1038.