弹道修正弹对单个目标射击的弹药需求量预测模型*

唐 克 ，谢保军，黄 烨

(陆军军官学院，合肥 2 30031)

0 引言

弹道修正弹就是在原有榴弹的引信位置换装成弹道修正模块，由GPS或地面雷达探知飞行中弹丸的实际弹道，再与理想弹道比较，根据偏差大小，指令弹上的修正机构进行距离和方向上的修正。由于这种弹药不需要整体重新研发，而是在原有榴弹的基础上进行改造，使得数以千万计的“笨”弹变得更为灵巧。所以，这种弹药造价低廉，打击效率高，使用方便，对非军事目标的破坏减少，是未来炮射精确制导弹药的发展趋势之一。

普通榴弹射击时，由于火炮自身以及气象条件的影响会产生两方面的误差:一个是诸元误差，另一个是散布误差。而弹道修正弹具有一定的弹道修正能力，因此，即使在火炮射击诸元装定不是很精准的条件下，也能通过自身的修正能力消除诸元误差。即，弹道修正弹射击时只有散布误差。此外，使用普通榴弹射击时，其射弹散布的距离偏差往往比方向偏差大。在目标所在平面上，射弹散布通常是一个纵轴比横轴要长几倍的椭圆。二维的弹道修正弹在方向和距离上都有修正能力，因此其射弹散布近似一个圆，炸点成正态分布，散布中心与目标中心重合，如图2所示。

由于存在以上两个方面的差异，所以传统榴弹的射击效率评定模型以及弹药需求量的计算方法并不能直接用于具有弹道修正能力的新弹种。而简单的根据两种弹种的效能比计算出的弹药需求量既不准确又不科学。为此，文中将提出一种针对弹道修正弹的弹药需求量计算方法。

1 单发弹道修正弹射击效率评定模型

1.1 炸点分布密度的数学模型

要想准确计算出弹道修正弹的射击效率，首先必须弄清楚弹道修正弹炸点的分布规律。经过大量的仿真试验可知，弹道修正弹的射弹散布服从正态分布，这是因为影响弹道修正弹偏差的因素是随机的。假设一发弹落在以目标O为原点的坐标平面上，落点(x，z)的分布密度为 φ(x，z)，如图1所示。再根据(x，z)的正态分布特性可以求得:

图1 目标与落点的位置关系

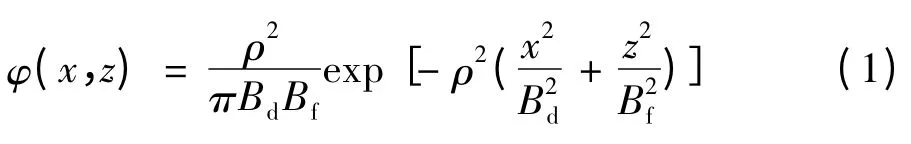
式中:Bd为距离散布中间误差，Bf为方向散布误差，二维的弹道修正弹可以取Bd=Bf;ρ为炮兵常数，表示中间误差与均方差的转换关系，通常取ρ=0.4769。

1.2 单个目标的毁伤幅员

毁伤幅员是一个虚拟的概念，表示炮弹落在该区域内即对目标构成毁伤[1]。

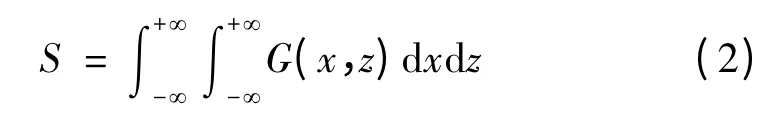
式中:G(x，z)为坐标毁伤率，即一发炮弹落在(x，z)处对目标造成的毁伤程度。

对于单个目标或者密集度较高的集群目标可以采用矩形毁伤率计算其毁伤幅员，也就是将毁伤幅员看作是一个纵深为2lx，宽度为2lz的矩形，这样可以方便计算。

1.3 单发命中概率

单发炮弹命中目标的概率就是随机落点(x，z)落在毁伤幅员S内的概率。图2表示发射500发炮弹后炸点在目标所在平面上的分布效果。

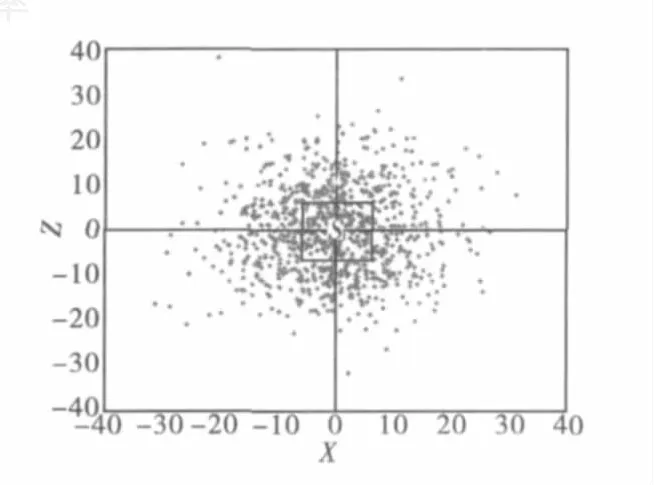
图2 炸点覆盖毁伤幅员的仿真效果

显然，单发命中目标的概率可以这么计算。

设毁伤目标所需要的平均命中弹数为ω，对于不同类型的目标ω的值不一样。ω越大说明该目标越坚固，则毁伤所需的平均命中弹数越多。ω的值可以通过终点爆炸实验或者计算推导得到。再结合式(4)可以得出单发的毁伤概率[2]。

2 弹药需求量计算

在进行弹道修正弹的射击前，首先要分析目标的类型和特点，根据不同的目标计算出确保目标能被摧毁所需的发射数，也就是弹药需求量的先验评估。利用文中介绍的计算方法，可以准确的计算出利用弹道修正弹对单个目标或者密集度较高的集群目标射击时所需的弹药数量。

假设各发命中概率相同，则发射N发至少命中一发的概率为:

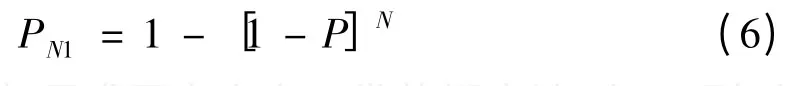
反之，如果求至少命中一发的概率达到Pa，则对式(6)求逆运算可得到最少需要发射的弹数为:

再结合式(5)可知，要求毁伤目标的概率至少达到P'a以上时，所必须的发射弹数为:

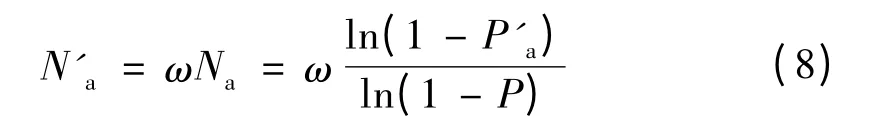
3 模型应用与仿真分析

3.1 模型应用

现使用某型弹道修正弹对某目标进行射击，已知该目标毁伤幅员S=10m×10m，毁伤平均命中弹数ω=2。又知该型弹道修正弹的散布中间误差Bd=Bf=4m，利用上文介绍的方法可以计算出:

1)单发的命中概率

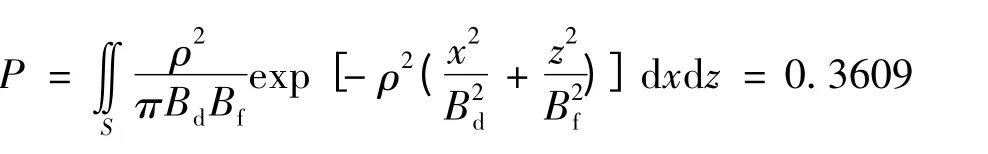
2)若要求毁伤目标的概率不小于0.9，则至少需要发射的弹药量

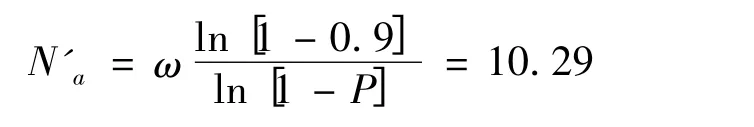
因此，可以说当发射11发弹时，目标被摧毁的概率不小于 0.9。

3.2 仿真分析

根据3.1中所给的参数进行计算机仿真，每次产生11个随机炸点，相当于发射11发炮弹，仿真100次，其统计结果如表1所示。

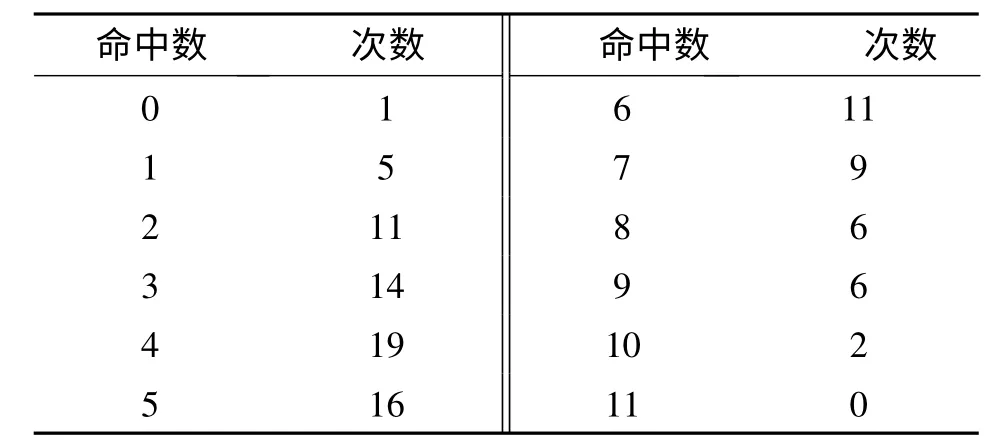
表1 射击仿真统计表

从表1中可以看出发射11发炮弹，命中数小于2发的次数为6，也就是有94次是可以毁伤目标，仿真结果与计算结果相符。

4 结束语

对于多炮射击也可以按单炮的方法计算，这也是弹道修正弹的一个特点。为简化运算模型，文中不考虑空炸的情况，以普通榴弹的射击效率模型为基础，充分考虑了弹道修正弹的弹道以及炸点分布的特点，同时引入毁伤幅员概念，经过分析和层层推导，得出弹道修正弹的弹药需求量计算的数学模型。最后举例分析并利用计算机进行仿真，利用文中介绍的数学模型计算得出的弹药需求量与仿真的结果一致。该方法能够根据目标的特点和所要求达到的毁伤概率快速计算出所需弹药量，计算结果满足要求，可以为炮兵射击弹药需求量预测提供参考。

[1]程云门.评定射击效率原理[M].北京:解放军出版社，1993:128－145.

[2]张飞猛，言克斌，崔万善.炮兵武器系统分析[M].北京:解放军出版社，2008:112－116.

[3]王伟，马志赛.制导炮弹的优势特点及发展趋势[J].飞航导弹，2011(7):18－22.

[4]沙兆军，杨伯忠，刘怡昕.子母弹对集群目标射击的效率评定模型及应用[J].弹道学报，2005，17(4):90－93.