谈二项分布的近似计算及其在保险问题中的应用

张 艳

谈二项分布的近似计算及其在保险问题中的应用

张 艳

泊松定理、棣莫弗－拉普拉斯定理给出了二项分布的近似计算公式，拟对定理中的应用条件进行整理研究，并通过实例，将这两种近似计算公式分别应用于保险问题的计算中。

二项分布;近似计算;泊松分布;正态分布;保险问题

二项分布B(n，p)是概率论中最重要的分布律之一，在研究产品质量、气候状况、工作效能等实际问题中得到了广泛应用。在对这些问题进行决策时，不可避免地要涉及到关于二项分布的计算问题。当n很大时，直接计算是相当繁琐的，若用泊松定理和棣莫弗－拉普拉斯定理得到的近似计算公式计算，则会使计算过程简便的多，但是如果对定理中的近似条件不加以区别，随意使用近似计算公式的话，则会产生较大的误差。为此，首先给出这两个定理，并整理研究定理中n，p的应用条件。

1 二项分布的近似计算

对于服从二项分布的随机变量，我们经常借助以下两个定理进行近似计算:

1.1 泊松定理。

设随机变量X服从二项分布，其分布律为

又设np=λ(λ＞0是一常数)，则有

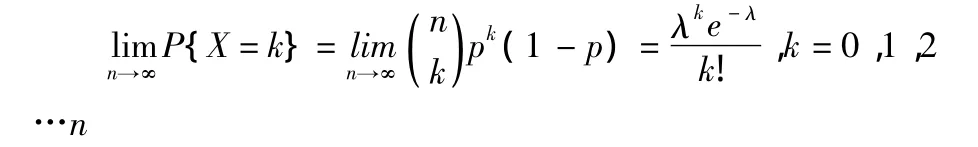
根据定理，可以得到二项分布的近似计算公式:当n充分大，且np=λ(λ是常数)则有

1.2 棣莫弗－拉普拉斯定理。

若随机变量 ηn(n=1，2…)服从参数为 n，p(0＜p＜1)的二项分布，则对于任意x，有

这个定理表明，当n充分大时，二项分布随机变量ηn的标准化变量近似服从标准正态分布，即

我们可以利用上式来计算二项分布概率的近似值，当n充分大时，对于任意正整数x，有

并且由于是用一个连续分布来近似离散分布，在实际应用中，为了减少误差常用如下的修正公式:

对于泊松定理的应用，定理的条件np=λ(常数)意味着当n很大p必定很小，在实际计算中，教材［1］提到，当 n≥10，p≤0.1时就可以用近似公式(1)进行计算，且可以通过查泊松分布表得到结果，计算较为方便。

但是，对于棣莫弗－拉普拉斯定理进行近似计算，公式的应用条件，则简略的多，当充分大时，可做近似计算，这就给初学者或非专业的应用人员造成一种错觉，似乎只要比较大，在任何情况下都可以用公式(3)作近似计算，公式(2)(3)比公式(1)优越得多，但事实并非如此，下面通过一个实例来加以说明。

例1:某种疫苗导致人过敏的概率为0.2%，目前注射该种疫苗的人有1000人，求这1000人中，最终过敏的人数不超过2个人的概率。

设1000人中因疫苗过敏的人数为随机变量X，服从二项分布 B(1000.0.002)，直接计算得

P(X≤2)=P(X=0)+P(x=1)+P(X=2)=0.676677

由公式(1)得

显然公式(1)给出了很好的近似结果，而公式(2)给出的结果则有相当大的误差，用了修正公式(3)以后，虽然减小了误差，但是仍不如泊松分布的近似程度好。虽然由此可见，与公式(1)一样，应用公式(2)，不仅要求n，对p也有一定的要求，换句话说，所谓的n足够大是与p密切相关的。因此在使用公式(2)或(3)时，尤其要注意分析公式的应用条件。在教材［1］中提到，要使np(1－p)＞9，在文献［2］中，作者从数理统计的观点出发，根据显著性水平α，得到了更为精确的结论:当α=0.05时，np(1－p)＞11，当 α=0.01时，np(1－p)＞277。在文献［3］中，作者通过计算机编程，得到了如下结论:当0.1≤p＜0.2，n≥60，当 0.2≤p≤0.9，n≥30。

2 二项分布的近似计算在保险问题中的应用

2.1 保险公司的利润问题。

例2:10000名同年龄且同社会阶层的人参加了某保险公司的一项人寿保险，每个投保人在每年初需交纳200元保费，而在这一年中若投保人死亡，则受益人可从保险公司获得100000元的赔偿费。据生命表知这类人的年死亡率为0.001。试计算:(1)保险公司亏本的概率;(2)至少获利500000元的概率。

解:设X为10000名投保人在一年中死亡的人数，则X服从二项分布B(10000，0.001)

一方面，因为n=10000很大，p=0.001很小，λ=np=10，考虑用公式(1)进行近似计算:

(1)保险公司在这项业务上一年的收入为200×10000=2000000(元)，保险公司在这项业务上“亏本”就相当于{X＞20}，因此所求概率为

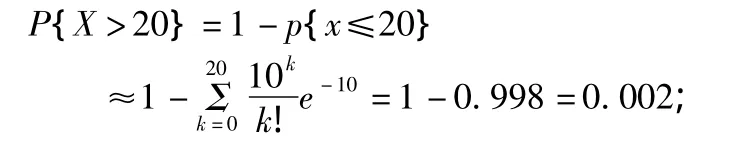
(2)保险公司在这项业务上“至少获利500000元”就相当于{X≤15}，因此所求概率为

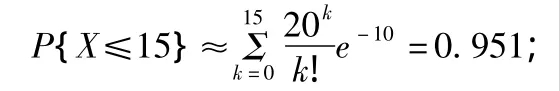
另一方面，因为 n=10000 很大，p=0.001，np(1 －p)=10000×0.001 ×0.999=9.99 ＞9，满足教材中的要求，考虑用公式(3)进行近似计算:

在解决上述例题时，考虑到了公式(3)的应用条件，由此得到的两种近似计算结果相差不到1%，因此可以认为这两种近似方法都得到了比较精确的结果，同时也说明了保险公司亏本的可能性是很微小的。

2.2 保费的确定问题。

例3:有10000名同年龄且同社会阶层的人参加了某保险公司的一项人寿保险，每个投保人在每年初需交纳一定的保费，而在这一年中若投保人死亡，则受益人可从保险公司获得10000元的赔偿费。据生命表知这类人的年死亡率为0.001。若保险公司想以99%的把握保证公司不亏本，试求投保人每人每年需交纳的最低保费额度为多少?

解:设这一年中最大死亡人数为时，保险公司不会亏本，即 P{X≤x}≥0.99

一方面，我们用公式(1)进行近似计算:

另一方面，我们用公式(3)进行近似计算:

查表［1］可得 Φ(2.33)=0.9901，解得 x=17，此时需支出赔偿费17000000，因此最低保费为170元。

由于此时x必须为整数，两种近似结果相差了1，属于正常的误差范围，可以认为这两种近似方法都到了可靠的结果。保险公司为了保证利润，不妨把最低保费定为180元，更有把握盈利。

3 结语

对于二项分布的计算问题，当n很大时，常用泊松定理和棣莫弗－拉普拉斯定理得到的近似计算公式计算。

［1］盛骤，谢式千.概率论与数理统计应用［M］.北京:高等教育出版社，2010.

［2］王雅玲.二项分布近似公式的限制条件及修正［J］.大学数学，2007(6).

［3］杜勋明，陈冬娥，姚云.二项分布和泊松分布的正态近似条件分析［J］.湖北医科大学学报，1998(2).

［4］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京:高等教育出版社:2004(7).

Talk About Approximate Calculation for Binomial Distribution and Application in Insurance

Zhang Yan

Poisson theorem，Di mo eph－Laplace theorem provide us with an approximate calculation formula for the binomial distribution.In this paper，the conditions to adopt the theorem are studied and the two approximate calculation formula are used to calculate the insurance problems.

binomial distribution;approximate calculation;poisson distribution normal distribution;insurance problem

O211.3

A

1672－6758(2012)01－0045－2

张艳，硕士，讲师，江苏科技大学张家港校区基础教学部，江苏·张家港。邮政编码:215600

Class No.:O211.3Document Mark:A

(责任编辑:宋瑞斌)