量子PSO粒子滤波在DR/GPS组合导航系统中的应用*

赵国材，赵 力，宋春雷，刘志德

(1.辽宁工程技术大学电气与控制学院，辽宁葫芦岛125105;2.北京理工大学自动化学院，北京100081)

0 引言

对车辆的全球范围精确定位在军用和民用领域均有很多应用。捷联惯性导航系统(strapdown inertial navigation system，SINS)、航位推算(dead reckoning，DR)导航和全球定位系统(global positioning system，GPS)等都是目前比较常用的定位方式。GPS可以提供绝对的经纬度，是一种易用并且紧凑的导航系统。但由于城市中高楼和隧道对卫星信号的遮挡，GPS并不总是可用，另外还有多通道反射现象的存在［1］，因此，GPS不是最理想的导航方式，通常和惯性导航系统组成组合导航系统，DR导航系统就是其中的一种［2，3］。

DR系统是一种常用的车辆导航系统，它具有实时性好、短时间工作精度高的优点，其关键部分是其惯性单元，但是随着时间的增长，行驶里程的增加，导航系统的误差逐渐积累，并逐步发散。GPS卫星导航系统具有全天候、高精度等特点，且GPS误差不存在累积效应，能够较好地抑制DR导航系统的误差。因此，DR/GPS是比较理想的组合方案。

上个世纪末，Gordon N提出了用大量样本逼近状态分布的粒子滤波(particlefilter，PF)［4］。PF 是一种基于递推贝叶斯估计的滤波方法，但是PF存在着粒子退化、样本贫化和计算量大等缺点，本文将量子粒子群优化(quantum particle swarm optimization，QPOS)算法［5］与 PF 相结合提出了QPSO-PF算法，改善了采样过程，提高了PF的精度，改善了滤波的性能，并将新算法应用于DR/GPS组合导航系统中，跑车实验验证了新算法的有效性。

1 QPSO-PF算法

PSO算法模拟由简单个体组成的群落与环境以及个体之间的互动行为，通过群体中个体之间的协作和信息共享来寻找最优解［6］。量子计算是利用量子系统的叠加性、并行性和量子纠缠等特性实现比经典计算更为高效的计算模式［7，8］。

本文提出的QPSO-PF算法使用量子位对粒子进行编码，同时引入量子旋转门与量子变异操作保持粒子集的多样性，使粒子集有效逼近后验概率密度函数，加速了粒子集的收敛，进而提高了PF的精度，从而取得了良好的滤波性能。

综上所述，QPSO-PF算法流程如下:

式中 xk∈Rn为状态向量，wk－1为系统噪声，vk为量测噪声。

式中 θij=2π× rand，i=1，2，…，m;j=1，2，…，n，rand 为(0，1)之间的随机数，m是种群数。

4)计算每个粒子的适应度，计算得到粒子的个体极值位置和全局极值位置。

5)按照式(3)，式(4)实现粒子状态更新，按照(5)实现粒子的变异。位置更新方程

政府必须回归到市场经济下政府的职能本位上来，将“经济建设”的职能交还给市场，政府要履行好公共财政的基本职能。首先要正确地认识什么是真正的公共财政，就是怎么样去定位政府与市场的关系，政府究竟应该做什么？过去我们经常讲，政府包办天下，政府做了太多管不好也管不了的事，今天“万能政府”的影子还见诸各个行业，凡是国家权力干预的地方和行业必然是效率低下和垄断程度很深的。我们的微观经济生活管得太深、管得太死，要回归到政府的公共财政的建设上面，把资源配置和经济建设的职能主体要交还给市场和私人部门。

式中 i=1，2，…，m;j=1，2，…，n。

速度更新方程

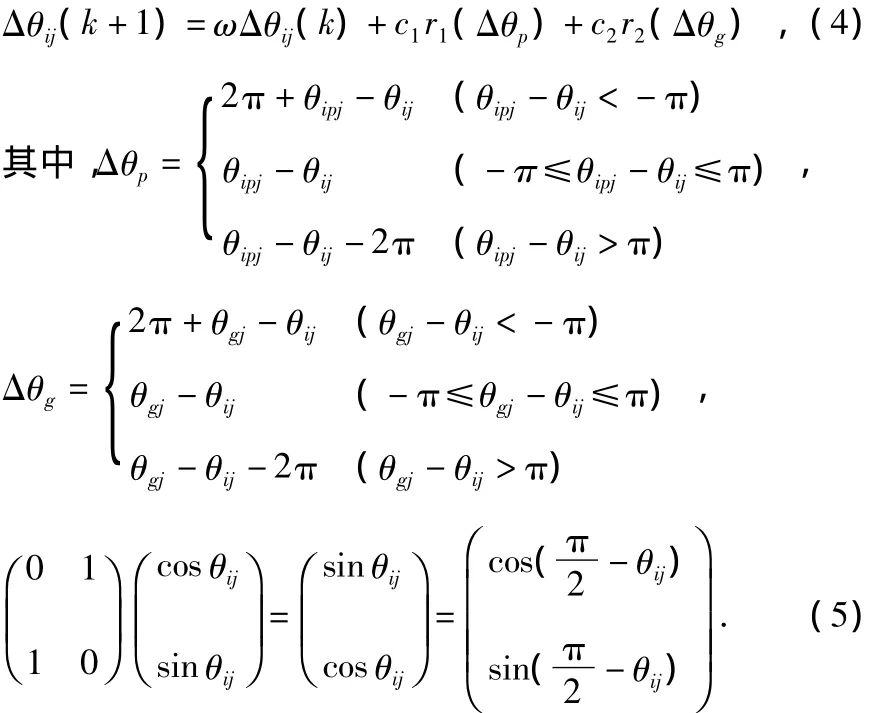
6)若满足收敛条件或达到最大迭代次数，跳到步骤(7)，否则，返回步骤(4)。

7)按照式(6)计算对应粒子的重要性权值，归一化权值

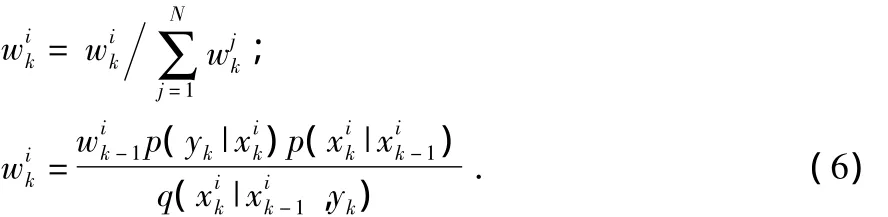
8)利用式(7)对xk进行估计;k=k+1，返回步骤(2)

2 陆用组合导航系统模型与实验

2.1 导航系统组成与模型

陆用组合导航系统主要由方位保持仪、寻北仪、控制显示器、航向指示器、高程计、里程计和GPS等部分组成，如图1所示。

图1 陆用组合导航系统组成Fig 1 Composition of land combined navigation system

陆用组合导航系统以DR导航系统为主要导航系统，以GPS作为辅助，实现组合导航。DR方法是根据航向和里程信息，推算得到车辆的位置信息，里程信息由里程计提供，航向信息由方位保持仪提供。设车辆的起始位置为(x0，y0)，Sn和θn是从n－1时刻到n时刻车辆行驶的路程和航向，则车辆n时刻的位置为

航向误差体现在实时航向数据上，里程误差体现在里程系数误差上。设航向误差为ζ，里程系数为k，里程系数误差为ξ，车轮转一周里程计输出脉冲数为N，第i段距离内里程计脉冲数为ni，采样间隔为500 ms，由式(8)可得

以DR系统与GPS在北向和东向的定位偏差vxn和vyn作为观测量，则有量测方程为

2.2 里程系数与航向误差辨识

设观测向量为υn=［υxn，υyn］T，使用 QPSO-PF 方法，根据里程系数误差和航向误差的先验概率分布产生两组粒子，依照观测向量υn对粒子分布进行调整。设观测向量υn的范数为‖υn‖，如果粒子使范数‖υn‖计算数值较小，则认为该粒子出现机率较大;反之，则认为此粒子出现机率较小。依照粒子出现的机率对粒子分布重新调整。通过调整后的粒子对ζ和ξ进行估计。用估计结果对里程系数和航向进行修正，能够抑制DR导航系统误差的增长，提高导航定位精度。

里程系数误差ξ主要与轮胎和地面状况以及车辆负荷等因素相关。设用一组粒子{ξ1，0，ξ1，0，…，ξNp，0}描述里程系数误差的初始概率分布p0(ξ)，Np为粒子数目，粒子初始分布为均匀分布。航向误差主要来自于初始寻北误差和陀螺仪随时间慢慢积累的漂移。用一组粒子{ζ1，0，ζ2，0，…，ζNp，0}描述航向误差的初始概率分布p0(ζ)，粒子初始分布为均匀分布。由式(9)，根据n时刻观测向量vn对粒子分布进行调整。

里程系数误差和航向误差辨识的QPSO-PF具体步骤如下:

1)初始化随机样本:根据里程系数误差和航向误差的先验概率分布 p0(ξ)和 p0(ζ)，抽取初始随机样本{ξ1，0，ξ1，0，…，ξNp，0}和{ζ1，0，ζ2，0，…，ζNp，0}。

2)采用QPSO-PF算法进行粒子更新:依照n时刻的观测向量 vn对粒子分布进行调整。考虑随机样本 ξ1，n－1，ξ2，n－1，…，ξNp，n－1和 ζ1，n－1，ζ2，n－1，…，ζNp，n－1，根据范数‖vn‖将样本中出现机率较大的粒子进行复制;将出现机率较小的进行舍弃，得到新的随机样本 ξ1，n，ξ2，n，…，ξNp，n和 ζ1，n，ζ2，n，…，ζNp，n。

3)对参数进行估计:由 n 时刻粒子样本 ξ1，n，ξ2，n，…，ξNp，n和 ζ1，n，ζ2，n，…，ζNp，n，可以计算

4)取n+1→n ，返回步骤(2)，并重复下去。

2.3 跑车实验

跑车实验从北京西三环某地出发，行驶里程约为24 km，所用时间约为30 min，跑车路线如图2所示。图3为跑车实验中的DR/GPS组合导航，跑车过程中记录DR和GPS数据，并进行离线滤波处理。

图2 跑车路线图Fig 2 The route of test

图3 DR/GPS组合导航系统Fig 3 DR/GPS integrated navigation system

采用PF算法和QPSO-PF算法对记录的跑车数据进行滤波。设粒子数目为500。估计里程系数误差ξ时，在区间［k(1－15%)，k(1+15%)］内均匀产生粒子;估计航向误差ζ时，在区间［－60，+60 mil］范围内均匀产生粒子。PF算法和QPSO-PF算法对里程系数误差滤波的结果如图4所示;对航向误差滤波的结果如图5所示。

因为GPS信号是在400 s左右开始有效的，所以，对里程系数误差和航向误差的滤波是从400 s开始的。从图4和图5可以看出:采用QPSO-PF算法对里程系数误差和航向误差进行滤波，里程系数误差估值^ξ约从－0.058×10－3m/Nr变化到0.019×10－3m/Nr;航向误差估值^ζ约为－6.2～－1.7 mil。由于存在未标定的安装误差和初始寻北误差及动态方位漂移误差，航向误差对DR导航系统误差影响较大，使DR导航系统精度明显下降，而里程系数误差对DR导航系统误差影响较小。

在跑车实验中，车辆最终停留在一个标准点上，通过和标准点的数值比较，可以确定导航系统的定位精度。将PF算法和QPSO-PF算法估计出的里程系数误差和航向误差反馈到DR导航系统中，对里程系数和航向进行修正，修正的DR误差如表1所示。采用PF算法对里程系数误差和航向误差修正后，DR误差较大，定位精度约为0.171%;采用QPSO-PF算法修正后，DR导航系统获得了较高的定位精度，约为0.125%。这表明，QPSO-PF算法能够有效地抑制了DR导航系统误差的增长，提高了组合导航系统的定位精度。

图4 里程系数误差估计对比曲线Fig 4 Contrastive curves of error estimation of mileage coefficient

图5 航向误差估计对比曲线Fig 5 Contrastive curves of error estimation of azimuth

表1 DR导航系统误差对比Tab 1 Error contrast of DR navigation system

3 结论

本文将QPSO算法与PF算法相结合，提出一种QPSOPF算法。该算法充分利用了量子优化的叠加性、并行性和加速功能等特点，在QPSO的搜索寻优过程中，使用量子优化控制粒子的运动方向，防止粒子过分密集，保证了粒子集的多样性。新算法有效地改善了粒子的分布，加速了粒子集的收敛，获得了更快的收敛速度和全局寻优的能力，进而提高了PF的精度，取得了良好的滤波性能。将QPSO-PF算法应用到陆用DR/GPS组合导航系统中，根据GPS定位信息对DR导航系统中的航向误差和里程系数误差进行估计，并对里程系数和航向进行修正，跑车实验验证了该算法的有效性。

［1］Kaplan E D，Understanding GPS:Principles and applications［M］.Artech House，1996.

［2］Zhao L，Ochieng WY，Quddus M A，et al.An extended Kalman filter algorithm for integrating GPSand low cost dead reckoning system data for vehicle performance and emissions monitoring［J］.Journal of Navigation，2003，56(2):257－275.

［3］Zhao Y.Vehicle location and navigation systems［M］.Artech House，1997.

［4］Gordon N，Salmond D.Novel approach to nonlinear/non Gaussian Bayesian state estimation［J］.IEE Proc of Radar and Signal Processing，1993，140(2):107－113.

［5］Moore P，Venayagamoorthy G K.Evolving combinational logic circuits using a hybrid quantum evolution and particle swarm inspired algorithm［C］∥Proceedings of the 2005 NASA/DoD Conference on Evolvable Hardware，2005:97－102.

［6］纪 震，廖惠连，吴青华.粒子群算法及应用［M］.北京:科学出版社，2009.

［7］夏培肃.量子计算［J］.计算机研究与发展，2001，38(10):1153－1171.

［8］金乃高，殷福亮.量子进化粒子滤波算法及其在说话人跟踪中的应用［J］.信号处理，2008，24(6):982－987.

［9］李士勇，李盼池.量子计算与量子优化算法［M］.哈尔滨:哈尔滨工业大学出版社，2009.