挠性陀螺解耦控制在工程中的实现

王 平，杨 静，高英俊，姚军军

(1.西安理工大学机械与精密仪器工程学院，陕西西安710048;2.中航工业陕西华燕航空仪表有限公司，陕西汉中723102;3.驻012基地军事代表室，陕西汉中723100)

0 引言

挠性陀螺仪作为一种双轴输入—双轴输出的惯性速率敏感器，具有精度高、体积小、功耗低等优点，因而得到广泛的应用［1］。然而，在战术导弹的稳定光电瞄准系统和飞机捷联惯性导航等系统中，对陀螺动态性能提出更高要求。在某机载稳瞄搜索系统中，挠性陀螺作为测速反馈元件，其敏感方向作为反复摆动搜索的目标，由于挠性陀螺仪在方位与俯仰方向的耦合，当方位(俯仰)方向的搜索镜头由正转变逆转或由逆转变正转时，挠性陀螺仪俯仰(方位)方向上将产生明显的抖动，造成搜索和定位产生误差，导致稳瞄搜索系统的性能降低。因此，解决挠性陀螺动态过程中的耦合量已经成为一个急需解决的问题。

目前，国内已有高校和研究院所对挠性陀螺的解耦问题进行了研究［2，3］，然而理论方法设计的再平衡回路解耦控制网络，由于算法过于复杂，在工程实践中采用模拟电路很难实现，因此，到目前为止，国内挠性陀螺仪实际生产中，并没有考虑解耦问题，只是将系统简单处理为单输入单输出的系统。本文在深入研究挠性陀螺理论的基础上，结合挠性陀螺仪具体参数和工程实际应用情况，提出了一种适用于工程应用的简化解耦控制算法，并通过仿真、试验证明了本方法的有效性。

1 挠性陀螺传递函数

挠性陀螺是一种双输入—双输出的速率敏感器，在力反馈状态下可以测量沿2个输入轴的角速率信号。由于结构方面的原因，它的2个输入—输出之间存在着严重的耦合，这种耦合是双重的，即一个轴上的输入角速度能够同时在2个输出轴上产生反馈力矩。

挠性陀螺仪传递函数模型为

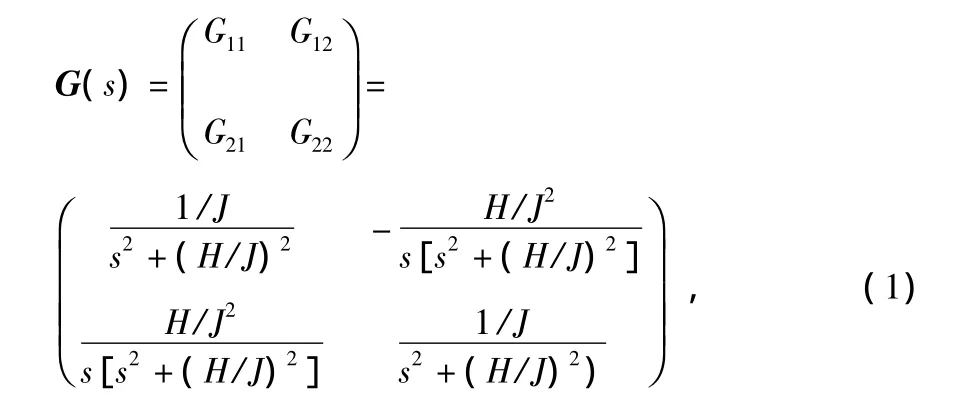
式中 J为陀螺转子的赤道转动惯量。由上式中可见，G12(s)和G21(s)为陀螺仪的主传输项，表示陀螺仪的进动特性;G11(s)和G22(s)为陀螺仪的交叉耦合项，是不希望存在的耦合项［4］。

2 模拟再平衡回路与解耦控制网络设计

2.1 模拟再平衡回路模型

模拟再平衡回路以其线路简单可靠、体积小、成本低、较易实现大范围角速度跟踪等优点被广为应用［5］。目前，国内挠性陀螺组件多以模拟再平衡回路为主，挠性陀螺仪的再平衡回路模型如图1，其中，ω=［ωx，ωy］为陀螺仪外界角速率输入，θ=［θx，θy］为陀螺转子相对壳体产生的夹角输出;I=［Ix，Iy］为再平衡回路控制电流。Kp为信号器刻度系数，K为采样电阻的倒数，将控制电流信号转换成电压信号输出，Kt为力矩器刻度系数，K(s)为校正电路传递函数，M=［Mx，My］为流过力矩器的电流产生的作用在陀螺转子上的力矩。

实际工程中，挠性陀螺输出检测一般为控制电流I。由于式(1)中挠性陀螺存在耦合，解耦控制网络D(s)=［D11，D12，D21，D22］的作用就是使得待测的2输入轴角速率ω与2输出轴输出电流I成一一对应关系。

由图1，可以得到

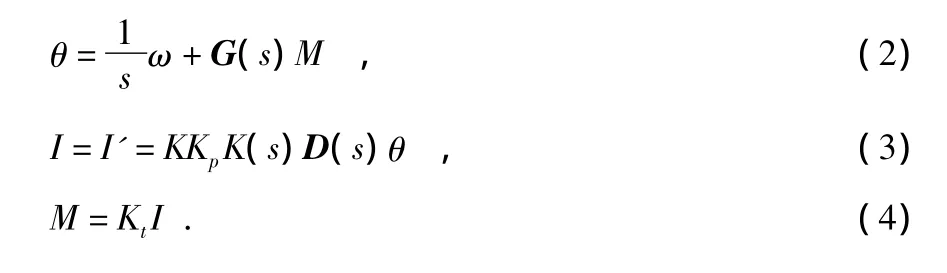
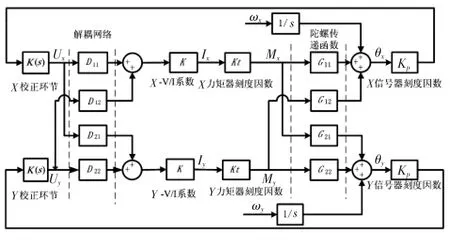
图1 模拟再平衡回路控制模型Fig 1 Control model of analog of rebalancing loop

并将式(5)代入式(3)得到

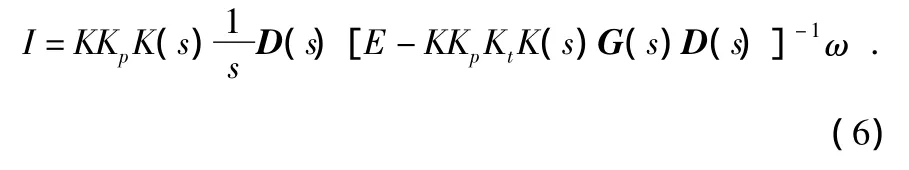
2.2 工程解耦控制网络的设计

令P(s)=KKpKtK(s)，于是

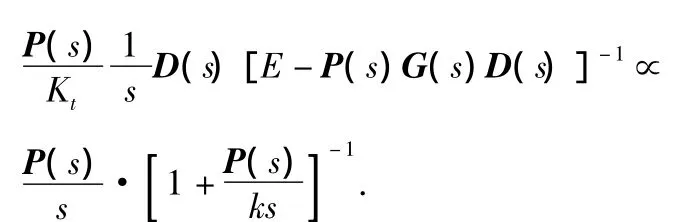
为将式(6)对角化，取

式中 k为一个待定系数，E1=［0，-1;1，0］。

对式(7)左端求逆有

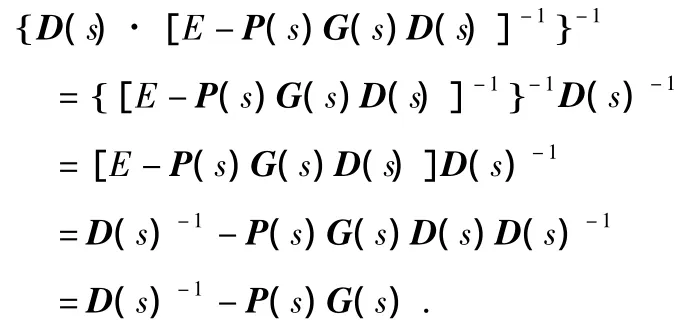
对式(7)右端求逆有

于是，得到解耦阵

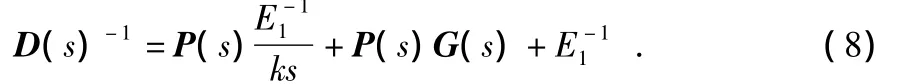
理论上，陀螺仪再平衡控制回路中加入由式(8)得到的解耦阵D(s)后，即由1个相互影响的双轴系统变成2个完全独立的系统。但式(8)中带入式(1)的挠性陀螺G(s)模型得出的解耦网络D(s)比较复杂，在电路上几乎无法实现。为此，需要对解耦控制网络的计算进行工程简化。

3 工程简化解耦算法仿真与试验

通常，陀螺传递函数均指陀螺信号器夹角对作用于转子力矩这种情况，理想情况下，根据工程上挠性陀螺的实际参数，为了计算出近似的解耦控制网络，可以忽略陀螺仪传递函数矩阵的二阶项，挠性陀螺一阶传递函数为

式中 θy(s)为陀螺转子绕Y轴的转角，rad;Mx(s)为作用在陀螺转子X轴上的力矩，N·m;H为陀螺转子(含内外环等)的角动量，kg·m2。简化陀螺传递函数矩阵数学模型为

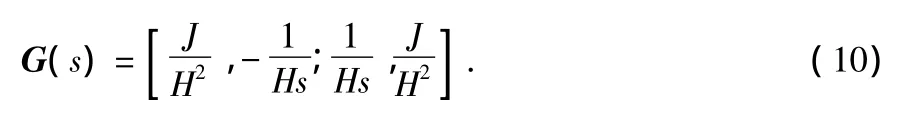
以国营一四一厂的某型挠性陀螺仪为例，陀螺仪转动惯量J=0.009 kg·m2·rad/s，陀螺转子(含内外环等)的角动量，H=14.92 kg·m2;带入式(10)可得简化系统模型

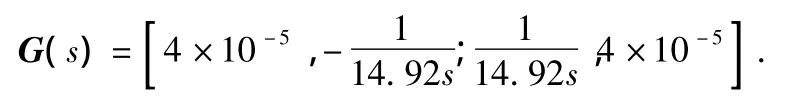
根据式(8)可计算出解耦控制网络D(s)

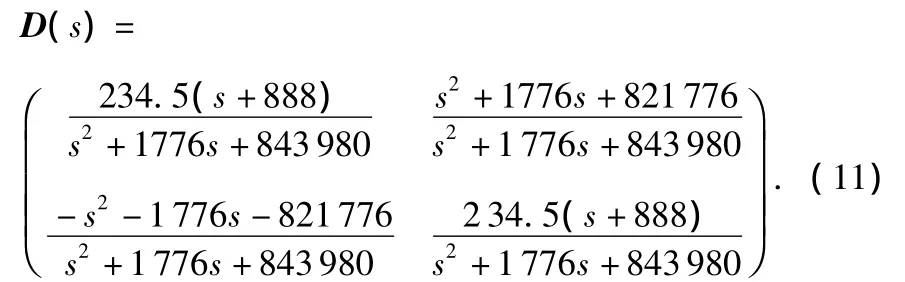
再进一步对式(11)采用零极点近似对消简得到解耦控制网络

3.1 仿真比较

根据国营一四一厂的挠性陀螺仪参数对陀螺仪再平衡控制回路进行仿真，图2、图3分别为再平衡回路不解耦和增加解耦控制网络式(11)的2种情况下，系统X通道的角速率阶跃输入下，挠性陀螺分别在X，Y通道的响应。

图2 X通道阶跃输入无解耦控制时的响应Fig 2 Response of X channel step input without decoupling control

图3 X通道阶跃输入有解耦控制时的响应Fig 3 Response of X channel step input with decoupling control

比较2种情况下的阶跃响应，系统X通道阶跃输入时，不采用解耦控制时，在动态过程中Y通道产生的最大耦合量为140/1100=12.7%;解耦后动态过程中最大耦合量为9/1200=0.75%。由此可见，工程简化的解耦控制算法不仅算法简单易于实现，而且从仿真效果来看，控制算法有效抑制了陀螺仪动态过程中的耦合量，降低了挠性陀螺轴与轴之间的影响，有利于扩大挠性陀螺应用范围。

3.2 试验分析

为了进一步验证解耦控制的效果，对某型挠性陀螺仪进行了试验。常温下，将挠性陀螺仪放在角速率突停台上，平台以ω=10°/s的角速率匀速转动，然后利用转台的起停控制器，平台突然停止，相当于在挠性陀螺仪X轴输入了一个阶跃角速率信号，通过示波器观察在单轴阶跃输入下，挠性陀螺仪在X，Y轴的输出响应。

利用上述试验，可以测试挠性陀螺的动态响应特性。试验中，分别对3只挠性陀螺组件进行测试，X轴角速率由10°/s突停，表1中，给出3只挠性陀螺仪解耦控制前后动态响应效果。

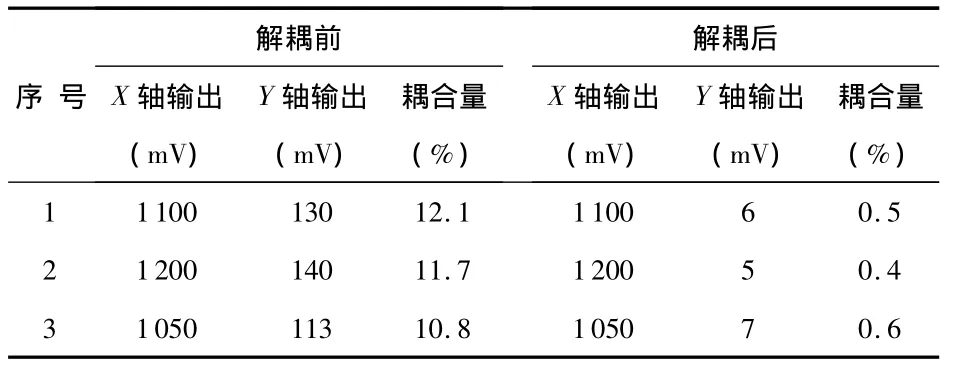
表1 测试结果Tab 1 Test results

表1给出:解耦前3只挠性陀螺仪的最大耦合量为12.1%，增加解耦控制后，3只挠性陀螺仪耦合量都控制在1%以内。试验结果表明:解耦控制有效抑制了挠性陀螺仪的动态过程中的耦合量，成功地解决了配套系统陀螺仪搜索镜头由正转变逆转或由逆转变正转时，俯仰(或方位)向上产生明显的抖动问题，满足了系统要求。

4 结论

本文在建立挠性陀螺仪再平衡回路控制模型基础上，推导出了解耦控制网络的算法，然而再平衡回路一般采用模拟控制，对于复杂的控制网络很难实现，为了简化解耦控制网络，结合陀螺工程实际中的应用，本文忽略陀螺仪传递函数矩阵的二阶项，然后对动态解耦矩阵对消相近的零极点构造出电路上易于实现的解耦控制矩阵。通过仿真验证了解耦控制算法的有效性，最后进行了小批量试验，试验结果表明:解耦控制网络有效抑制了挠性陀螺仪的动态过程中的耦合量，并将耦合量控制在1%以内。

［1］姚军军，任建新，高英俊.挠性陀螺组件模拟再平衡回路的改进与实现［J］.测控技术，2011，30(4):1-4.

［2］戴绍忠，汪 渤.动力调谐陀螺平衡回路的全解耦鲁棒控制［J］.导弹与航天运载技术，2006(4):37-41.

［3］郭海荣，马建辉.双自由度陀螺仪再平衡回路的控制解耦［J］.弹箭与制导学报.2006，26(3):8-9.

［4］周百令.动力调谐陀螺与制造［M］.南京:东南大学出版社，2002.

［5］Zhang Lianchao，Fan Dapeng.Development and current states of rebalance loop technology for dynamically tuned gyro［J］.Missiles and Space Vehicles，2008(1):36-39.

［6］薛定宇.控制系统辅助设计［M］.北京:清华大学出版社，2000.