双轴旋转惯导系统转位误差对导航精度影响研究

吴修振，周绍磊，李瑞涛

(海军航空工程学院控制工程系，山东烟台264001)

0 引言

理想情况下，如果系统的惯性元件只存在漂移误差，根据捷联惯导的原理［1］，旋转式惯导系统(INS)的转位运动不会引起任何的附加误差。然而，实际上惯性元件的标度因数误差和安装误差总是存在，它们可能与转位运动耦合而在系统中引起以外的误差效应。研究表明:理想条件下，恰当的双轴转位方案可以补偿掉惯性元件的漂移误差、安装误差以及非对称标度因数误差。然而，当转位运动存在误差时，双轴旋转INS的误差补偿效果会发生改变，本文通过研究非对称标度因数误差对导航精度的影响机理，仿真分析了转位运动误差与陀螺非对称标度因数误差的耦合误差效应，得出了一些具有实际借鉴意义的结论。

1 陀螺非线性标度因数误差效应分析

1.1 非线性标度因数误差引起的数学平台误差角度

惯性元件的标度因数不可能标定得绝对准确，而且标度因数还可能随着时间、环境等因素而改变，造成了实际系统中总存在着惯性元件的标度因数误差。另外，由于原理、工艺等原因，一般标度因数还存在着正反不对称性，会引起一定的标度因数不对称误差［2］。为简化分析，在单轴旋转的条件下分析陀螺非线性标度因数误差效应，结果可以推广到双轴旋转。

考虑到正反标度因数的不对称性，设3只正交安装的陀螺分别感受到的输入角速度为ω1，ω2，ω3，令

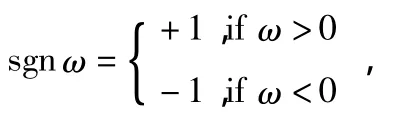
则IMU中3个陀螺的非对称标度因数误差矩阵Sg可表示为

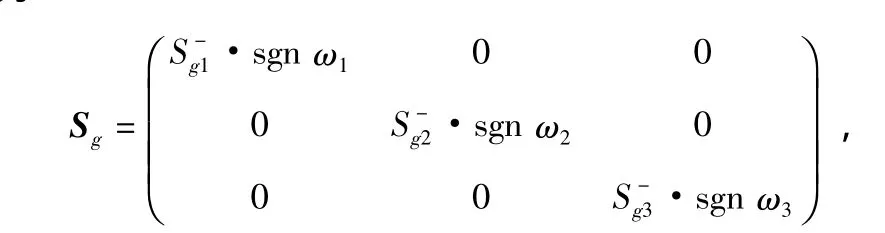
式中 S-gi为第i(i=1，2，3)个陀螺的非对称标度因数误差，亦即为正向标度因数和反向标度因数之差的一半。

导航坐标系采用东北天地理坐标系，并且初始时刻姿态矩阵为单位矩阵，初始时刻的东北天方位和3只陀螺的敏感轴重合，从0时刻开始，控制系统的IMU绕竖直方向以角速度ω开始匀速转动，则可得t时刻的姿态矩阵为

3只陀螺的输入角速度为

其中，ωieN和ωieU分别为地球自转在北向和天向上的分量。

由式(1)，t时刻当3只陀螺输入角速度分别为ω1，ω2，ω3时，IMU机体系中由陀螺的非线性标度因数误差所产生的角速度误差为

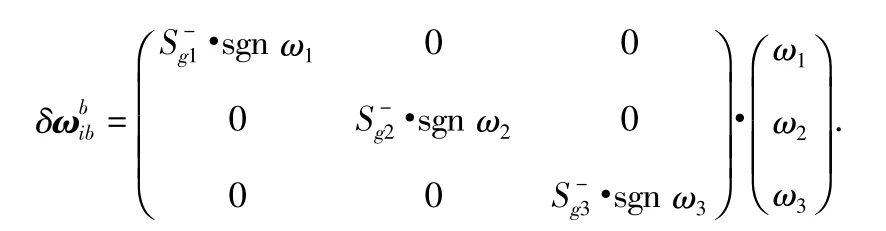
将上面数学平台的角速度误差项在时间T=2π/|ω|内积分，则得到转动一周后数学平台的累积误差角度

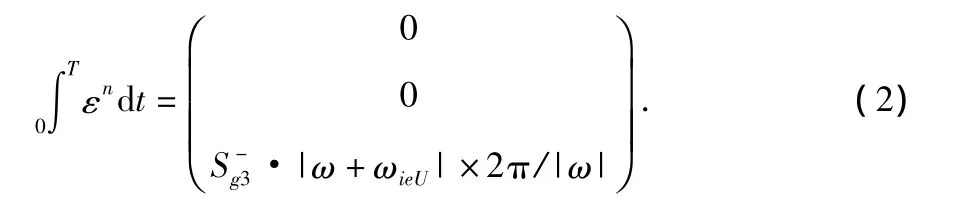
1.2 非对称性标度因数误差的自动补偿效应

根据式(2)的前2个分量可以发现，在旋转运动的一个周期内，与转轴垂直方向上的2只陀螺的标度因数的非对称性误差项S-g1，S-g2消失了，即单轴转动可以平均掉敏感轴与转轴垂直的陀螺的非对称性标度因数误差所引起的导航误差。

将以上结论推广，对于双轴旋转INS，在隔离载体运动的情况下，可以“平均掉”所有惯性元件的非对称性误差效应。上面是在理想境况下得到的结论，如果系统的转轴受控制精度和码盘精度的影响，转动时存在误差，转位误差会和非对称标度因数误差发生耦合作用，最终将可能导致导航误差的积累甚至发散。

2 转位误差与非对称标度因数误差耦合效应分析

对于双轴旋转INS，目前合理的转位方案大致有2种:十六次序和三十二次序［3，4］。通过导航仿真可以发现，两者在对导航误差的抑制方面基本上具有相同的效果，下面针对十六次序转位方案分析转位误差与非对称标度因数误差的耦合效应。

以导航坐标系东北天坐标系xnynzn作为参考，十六次序转位方案是指IMU绕zn轴和xn轴(或者yn轴)以一定的次序顺序转过180°，每一次旋转之间都停留一定的时间ΔT，通过这种不断地转停来消除影响导航精度的误差因素。

单独看绕天向轴zn轴的旋转，共有8次，由于转位误差的存在，每一次旋转时都不能精确地转过180°，为了分析的方便，假设控制转动时不出现超调，那么，每次转位时都会离目标位置xn有一个Δθ的误差角，Δθ相当于转动的死区，转位示意图如图1所示。

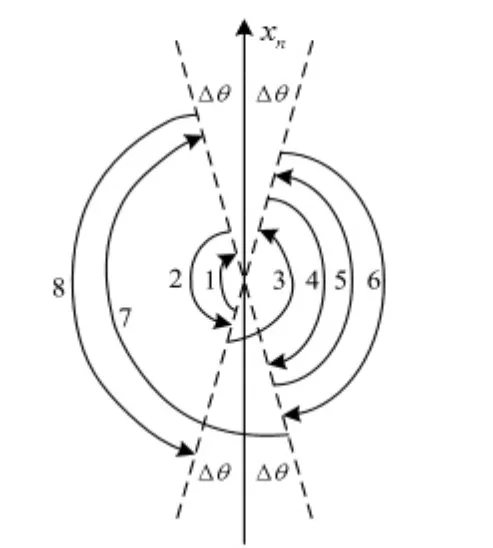
图1 绕zn转动过程图Fig 1 Rotation process around zn axis

由图1可以看出:在3次序和7次序转动过程中，xn轴的负向比xn轴的正向多转过了两次2Δθ，这就造成了等效非线性标度因数误差矢量在转动过程中的空间分布不对称，表现在导航解算中就会等效地引入常值误差，通过积分作用引起导航精度的下降，最终体现在经度位置的发散上。

3 仿真分析

仿真条件设定如下:旋转速度ω=16.7°/s，每个位置停留时间ΔT=10 s，3只陀螺的标度因数不对称性均为S-gi=1×10-6(i=1，2，3)，所处纬度 L=39.8°，所处经度 λ =116.2°，转位周期T=332.8 s，每经过一个周期T存储一次导航数据，导航时间为200 h。当转位误差分别为Δθ=6″，12″，18″，24″时，与 Δθ=0″时的导航经度误差对比图如图2、图3、图4、图5所示。

由图2、图3、图4、图5可以看出:在3只陀螺的非对称性标度因数相同的条件下，导航经度误差会随着转位误差的增大而增大，Δθ=6″，12″，18″，24″时的经度误差分别为Δλ =0.004'，0.008'，0.012'，0.016'，两者近似呈线性关系。

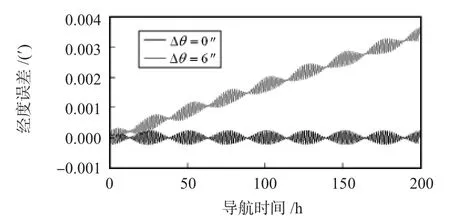
图2 Δθ=6″与Δθ=0″时的导航经度误差对比Fig 2 Navigation longitude error contrast when Δθ=6″and Δθ=0″

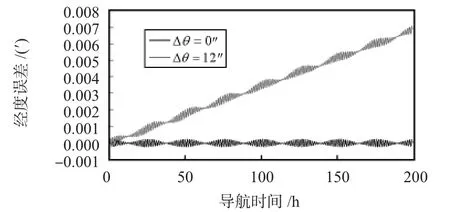
图3 Δθ=12″与Δθ=0″时的导航经度误差对比Fig 3 Navigation longitude error contrast when Δθ=12″and Δθ=0″

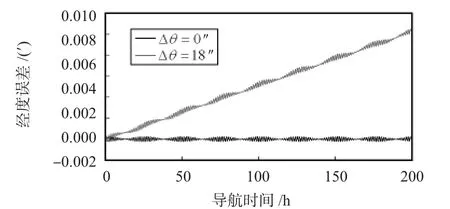
图4 Δθ=18″与Δθ=0″时的导航经度误差对比Fig 4 Navigation longitude error contrast when Δθ=18″and Δθ=0″

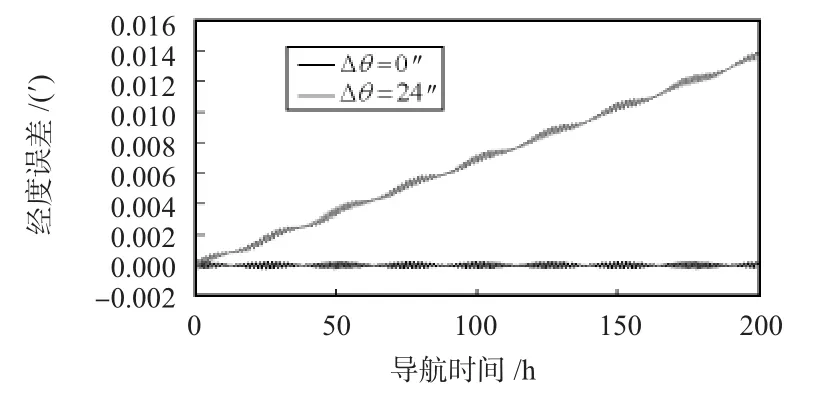
图5 Δθ=24″与Δθ=0″时的导航经度误差对比Fig 5 Navigation longitude error contrast when Δθ=24″and Δθ=0″

若保持转位误差不变，当增大非线性标度因数误差时，最终的导航经度误差会随着非线性标度因数误差的增大而增大。当 S-gi=2 ×10-6(i=1，2，3)，Δθ=24″时，200 h 的导航经度误差会增大到0.03'，如图6所示。

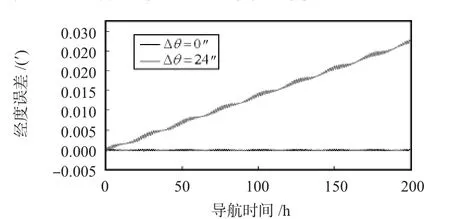
图6 增大非线性标度因数误差后的导航结果对比Fig 6 Navigation results contrast after the nonlinear scale factor error increasing

4 结论

通过以上的分析和仿真过程，可以得出以下结论:双轴旋转INS转位误差会与非线性标度因数误差发生耦合作用，最终影响导航精度，致使导航经度误差的积累和发散，并且两者任何一方的增大都会引起导航经度误差的增大。因此，在设计双轴旋转INS时，要注意选择非线性标度因数误差较小的惯性元件，并且采取措施尽量减小转位误差，提高转位的精确度。

［1］Titterton D H，Weston J L.Strapdown inertial navigation technology［M］.2nd ed.American:Published by the American Institute of Aeronautics and Astronautics and the Institution of Electrical Engineers，2004:231-254.

［2］袁保伦.四频激光陀螺旋转式惯导系统研究［D］.长沙:国防科技大学，2007:26-28.

［3］张 鹏.激光陀螺捷联惯导系统旋转调制技术研究［D］.哈尔滨:哈尔滨工业大学，2010:53-56..

［4］杨 喆.旋转式捷联惯导系统误差分析与转动方案研究［D］.哈尔滨:哈尔滨工业大学，2010:72-76.