分组密码算法矩阵乘法运算的设计原理

张学润, 徐向红, 张学颖

(1. 吉林大学 农学部公共教学中心, 长春 130061; 2. 解放军第230医院 信息科, 辽宁 丹东 118000)

密码算法在军事、 商业等领域应用广泛. 目前, 对密码算法可重构运算架构的研究已取得许多成果[1-3]. 考虑到硬件实现密码算法在速度上的优势及在电路面积、 灵活性方面的限制等因素, 要从根本上提高运算电路的实现性能, 必须对密码算法中的运算进行适当的变换, 使其更适合在密码算法可重构运算电路中运行.

本文结合分组密码算法中矩阵乘法运算的操作特点, 基于比特并行有限域乘法运算方法, 提出全比特并行有限域乘法运算的实现原理； 并利用有限域运算法则, 提出适合分组密码算法中矩阵乘法运算的实现原理. 电路模拟结果显示, 据此原理设计的电路可灵活、 高效地实现不同算法中的矩阵乘法运算, 进而证明了本文设计原理的高可用性.

1 矩阵乘法特征分析

分组密码算法中的矩阵乘法运算就是利用算法给定的乘数矩阵与算法运行过程中的状态矩阵在某个有限域中进行乘法运算, 得到新的状态矩阵. 表1列出了分组密码算法中矩阵乘法的操作特征. 由表1可见, 分组密码算法为提高矩阵乘法的运算速度, 选取维度较小的有限域乘法作为基本运算单元； 同时为使矩阵乘法运算操作数据位宽与密码算法处理数据位宽相匹配, 通常设计维数较大的矩阵乘法运算或多个矩阵乘法运算模块并行运行.

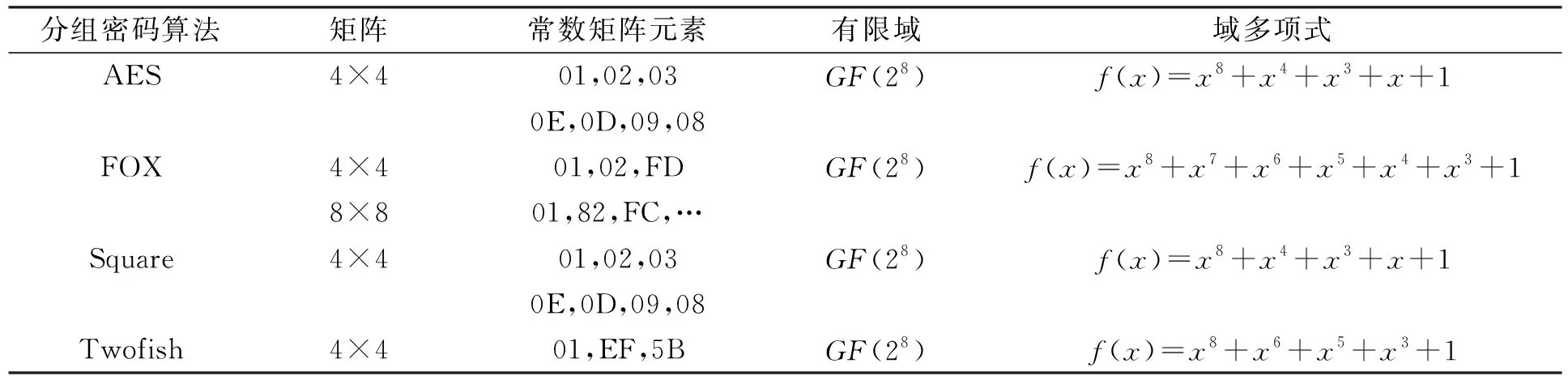
表1 分组密码算法中矩阵乘法的特征Table 1 Characters of matrix multiplicative of block ciphers

2 设计原理

由于不同对称密码算法中矩阵乘法运算的差别主要体现在基本乘法运算所在有限域的生成多项式不同、 乘法矩阵的维数不同两方面, 因此, 矩阵乘法器的实现原理也应从上述两方面考虑.

2.1 全比特并行乘法运算单元

对于维度为k的二元扩域GF(2k), 域多项式f(x)可表示为

f(x)=xk+fk-1xk-1+fk-2xk-2+…+f1x+f0,fi=0,1,i∈[k-1,0];

域中元素：

乘积为

c(α)=a(α)⊗b(α)modf(α)=ck-1αk-1+ck-2αk-2+…+c1α+c0.

结合有限域乘法运算原理, 计算a(α),b(α)的乘积c(α)可分为3步完成：

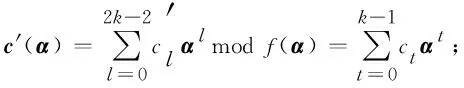
3) 在基域GF(2)中计算乘积项c(α)的系数值.

可见, 二元扩域上的有限域乘法运算均为在二元域上的比特级运算, 可利用简单的“与-异或”电路实现； 运算过程中所需的2k-2次乘积项c′(α)的系数, 可通过密码算法中给出的有限域生成多项式f(x)运算得出.

2.2 2k-2次乘积项系数的运算

对于二元扩域GF(2k)中元素αk+1的坐标可通过元素αk的坐标经过移位、 异或运算得到[4-5], 即

(1)

依次类推, 有限域乘法运算单元中所需的2k-2次乘积项c′(α)的系数均可由初始信息conk计算得出：

即

conk+i=(conk+i-1≪1)+conk+i-1[k-1]·conk,i∈[2k-2,k+1].

(2)

由式(2)可见, 对于二元扩域全有限域乘法运算单元, 只需将域多项式f(x)的系数作为初始值conk, 按上述原理依次生成2k-2次乘积项c′(α)的k-2项系数. 因此, 2k-2次乘积项c′(α)系数的运算同样可由“与-异或”电路实现.

2.3 矩阵乘法运算单元设计原理

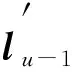
⊗lu-1+…+tu-1,1⊗l1+tu-1,0⊗l0.

(3)

a×bmodf(x)+c×dmodf(x)=(a×b+c×d)modf(x).

(4)

由于对称密码算法同一矩阵乘法中的乘法运算都对应于同一有限域, 因此可利用式(4)给出的有限域运算性质对式(3)进行如下化简：

即对于参与乘积向量元素计算的u个有限域乘法运算, 先对u个多项式乘法运算结果分别进行域多项式约减后再将运算结果相异或运算, 与先将u个多项式乘法运算结果异或运算后再进行域多项式约减的计算结果相同. 基于此, 优化设计矩阵乘法运算电路将极大提升其实现性能.

2.4 矩阵乘法运算单元

由表1可知, 不同对称密码算法中矩阵乘法所在有限域的生成多项式各不相同, 生成多项式的系数也不同, 但运算原理一致, 都是利用有限域生成多项式对域中元素坐标进行变换, 得到运算结果. 矩阵乘法运算电路的结构框图如图1所示.

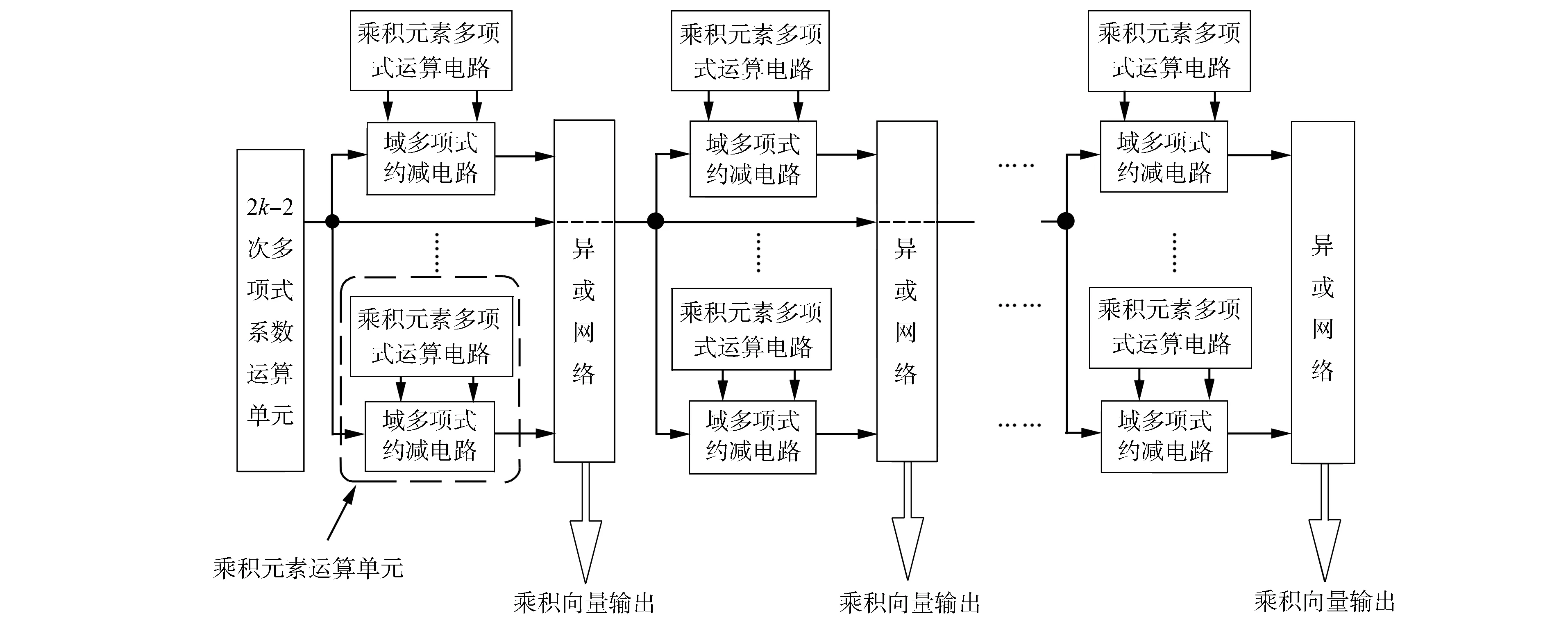
图1 矩阵乘法运算单元框图Fig.1 Architecture for matrix multiplicative

图1中: 2k-2次多项式系数运算电路用于计算多项式约减时所需的系数； 虚线框标识为一个乘积元素运算单元, 用于计算有限域维度较小的乘法运算； 多个乘积元素运算单元通过异或网络计算出乘积向量的一个元素, 并可同时计算多个相同维度的有限域乘法运算. 利用本文给出的原理设计的运算电路可实现表1中所列的分组密码算法中的矩阵乘法运算.

3 结果与讨论

将上述电路结构利用计算机进行模拟, 并将其实现性能与文献中已有方案进行对比, 结果见图2.

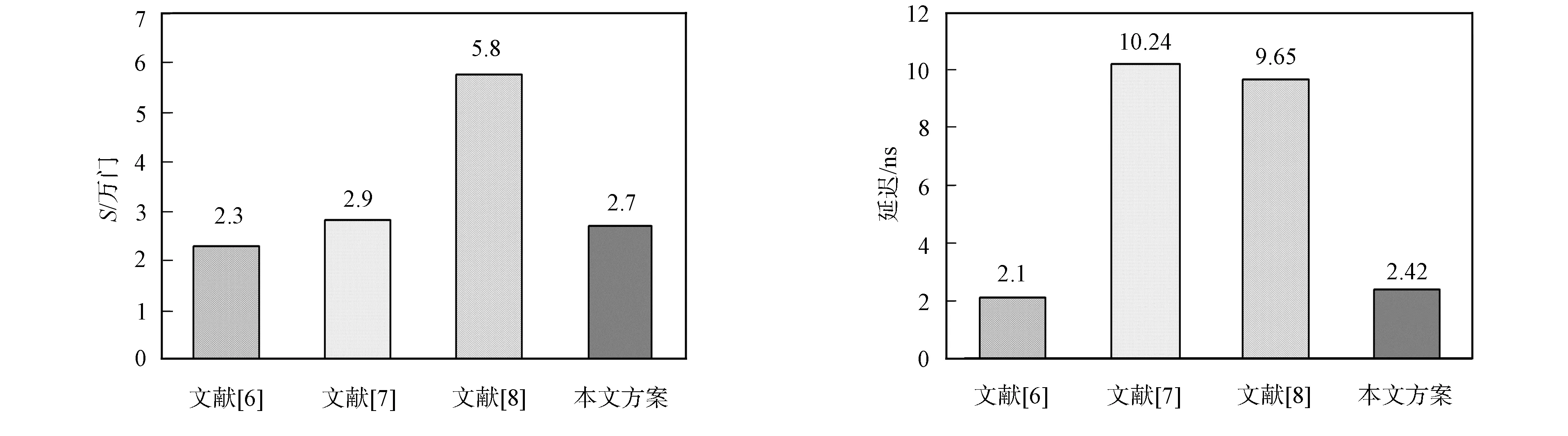
图2 几种不同设计方案的性能比较Fig.2 Performance comparison of matrix multiplicative with other designs

由图2可见: 文献[6]中给出的并行实现方式, 电路面积和运算延迟最小, 只能实现一种算法中的矩阵乘法运算, 利用率不高； 文献[7]利用MSB算法设计的串行乘法运算单元, 电路延迟较大, 不能满足密码算法处理性能的要求； 文献[8]在文献[7]的基础上进行设计, 在减少电路延迟的同时面积增加较多, 但整体运算速度与本文的设计方案相比较慢. 同时, 文献[7-8]中的有限域乘法运算, 将对域多项式系数和操作数坐标的运算同时进行, 应用在矩阵乘法运算电路中时, 无法实现有限域乘法运算间的优化, 虽采用了串行实现方式, 但其电路面积仍比本文提出的设计方案架构大.

[1] QU Ying-jie. Concept and Design Principle of Reconfigurable Cipher Coprocessor [J]. Computer Engineering and Applications, 2003(12): 7-9. (曲英杰. 可重构密码协处理器的概念及其设计原理 [J]. 计算机工程与应用, 2003(12): 7-9.)

[2] YANG Xiao-hui. The Research of Reconfigurable Computing Targeted at Block Cipher Processing [D]: [Master’s Degree Thesis]. Zhengzhou: PLA Information Engineering University, 2007. (杨晓辉. 面向分组密码处理的可重构设计技术研究 [D]: [硕士学位论文]. 郑州: 解放军信息工程大学, 2007.)

[3] LIU Ting-ting. Research on the Structure and Special Instruction-Set of a Reconfigurable Stream Cipher Processing System [D]: [Master’s Degree Thesis]. Zhengzhou: PLA Information Engineering University, 2009. (刘婷婷. 序列密码可重构处理系统结构及专用指令集研究 [D]: [硕士学位论文]. 郑州: 解放军信息工程大学, 2009.)

[4] Berk S, Saras E, Koc C K, et al. Constructing Composite Field Representations for Efficient Conversion [J]. IEEE Transactions on Computers, 2003, 52(11): 1391-1398.

[5] HAN Yong-fei, Leong P C, TAN Peng-chong, et al. Fast Algorithms for Elliptic Curve Cryptosystems over Binary Finite Field in Cryptology [C]//ASLACRYPT’99 Proceedings of the International Conference on the Theory and Applications of Cryptology and Information. London: Springer-Verlag, 1999: 75-85.

[6] Reyhani-Masoleh A, Hasan M A. Low Complexity Bit Parallel Architectures for Polynomial Basis Multiplication overGF(2m)[J]. IEEE Transactions on Computers, 2004, 53(8): 945-959.

[7] Kitsos P, Theodoridis G, Koufopavlou O. An Efficient Reconfigurable Multiplier Architecture for Galois Field [J]. Microelectronics, 2003, 34(1): 975-980.

[8] YUAN Dan-shou, RONG Meng-tian. Reconfigurable and Fast Finite Field Multiplier Architecture [J]. Journal of Eleetronies & Information Technology, 2006, 28(4): 717-720. (袁丹寿, 戎蒙恬. 一种可重构的快速有限域乘法结构 [J]. 电子与信息学报, 2006, 28(4): 717-720.)