用SAS软件实现交叉设计定量资料的统计分析

贾元杰，胡良平＊，程德和

（1.军事医学科学院科技部生物医学统计学咨询中心，北京100850；2.解放军95969部队卫生队，武汉430313）

［本文编辑］阳凌燕

在临床试验中有时会需要让试验因素的两个水平或多个水平先后作用于每一个受试对象，这就需要应用交叉设计。请看下例。

例1 研究两种环孢素微乳化口服溶液在健康人体内的药动学及生物等效性。采用双周期自身交叉对照方案，即将20名受试者按体重随机分为两组，每组10例，在Ⅰ、Ⅱ阶段分别交叉单次口服环孢素微乳化口服溶液供试制剂或参比制剂500mg（5ml），两周期间有一周洗脱期。20名受试者口服500mg环孢素供试制剂和参比制剂后的主要数据见表1［1］。

本例中的一个试验因素是“药物种类”，其两个水平是“A（供试制剂）”和“B（参比制剂）”；观测的定量指标是“血药浓度－时间曲线下面积（AUC0～∞）”。将20名健康受试者随机均分为甲、乙两组，每组10人，用随机的方法决定甲组受试者接受处理的顺序（如先用供试制剂，后用参比制剂），则乙组受试者接受处理的顺序正好相反（即先用参比制剂，后用供试制剂），两周期间有一周洗脱期。此设计是“成组二阶段交叉设计”。

1 交叉设计

1.1 交叉设计的定义和特点［2］在实验中涉及到一个具有两水平的实验因素，根据专业知识的要求，需要该实验因素的两个水平先后作用于同一个受试对象，比较各处理组间差异，综合了自身比较和组间比较的思路。根据实验因素的水平作用的阶段不一样，分为两阶段交叉设计和三阶段交叉设计。（1）若希望实验因素的两个水平在条件相近的同一对受试者中交叉实施，就称为配对二阶段交叉设计；若在两组受试者中交叉实施，就称为成组二阶段交叉设计。二阶段交叉设计，又被称为一次交叉设计或2×2交叉设计。（2）若是希望该实验因素的两个水平A、B要在三个时期作用于同一个受试对象，其顺序要么是ABA、要么是BAB。这两种顺序若在条件相近的同一对受试者中交叉实施，称做配对三阶段交叉设计或配对二次交叉设计；若在两个实验分组中交叉实施，则称做成组三阶段交叉设计或成组二次交叉设计。

交叉设计的特点是：该设计可以考察一个具有两水平的实验因素和两个区组因素（即个体、测定顺序）对观测结果的影响；实验因素的两个水平施加的先后顺序对同一个配对组或两个实验分组的影响是动态平衡的；对于每一受试者而言，均有一个“洗脱期”；在此设计中，实验因素和顺序（或阶段）因素均取两水平，而受试者应取偶数个，以便配对或均分成样本量相等的两个组。交叉设计适用于病情稳定、病程可分阶段的疾病的中、短期临床试验。

1.2 如何合理实施交叉设计 对二阶段交叉设计：（1）应事先选定配对二阶段交叉设计还是成组二阶段交叉设计。（2）若选用配对二阶段交叉设计，先按某些条件将2n个受试对象配成n对，然后，随机地决定每对中一个受试对象接受两种处理的先后顺序，另一个接受处理的顺序正好相反；若选用成组二阶段交叉设计，先将2n个受试对象完全随机地均分成两组，然后随机地决定其中一组受试对象接受两种处理的先后顺序，另一组接受处理的顺序正好相反。

三阶段交叉设计：（1）应选定配对三阶段交叉设计还是成组三阶段交叉设计；（2）若选用配对三阶段交叉设计，先按某些条件将2n个受试对象配成n对，然后随机地决定每对中一个受试对象在3个时期接受两种处理的先后顺序（如ABA），另一个接受处理的顺序正好相反（如BAB）；若选用成组三阶段交叉设计，先将2n个受试对象完全随机地均分成两组，然后随机地决定其中一组受试对象在3个时期接受两种处理的先后顺序（如BAB），另一组接受处理的顺序正好相反（ABA）。

2 实例解析

例2 沿用例1中的资料，试比较A（供试制剂）、B（参比制剂）两种制剂测定结果之间的差别有无统计学意义？

对问题的分析与SAS实现 前面已对此资料中的有关内容做过介绍，一个“药物”因素，具有两个水平，二个区组因素（即重要的非试验因素）“测定顺序”及“受试者”，一个定量指标为“AUC0～∞”。采用二阶段交叉设计定量资料一元方差分析，应用SAS软件实现计算，程序如下：

data a；／＊第1步＊／do ORD＝1to 2；do NO＝1to 20；input MED＄RS＠＠；output；end；end；cards；A 17.54A15.88B20.97A18.51 B 19.94A16.41B17.57A15.87 B 13.94B15.29B15.81A16.11 B 17.42B15.92A14.09A15.95 B 17.00A15.29A16.46B17.86 B 17.17B14.31A19.61B21.56 A 22.14B13.18A17.49B15.15 A 13.49A16.19A15.78B15.14 A 15.95A11.43B16.22B13.93 A 14.02B11.97B14.11A13.27；run；proc ANOVA；／＊第2步＊／Class ORD NO MED；Model RS＝ORD NO MED ORD＊MED；Means MED；ods html；run；proc ANOVA；／＊第3步＊／Class ORD NO MED；Model RS＝ORD NO MED；Means MED；ods html；run；

程序说明：程序第1步通过两个循环语句建立数据集a，其中“ORD”代表“实验顺序”，“NO”代表20个“受试者”，“MED”代表实验因素，“RS”代表“实验结果”。数据流中的“A”和“B”代表实验因素的两个水平，即“A”代表“供试制剂”，“B”代表“参比制剂”。第2步是方差分析，分析实验顺序间、受试者间、药物间及顺序与药物的交互作用。第3步是去掉交互作用后重新对3个主效应进行方差分析。仅当第2步交互作用无意义，进行第3步；否则，不进行第3步。

值得注意的是，在分析交叉设计定量资料时，一般不考察交互作用项。然而，若有需要，交互作用项的效应也是可以考察的。这是因为2×2交叉设计相当于“具有重复实验的2×2拉丁方设计（本例的重复次数为10）”。换句话说，若在k×k（k≥2）拉丁方设计中，做了足够次数重复实验，也可以考察交互作用项的效应是否具有统计学意义。

SAS输出结果及结果解释：

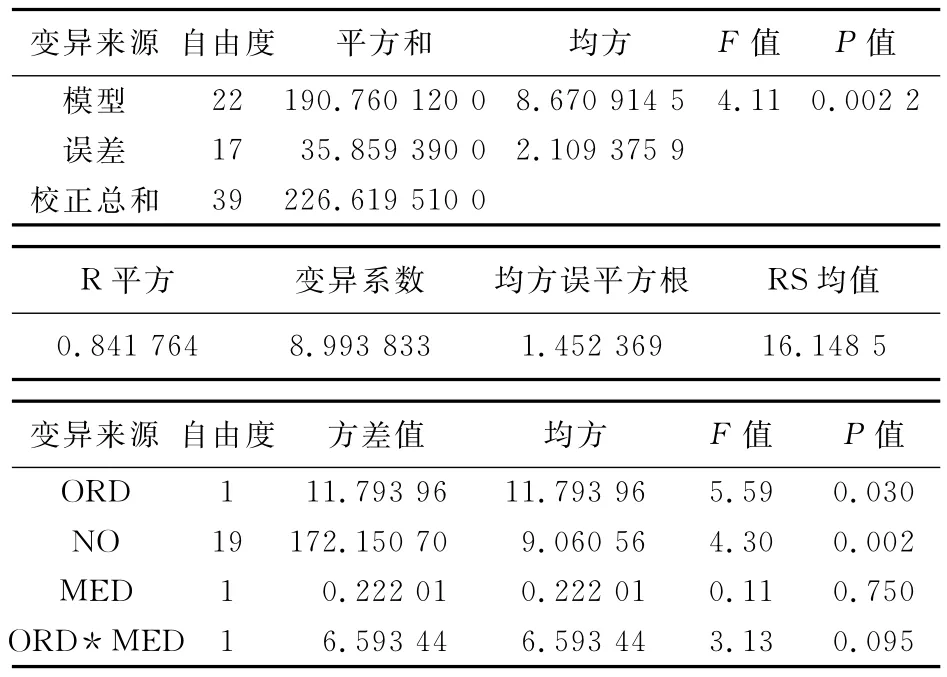
方差分析过程（the ANOVA procedure）因变量（dependent variable：RS）

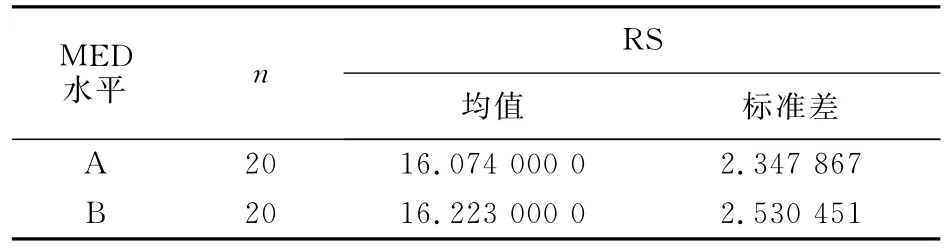
方差分析过程（the ANOVA procedure）

从上面对3个主效应及交互效应的方差分析结果可看出，实验顺序间的差异有统计学意义（F＝5.59，P＝0.030 2＜0.05），受试者间的差异有统计学意义（F＝4.3，P＝0.002＜0.05）。两种药物间、药物与实验顺序间的交互作用的效应均没有统计学意义。进行程序第3步，去掉交互作用，仅分析3个主效应。其结果如下：

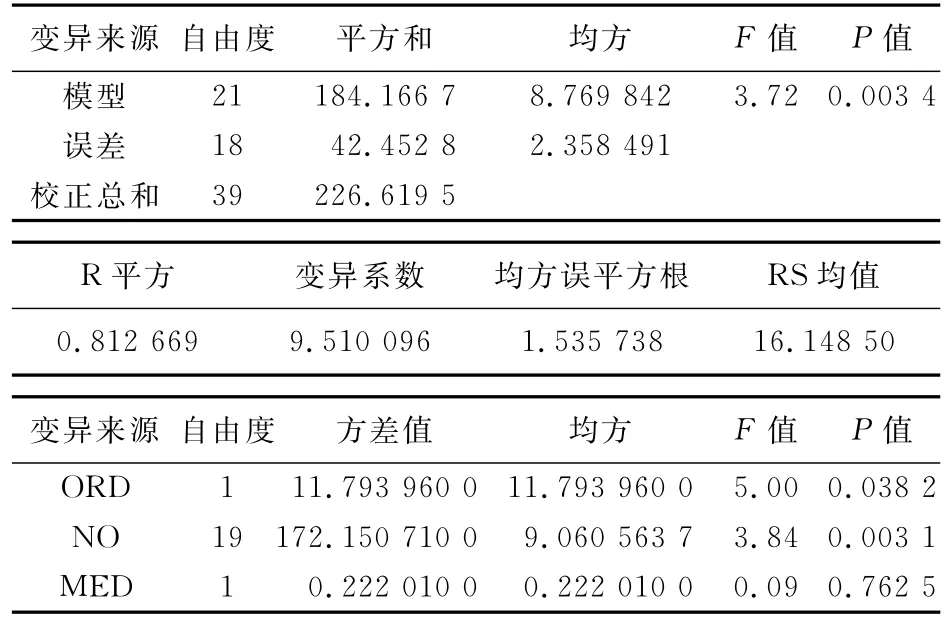
方差分析过程（the ANOVA procedure）因变量（dependent variable：RS）

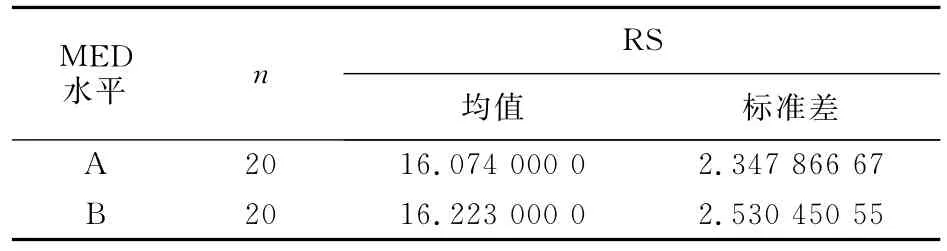
方差分析过程（the ANOVA procedure）

上面的方差分析结果显示，试验顺序间的差异有统计学意义（F＝5.00，P＝0.038 2＜0.05），受试者间的差异有统计学意义（F＝3.84，P＝0.003 1＜0.05），两种药物间的差异没有统计学意义，即供试制剂和参比制剂间差异没有统计学意义。

值得一提的是，研究两种或多种药物作用效果的比较时，以前的统计学教科书和实际工作者常习惯选用交叉设计来安排实验（例如本文引用的文献［1］）。严格地说，这是一个很有质疑的问题！因为同一位受试者先后使用两种或多种药物，后使用的药物的疗效会受到先使用的药物的干扰和影响，但同一种药物在一半受试者身上先用，在另一半受试者身上后用，得到关于该药物作用大小的效应指标的取值是不同质的（更确切地说，药物对结果的影响是非线性的），将不同质的数据简单地求和，再求平均值，采用方差分析在两药物组之间进行比较，本质上是用线性模型来处理非线性数据，其结论的可信度大大下降了。提醒广大实际工作者注意，交叉设计和拉丁方设计一般仅适用于处理因素使观测指标的值不起实质性的改变（如不同秤称量物体的重量），或者仅短暂地间接影响但指标值很快会恢复原状（如不同血压计测血压，心理因素对血压值会有暂时影响）。若处理因素是药物种类，应属于“单个体型交叉设计或拉丁方设计”的禁忌场合，要么采用成组设计或析因设计或其他某种多因素设计，要么采用多个体型（每个个体仅接受一种药物）交叉设计或拉丁方设计。

［1］贺建昌，冯恩富，张 青，等.环孢素微乳化口服液健康人体生物等效性研究［J］.药学服务与研究，2009，9（2）：137－139.He JianChang，Feng EnFu，Zhang Qing，etal.Study on bioequivalence of ciclosporin microemulsion oral solution in healthy volunteers［J］.Pharm Care Res，2009，9（2）：137－139.Chinese with abstract in English.

［2］胡良平.统计学三型理论在实验设计中的应用［M］.北京：人民军医出版社，2006：77.Hu LiangPing.Application of triple－type theory of statistics in experimental design［M］.Beijing：People’s Military Medical Press，2006：77.Chinese.

［3］胡良平.医学统计学：运用三型理论分析定量与定性资料［M］.北京：人民军医出版社，2009：125.Hu LiangPing.Medical statistics：analysis of quantitative and qualitative data with triple－type theory［M］.Beijing：People’s Military Medical Press，2009：125.Chinese.