利用β-二项分布研究新型甲型H1N1流感的聚集性

陈雄飞 董晓梅 陈 希 肖新才 李铁钢 王玉林 王 鸣△

甲型H1N1流感主要为呼吸道传播，其传染途径多数通过患者咳嗽或打喷嚏形成含病毒的空气飞沫，以近距离的传播为主，其发生具有明显的聚集性〔1〕。由于其聚集性，各病例间不具有独立性。大部分的统计分析方法要求病例间具有独立性，如普通的logistic回归分析等，而目前绝大部分文献在研究甲型H1N1流感的时空间分布以及其影响因素时未能考虑聚集性，其结果的准确性有待证实。本研究采用二项分布与β-二项分布模型分析新型H1N1流感在宿舍内的聚集性以及聚集性的强度，为新型甲型H1N1流感的防控以及研究提供参考。

对象与方法

1.研究对象 来自于广州市某中等技术学校2009年8月22日至2009年10月15日新型甲型H1N1流感暴发中的病例，该学校除了个别学生走读外，其余全部为寄宿生。

2.现场流行病学调查与血清学调查 自行设计问卷，暴发终了后对全部学生进行问卷调查。调查内容包括学生的人口学资料、8月20日以来的健康情况、临床症状以及流感发病的相关因素，由经过统一培训后的专业调查人员采取面对面调查与查阅校医门诊记录结合的方式收集。疫情暴发时，按规范要求对自愿者及时采集咽拭子与血清进行检测。该校于10月18日为学生进行年度例行体检，市疾控中心从体检学生的血液样本中分离血清进行血清学检查。

3.新型甲型H1N1流感病例 体温 ≥37.5℃，且咽拭子甲型H1N1核酸阳性或甲型H1N1血凝抑制抗体阳性，伴或不伴有咳嗽、咽痛、流涕等任何临床症状。由于新型甲型H1N1流感为一种新发传染病，在2009年9月前，广州市的监测结果表明人群的感染率＜5%，该校在这之前未发生过流感的暴发流行。暴发调查时，部分病例及对照进行了双份血清抗体检查与咽拭子检查。体检血清抗体阳性病例中，除个别病例外，都有抗体4倍以上升高或核酸阳性，因而可认为抗体阳性者都为本次感染导致。

4.分析方法

(1)使用描述性统计分析一般情况

(2)使用二项分布与β-二项分布拟合新型甲型H1N1流感病例在宿舍间的分布情况，分析其聚集性〔2－4〕。

1)二项分布、β-二项分布及其相关分布:

二项分布:n个独立的是/非试验，其中每次试验的成功概率为p。X表示试验成功的次数，其分布为二项分布。n=1时称为伯努利试验。

超几何分布:有N个样本，其中m个是合格的，在N个样本中无放回地抽出n个，其中X个是合格的概率。如果为有放回则为二项分布。

几何分布:在第n次伯努利试验，才得到第一次成功的机率。即n次伯努利试验，前n-1次皆失败，第n次才成功的机率。X表示试验的次数，其分布为几何分布。

负二项分布:在一连串伯努利试验中，一件事件刚好在第r+k次试验出现第r次的概率。X表示试验的次数，其分布负二项分布。r=1时，负二项分布等于几何分布。

负超几何分布:也称β-二项分布，有N个样本，其中m个为合格的，N-m个为不合格的。每次随机地取出一个样本本，记X为取到r个合格样本的时候所需抽取次数。X的分布就是负超几何分布。当n→∞时，其分布趋向于负二项分布。

二项分布与超几何分布考虑的是成功次数的概率，而负二项分布、几何分布与负超几何分布考虑的是达到固定成功次数所需试验次数的分布。

2)二项分布与β-二项分布特点

二项分布用于描述两种互斥结果的离散型随机事件，具有等概率条件，即事件发生具有相同的概率。β-二项分布是二项分布的推广，属于复合分布，假设二项分布中参数P是一随机变量，且服从β分布，所构成的复合分布即为β-二项分布，主要用于社会中小群体的发病数、小环境内事件发生数的分布模型研究，尤其适用于传染性、遗传度较高的疾病等在家庭、社会中小群体中的聚集性研究〔3〕。其概率函数为:

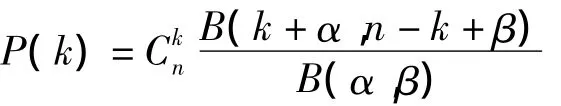
K发生的事件数，α，β为β分布的二个参数。β-二项分布其均数与方差分别为ˉX=nπ与S2=nπ(1－π)(1+nθ)，其中 π =α/(α+β)，θ=1/(α +β)。π 为P的均数，θ为P的方差，由于P具有变异，β-二项分布的方差大于单纯二项分布的方差，θ又被称为聚集系数。由于β-二项分布的方差与二项分布比较相对过大，与其他方差分布过于离散的分布一样，可以计算过度离散系数 φ=1/(α+β+1)=θ/(1+θ)，φ被称为组内相关系数，其值在0～1之间，反映各组内数据的相关程度，即病例在宿舍内的聚集程度，同时也反映不同组之间的相异程度。参数拟合方法有矩法、频数法、最大似然法等。

(3)全部分析采用R 2.12.2软件进行分析，二项分布拟合采用stats模块，β-二项分布拟合采用bbmle模块，参数的估计使用最大似然法。

结 果

1.一般情况

该校有1570个学生，全部为2008级与2009级两个年级的学生，其中新型甲型H1N1流感病例349人，罹患率为22.23%(349/1570)。以宿舍为单位统计各宿舍的总人数与发病人数，因为人数小于3人以及人数多于10人的宿舍数较少，在进行分析时结果不稳定，故分析未利用。将总人数小于3人与总人数大于10的宿舍排除后，共有190间宿舍、1313名学生纳入分析，占全部人数的83.63%，其中有295例病例，占全部分析病例的84.53%，平均每间宿舍6.98人，平均每间宿舍1.54例病例。纳入分析人群罹患率为22.47%(295/1313)，与全部人群比较，差异无统计学意义(χ2=0.023，P=0.878)。不同人口数不同发病人数的宿舍分布见表1。

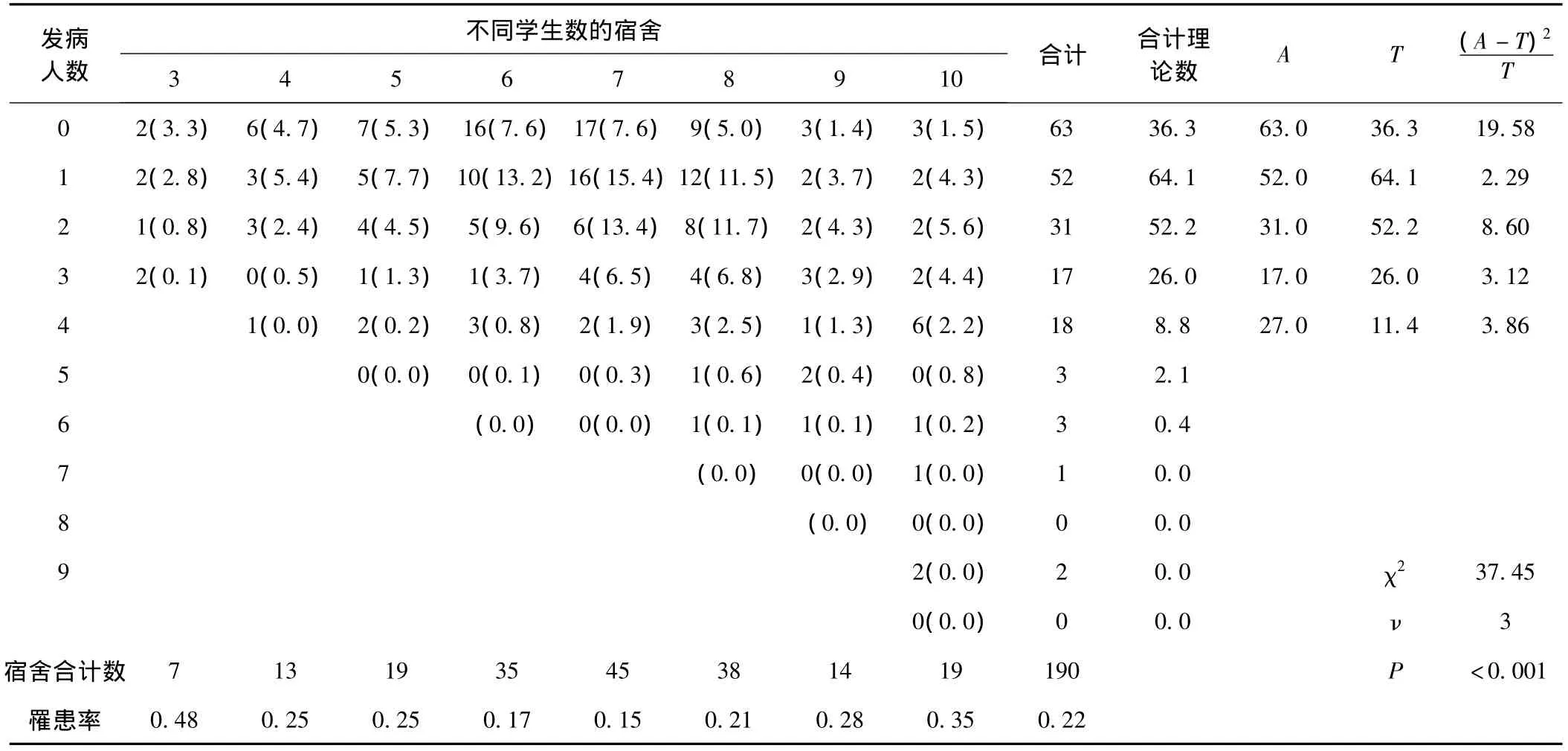
表1 不同学生数的宿舍发病人数的宿舍分布及其二项分布拟合优度检验

2.二项分布拟合优度检验

以22.47%作为罹患率的估计，进行二项分布拟合优度检验，发现本次疫情罹患率的宿舍分布不符合二项分布(χ2=37.45，ν=3，P ＜0.001)。

3.β-二项分布参数估计结果

按宿舍人口数的多少，分别拟合不同人口数下的β-二项分布，结果发现所有人口规模的宿舍的参数π的假设检验均有统计学意义(P全部小于0.01)，各模型所有模型的组内相关系数φ均大于0.75，结果见表2，作散点图发现，从3人到10人的宿舍，其π呈U型曲线，聚集系数与组内相关系数呈钟形曲线，进行相关分析时发现，π与θ呈负相关(r=－0.7，P=0.04)，观察其图形时发现，负指数关系(R2=0.72)可能比线性关系(R2=0.52)更适合。

4.β-二项分布拟合优度检验

以极大似然估计的结果为参数，进行β-二项分布拟合优度检验，发现本次疫情中，宿舍人口数为6～8人的宿舍的罹患率分布符合β-二项分布，结果见表3。其余人口数的宿舍由于人数过少，合并理论数过少的格子后，格子数少于4，导致其自由度小于1，拟合优度检验不能进行。

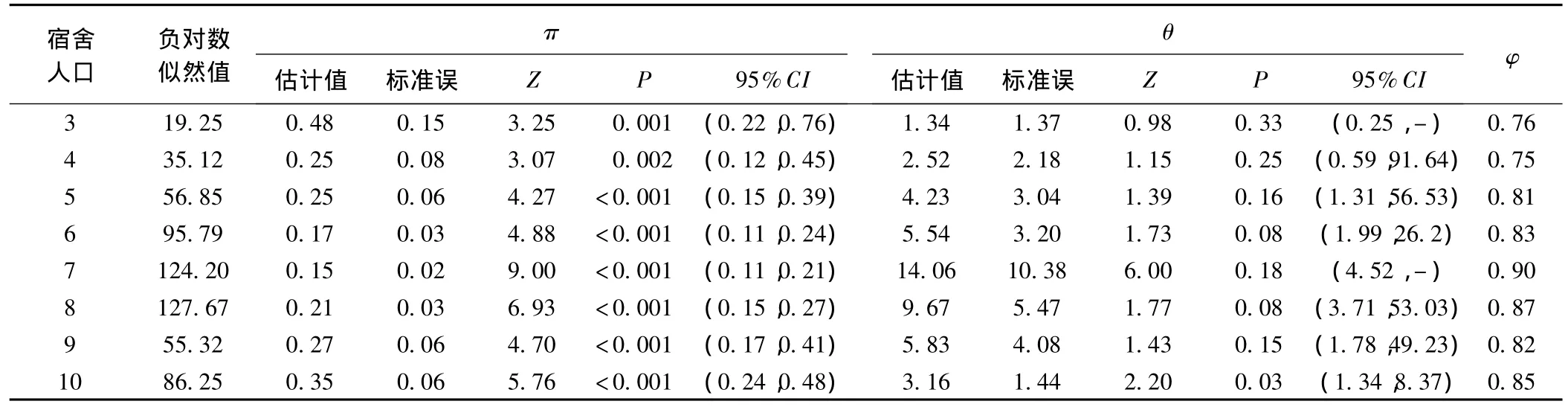
表2 不同人口数宿舍发病人数β-二项分布参数极大似然估计结果

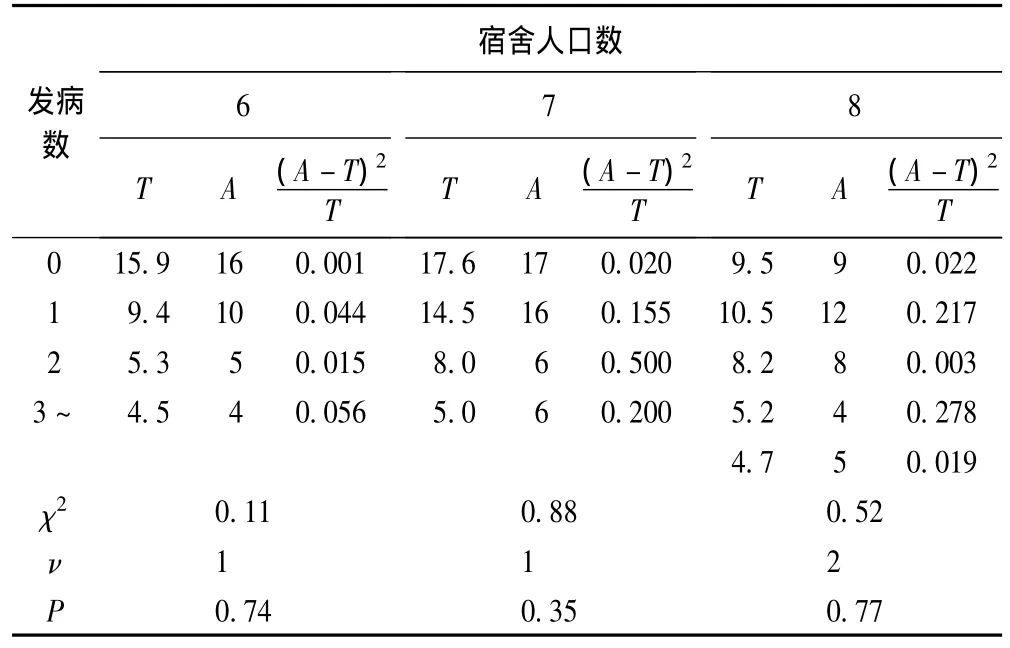
表3 6～8人的宿舍发病人数的β-二项分布拟合优度检验

讨 论

研究者对甲型H1N1流感发生的聚集性已具有共识，但目前国内的文献中均未能对其聚集性进行定量分析，在对影响因素进行分析时，未能考虑聚集性的影响〔5〕，结果的可靠性未能得到保证。一般认为，如果疾病在小单位内无聚集性现象则符合二项分布，并据此判断疾病有无聚集性。如果疾病有聚集性，则根据其性质的不同，研究者用来研究其特点的分布也不同，用的较多的是负二项分布与β-二项分布。本研究中集体单位为宿舍，其发病数不能超过宿舍人数，因而β-二项分布比负二项分布更恰当。本研究采用拟合优度检验发现甲型H1N1流感发病的宿舍分布不符合二项分布，符合β-二项分布，表明本次暴发的甲型H1N1流感宿舍内具有聚集性。β-二项分布的极大似然估计结果发现，所有人口规模的宿舍模型组内相关系数φ均大于0.75，表明各宿舍内的聚集性非常高，组间变异超过了总变异的75%。

由于聚集性分析以集体单位作为样本的个体，而不是以组成集体单位的个人作为个体，因而其有效样本量大大降低。β-二项分布的参数与集体单位的总人数有关，不同人口数的宿舍不能合并进行分析。β-二项分布具有两个参数，在拟合优度检验时，至少有个4理论数大于5的格子才能保证结果的有效性。由于以上条件的限制，本次研究中，拟合优度检验时只对人数为6～8人的宿舍数进行了检验，结果全部符合β-二项分布。

结果显示，(1)不同人数宿舍的聚集系数与组内相关系数均呈钟形，其顶点为7人，提示可能在人口为7人的宿舍中，其聚集性最强;(2)不同人数宿舍的罹患率与人口数呈U型曲线，人口为7人的宿舍罹患率最低，且与3人及10人的宿舍比较，差异有统计学意义(95%CI不重叠)。(3)不同人数宿舍中，聚集性与罹患率呈负相关。该现象可能与不同人口数的宿舍的社交活动特点有关。与其他人口数的宿舍相比，7人宿舍的内部交往最频繁，而宿舍间交往最稀少;因为宿舍间的活动相对较少，不同宿舍间不容易传染;一旦传入，由于宿舍内社交活动频繁，宿舍内传播速度快，而且强度大;由于宿舍间的不容易传染，导致其罹患率低，而由于宿舍内的快速传播导致其高聚集性。以上结果的确切机理需要进一步的专业研究以及利用数理模型进行实证分析与模拟分析。

1．卫生部．甲型H1N1流感诊疗方案(2010年版)

2．罗中云．HBsAg家庭象集性理论概率模式的研究．中国卫生统计，1991，8(3):50-52．

3．陈峰，杨树勤．β-二项分布及其医学应用．中国卫生统计，1996，13(2):10-13．

4．Tripathi RC，Gupta RC，John G．Estimation of parameters in the beta binomial model．Ann Inst Statist Math ，1994，46(2):317-331．

5．陈希，李铁钢，柳洋，等．一起寄宿制学校甲型H1N1流感暴发危险因素分析．中国学校卫生，2011，32(2):208-210．

6．Kreft．I．Are Multilevel Techniques Necessary?http://ioe．ac．uk/multilevel．