基于多层感知器的某矿职工呼吸系统的识别预测*

李 涛

(安徽理工大学理学院 安徽淮南 232001)

由于工作环境的特殊性，导致矿工在工作时不可避免地吸入粉尘。长期吸入粉尘可以导致以肺组织纤维性病变为主的尘肺。目前，尘肺患者肺功能状况是尘肺劳动能力鉴定的重要参考指标之一。此外，暴露于矽尘、香烟烟雾、其它粉尘的肺矽肺矿工也有肺功能障碍超额发生的现象。因此，讨论粉尘对矿工呼吸系统的影响时，要尽可能全面地找出影响矿工呼吸系统的影响因素，才能客观而全面地评价呼气峰流速(pef)为标准的分度法与尘肺病患者的相关性及临床意义，并针对其影响因素进行积极地预防，从而得以提高尘肺病患者的生存质量[1]。由于神经网络具有很好的学习功能，导致该模型具有较好地识别预测功能，所以，笔者将利用人工神经网络(artificial neural networks，ANN)来进行异常数据的识别预测。

1 多层感知器的神经网络的基本概念

1.1 神经网络的基本概念

人工神经网络(artificial neural networks，ANN)系统是20世纪70年代后出现的。它是由众多的神经元可调的连接权值连接而成的，具有大规模并行处理、分布式信息存储、良好的自组织自学能力等特点。这由于神经网络具有这些特点，导致在信息处理、模式识别、智能控制及系统建模等领域得到越来越广泛的应用。尤其误差反向传播算法(Error Back-Propagation Training，简称BP网络)可以逼近任意连续函数，具有很强的非线性映射能力，而且网络的中间层数、各层的处理单元数及网络的学习系数等参数可根据具体情况设定，灵活性很大，所以它在许多应用领域中起到了重要作用。

1.2 多层感知器的概念[2,3]

多层前馈网络是神经网络中的重要一类。这种网络典型地由3部分组成：一组感知单元(源节点)组成输入层，一层或多层计算节点的隐藏层，还有一层计算节点的输出层。输入信号在层层递进基础上前向传播通过网络，这些神经网络通常被称为多层感知器(multilayer perceptrons， MLPS)。在监督学习的方式下使用通称为误差反向传播算法这种非常普遍的算法训练多层感知器，它们已经成功应用于不同的复杂而困难的问题。误差反向传播算法是基于误差修正学习规则的。因此，它可以被看成是同样普遍使用的自适应滤波算法的推广。

基本上，误差反向传播学习由两次经过网络不同层的通过组成：一次前向通过和一次反向通过。在前向通过中，一个活动模式(输入向量)作用于网络感知节点，它的影响经过网络一层接一层地传播，最后，产生一个输出作为网络的实际响应。在前向通过中，网络的突触权值全为固定的。另一方面，在反向通过中，突触权值全部根据误差修正规则来调整。特别是从目标响应减去网络的实际响应的实际响应而产生误差信号。这个误差信号反向传播经过网络，与突触连接方向相反——因此叫“误差反向传播”。突触权值被调整使得网络的实际响应从统计意义上接近目标响应。误差反向传播算法在文献中称为反向传播算法(back-propagation algorithm)，或是简单称为反向传播(back-prop)。

1.3 多层感知器的特点[3-5]

多层感知器有3个突出的特点：

(1)网络中的每个神经元模型包括一个非线性激活函数。满足非线性要求的一个普遍应用形式是由logistic函数：

(1)

定义的sigmoid非线性，其中vj是神经元j的诱导局部域(即所有突触输入的加权和减去偏置)，yj是神经元j的输出。非线性的出现是很重要的，否则网络的输入输出关系会被归结为单层感知器所具有。

(2)网络包括一层或多层隐藏神经元，它们不是网络输入输出的部分。这些隐藏神经元逐步从输入模式(向量)中提取更多的有用特征，可以使网络学习复杂的任务。

(3)网络展示出高度的连接性，它由网络突触决定，网络连接的改变需要突触连接数量或其权值的改变。

正是由上述特性以及通过训练从经验中学习的能力相结合使得多层感知器具有它的计算能力。正因为如此，反向传播算法的发展是神经网络发展史的一个里程碑，因为它为训练多层感知器提供了一个有效的计算方法。

2基于多层感知器的神经网络算法设计

2.1 多层感知器——反向传播算法的设计[6]

神经元j在迭代n时(即呈现第n个训练例子)输出误差信号定义如下：

ej(n)=dj(n)-yj(n)

(2)

(3)

集合C包括网络输出层的所有神经元。

令N记为包含在训练集中模式的总数。对所有n求δ(n)的和然后关于集的大小规整化即得均方差误差能量，表示为：

(4)

误差能量的瞬间值δ(n)和误差能量的平均值δN是网络所有自由参数(即突触权值和偏置水平)的函数。

对下一个给定的训练集，δN表示的代价函数作为学习性能的一个量度。学习过程的目的是调整网络的自由参数使得最小化δN。要达到这种最小化，本文采用了一个训练的简单方法，即权值在一个模式接一个模式的基础更新，直到一个回合(epoch)结束，也就是整个训练集的完全表示已被网络处理。权值的调整根据每个呈现给网络的模式所计算的各自的误差进行。因此，这些单个权值在训练集上的改变的算术平均，是基于使整个训练集的代价函数δN最小化的真实权值改变的一种估计。它是神经元j被它左边的一层神经元产生的一组函数信号所反馈回来的。因此，在神经元j的激活函数输入处产生的诱导局部域vj(n)是：

(5)

m是作用于神经元j的所有输入(不包括偏置)个数。突触权值wji(相当于固定输入y0=y0+1)等于神经元j的偏置bj。所以迭代n时出现在神经元j输出处的函数信号yi(n)为：

yi(n)=φi(vi(n))

(6)

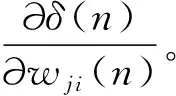
这样，可以得到反向传播算法导出的关系。首先，由神经元i连接到神经元j的突触权值的校正值Vwji(n)由delta规则定义如下：

Δwji(n)=η·δj(n)·yi(n)

(7)

其中：η为学习率参数；δj(n)为局部梯度，取决于神经元j是一个输出节点还是一个隐藏层节点；yi(n)为神经元j输入信号。

2.2 反向传播算法的停止准则

通常情况下，由于不能证明反向传播算法收敛，并且没有明确定义它的停止运行准则。笔者采用的是如下的停止准则：最小点的特殊性质是代价函数或误差量度δN(W)在w=wn的。即是说，当每一个回合的均方误差的变化的绝对速率足够小时，认为反向传播算法已经收敛[6]。均方误差的变化的绝对速率如果每个回合是在0.1%到1之间时，一般认为它足够小。

此外，在每一个学习迭代之后，都要检查网络的泛化性能。当泛化性能是适当的，或泛化性能明显达到峰值时，学习过程被终止[6]。

2.3 反向传播算法的流程[7]

2.3.1 初始化 假设每一先验知识可用利用，以一个随机分别随机挑选突触权值和阀值，这个分布选择为均值等于0的均匀分布，它的方差的选择应该使得神经元的诱导局部域的标准偏差位于sigmoid激活函数的线形部分与饱和过渡处。

2.3.2 训练样本的呈现 呈现训练样本的一个回合给网络，对训练集中以某种形式排序的每个样本，依次进行在下面的第3点和第4点中所描述的前向和方向计算。

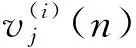
(8)

2.3.4 反向计算 计算网络的δ(即局部梯度)，定义为：

(9)

(5)迭代[7]

通过呈现新的一回合样本给网络，并根据第3点和第4点进行前向和方向迭代计算，直到满足停止准则。

由于训练样本的呈现顺序是从一个回合到另一个回合必须是随机的。动量和学习率参数随着训练迭代次数的增加而调整(通常是减少的)。

3 多层感知器的神经网络算法在计算机中实现

3.1 数据来源

本文是以安徽某地矿业集团从事综采、通风、机电等工种为研究对象，按照国家体育总局制定的《国民体质测定标准手册》[8]，由专业人员在规定时间内在统一器材上对研究对象进行测定，常规医学指标由某市矿业集团职业病防治中心协助测试。

3.2 计算参数

计算时，分区参数是根据个案的相对数量随机分配个案，分区标准如表1所示。

表1 分区参数

体系结构参数如表2。

表2 体系参数

培训类型采用：批处理，优化算法采用调整的共轭梯度，其培训选项见表3。

表3 培训选项

培训错误的最小相对变化为0.0001，培训错误率的最小相对变化为0.001。

3.3 计算结果与分析

按照上面的算法和参数，程序最终运行后，得到模型如图1所示：

训练 平方和错误相对错误中止使用的规则培训时间.387.327错误未减少的 1 连续步骤00∶00∶00.000测试 平方和错误相对错误.00980.409

因变量: 预测值80a. 基于检验样本的错误计算。

图1 模型汇总

可见，神经网络程序已经能正确识别并预测出相关统计数据，程序运行最后得到残差见图2。

因变量：预测值80

从图2看来，程序运行后的结果已经能通过残差检验。

根据上面的计算结果，可以得出下的结论：该神经网络模型能识别预测出可能有6名呼吸道患者，见图3。

N百分比样本 训练测试有效已排除总计382406510595.0%5.0%100.0%

图3 案例处理汇总

根据某市矿业集团职业病防治中心复检，确实存在6名患者存在呼吸道疾病，表明该神经网络模型具有很高的精度。

4 结论

矿工肺功能的损伤程度是职工工伤与职业病致残程度鉴定的重要内容。当前对矿工尘肺病的鉴定与治疗是热点也是难点[9]。本文力图找出峰值呼吸流速(pef)与矿工呼吸系统之间存在的相关关系。实验表明，利用多层感知器构建的神经网络模型，能较好的实现患者的识别预测。但是，由于本文的数据来源集中于一个矿，尚未测试该神经网络模型能否推广到其他矿。

参考文献：

[1]张海英, 张高洪, 伍传仁,等. 煤矿工人呼吸系统的健康状况调查[J]. 应用预防医学, 2007, 8(4):202.

[2]刘伟伟.基于遗传算法的前馈神经网络优化研究[D].兰州：西北民族大学, 2011.14.

[3]戴雪龙.PET探测器神经网络定位方法研究[D].合肥：中国科学技术大学, 2006.87.

[4]Simon haykin著, 叶世伟, 史忠伟译. 神经网络原理(第2版) [M]. 北京：机械工业出版社, 2004.411.

[5]陈飞.人工神经网络和决策树进行数据分类的对比研究[D].大连：大连海事大学, 2005,41.

[6]廉春波.基于相对熵函数准则的BP算法收敛性分析[D].哈尔滨：哈尔滨工程大学, 2007.30.

[7]崔震华.基于神经网络的煤灰结渣特性的研究[D].北京:华北电力大学, 2007.39.

[8]国家体育总局. 国民体质测定标准手册(成人部分)[M]. 北京: 人民体育出版社, 2003.

[9]董琦, 汪永宁, 余初孺. 对煤矿职工体质健康状况的实证研究[J]. 淮南职业技术学院学报, 2009, 9(33):123.