河浜管道管土相互作用及差异沉降分析

黄崇伟，徐一峰，凌建明，童 毅

（1.同济大学 道路与交通工程教育部重点实验室，上海201804，2.上海市城市建设设计研究总院，上海200125）

由于河浜地基与邻接地基之间的差异沉降、埋地管道对地基表面沉降的影响，路基变形不协调导致路面开裂损坏.因此，管土相互作用机理及河浜沉降计算理论的耦合分析技术问题亟待解决.目前，河浜地区地基沉降计算方法主要采用分层总和法，但分层总和法无法综合考虑管道作为夹杂物的情况，因此有必要明确管土相互作用机理，结合分层总和法计算河浜地段夹杂管道的土基顶面沉降.国内外许多学者对管土相互作用进行了大量研究.1910～1950年A Marston等进行了一系列的研究，得出了系统的Marston理论，该理论奠定了管土相互作用机理分析的基础，至今仍在广泛运用并不断发展：例如H.L.White基于压缩环理论、前苏联的Γ.Κ.克来恩［1］和日本下水道协会充分利用“土拱”效应使得Marston理论模型得到了进一步的发展，文献［2－3］利用离心模型试验和现场实测等方法研究了埋管在上、下沉和水平侧动时作用于管道上的土压力及分布；文献［4］利用现场实测和理论模型分析了管土相互作用机理，进一步丰富了Marston土压力计算理论；文献［5］发现Marston公式中的不足，提出土压力计算公式；也有学者运用SAP5 有限元程序对管土相互作用进行数值模拟计算［6］.

为此，本文应用ABAQUS大型有限元软件，分别采用管道防护、地基全处理及不处理3种方案，通过建立存在河浜、管土接触耦合情况下的3D 道面有限元模型，分析不同方案河浜地段管土相互作用机理及协调变形，其结果可为河浜地区管道设计提供技术参考.

1 河浜管土相互作用有限元模拟

1.1 有限元模型及假设

管道轴向方向与路面方向相同，位于路面结构以下距土基顶面3.5m 处.为充分比较河浜管道管土相互作用及差异沉降，假设河浜管土地基处理方式有3种情况，分别为不处理方案（管道正常埋设回填）、管道防护方案（沿管侧轴向布设水泥搅拌桩）和地基加固方案（路基全断面布设搅拌桩）.并构建有限元计算程序，结合分层总和法及管土相互作用相关理论对河浜管道管土相互作用及差异沉降做全面分析.路面结构按结构容重简化为模型附加荷载，简化计算过程如表1所示，构建有限元模型实体工程如图1所示.

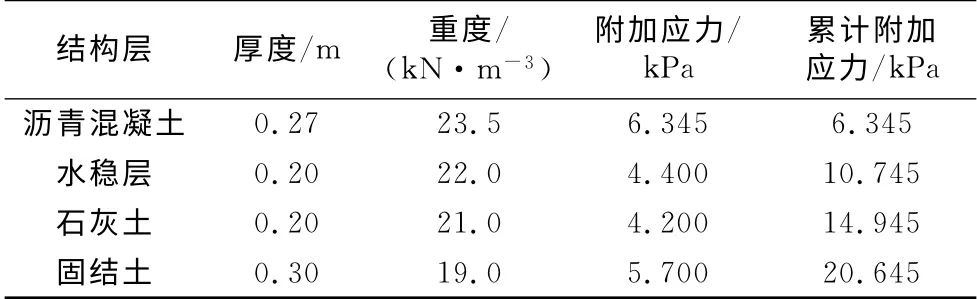
表1 路面结构层参数及附加应力转化Tab.1 Pavement structural and material parameters for additional stress

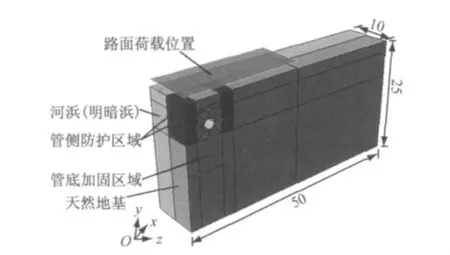
图1 有限元模型（单位：m）Fig.1 FEM model（unit：m）

在现阶段的复合地基设计中主要采用复合模量法计算加固区的沉降，它是将复合地基加固区中增强体和基体2个部分视为复合土体，复合模量Ec取桩、土加权平均值，公式为Ec＝mEp＋（1－m）Es，式中：m为复合地基面积置换率：Ep和Es分别为桩和桩间土的压缩模量.复合土体压缩模量计算见表2.

高大钊［7］、钱家欢［8］、郑颖人等［9］对土体弹性模量、压缩模量及变形模量的关系研究中指出：土体的弹性模量反应土体弹性变形关系，土的变形模量和压缩模量是判断土的压缩性和计算地基压缩变形量的重要指标.为精确模拟管道－土体的协同变形、获得土体管道的弹性和塑性变形，本文有限元计算中采用变形模量作为土体应力应变的本构计算模型.变形模量可通过压缩模量获得：式中：E0为土体变形模量；Es为压缩模量；μ为泊松比.有限元计算材料参数见表3.

表2 复合模量计算过程及计算结果Tab.2 Complex modules calculation process and results

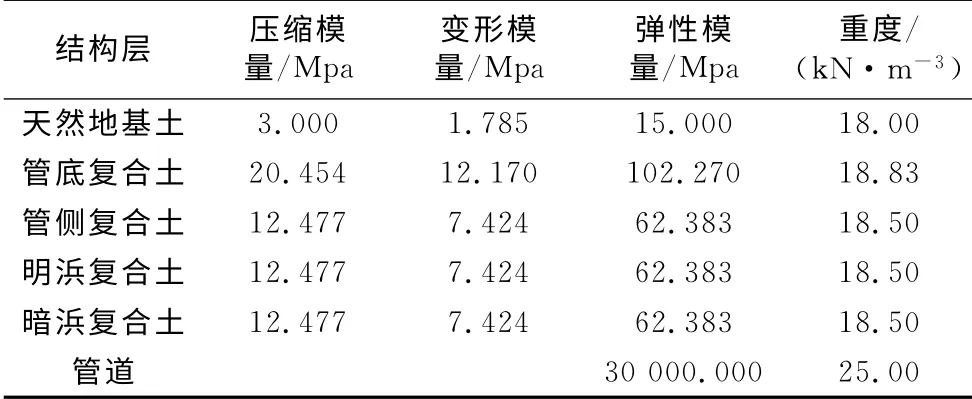
表3 有限元计算材料参数Tab.3 FEM calculation materials parameters

填土与管道之间的摩擦系数定为0.3.为了以较小的计算代价获得较高的计算精度，管道和结构均选取C3D8R 一次插值六面体缩减积分单元，x，z约束各自水平向位移，模型底面（y方向）约束底面竖向位移.图2为明浜管侧单排搅拌桩处理有限元计算云图.

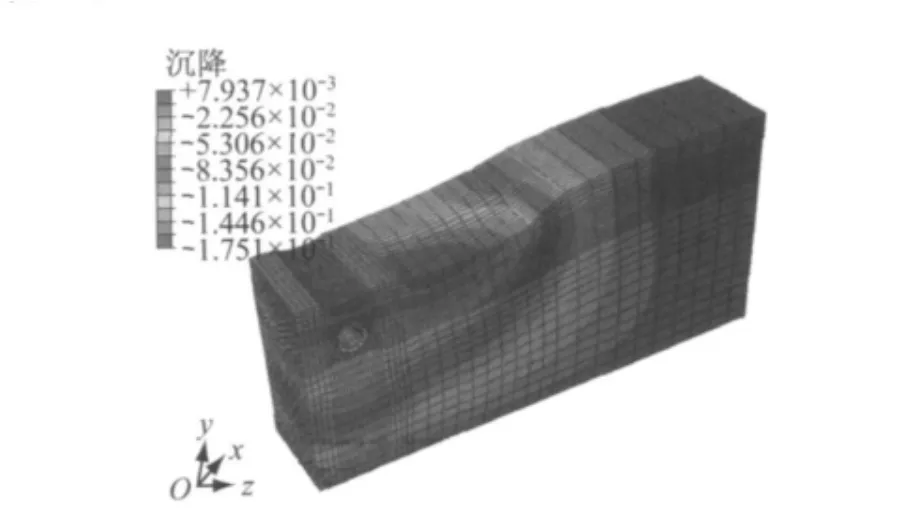
图2 管侧单排搅拌桩处理效果Fig.2 Tube side mixing pile treatment graph

1.2 沟埋式管道Marston及折学森土压力理论

Marston及折学森沟埋式管道土压力模型如图3所示.图中，H为管顶覆土高度；h为沟槽底部与管顶的距离；σx为内土柱微元侧向土压力；σz为内土柱微元上覆竖向土压力；σzH为管顶竖向土压力；D为埋地管道外直径；B为沟槽宽度；z为内土柱埋深.

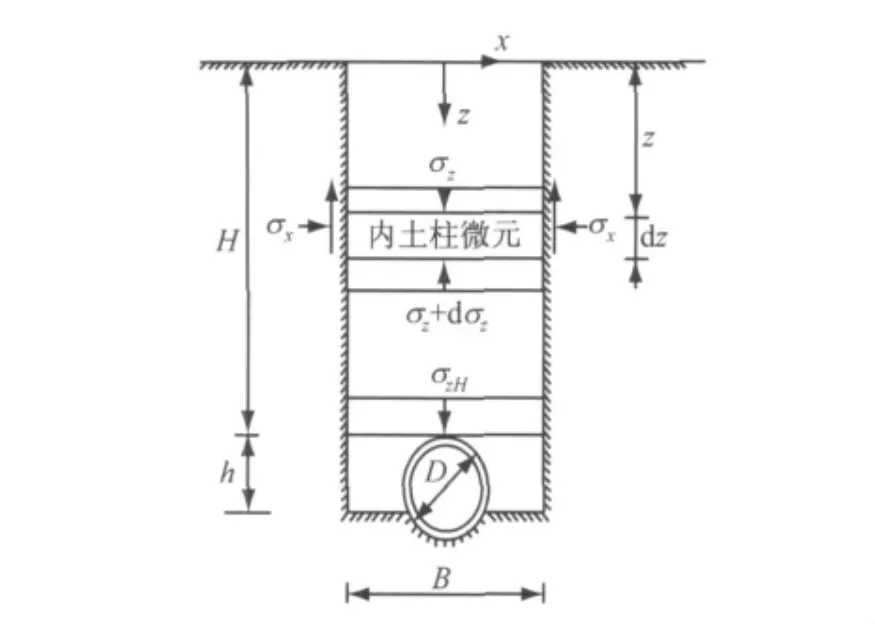
图3 沟埋式管道示意Fig.3 Channel－buried pile schematic diagram

该模型假设：①在沟槽任一深度的平面上，回填土的竖向压力沿全槽宽度均匀分布（即管顶均匀压力分布假定）；②回填土相对槽壁的运动采用极限状态表示（即极限平衡状态假定）；③管顶填土压力全部由管道承担（即管道绝对刚性假定）.通过槽内土柱微元dz的平衡可得沟埋式管道的管顶竖向土压力Fz.

式中：Fz为管顶平面处的竖向土压力；γ为回填土的重度；Kz为管顶竖向土压力集中系数，详细推导过程详见文献［10］.

1.3 河浜土基沉降计算的分层总和法［11］

分层总和法在计算地基沉降变形中的应用已相当成熟，该法一般只用于地基沉降计算.详细计算方法见文献［5－6］.然而，路堤填筑过程是一个逐级加荷的过程，随着填土逐渐增加，各填筑层既是荷载层，又是受压层；同时，由于管道作为路基夹杂物，导致管道土压力计算方法不明.因此本文基于有限元程序计算得管周土压力代入分层总和法计算得管道中心处土基顶面沉降，与有限元计算沉降结果做比较，充分表明本文计算方法的科学.

1.4 模型的验证

运用本文所建立的有限元模型进行计算，模型参数根据文献［12］现场实验工程取值，管顶土体自重应力有限元计算结果、理论解析解计算结果以及现场实验工程检测结果如图4所示［12］.

从图4可以看出，有限元计算结果与实测值较为吻合.一方面，和Marston、折学森计算公式相比，在管顶（深2.4m）处实测值与有限元模拟结果都有土压力集中现象出现，这主要是由于管土刚度相差过大所致，也符合应力刚度分配原则；另一方面，从曲线曲率上看，有限元模拟结果与实测值的曲线形式较为一致.这也从一定程度上表明Marston、折学森计算理论尚待改进.

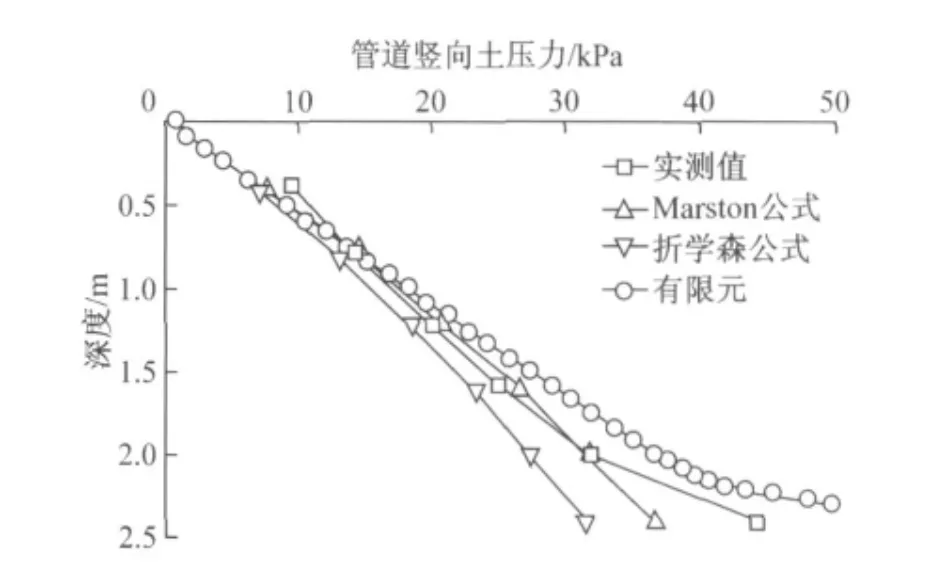
图4 管道土压力实测及计算Fig.4 Channel－buried pile soil pressure calculation

2 河浜管道管土相互作用分析

2.1 河浜管道竖向土压力分析

用分层总和法计算管道顶部土基顶面沉降时常常忽略管土相互作用导致管道沉降计算结果错误.为精确计算管道顶部的沉降，需要对管顶、管底土压力做深入分析.挖槽埋管在板桩起拔时有2种应力集中现象，其一是埋管土压力集中（土压力总量增加），其二是管顶、管底土压力集中.亦即，过去的埋管土压力理论及实用计算公式仅考虑竖向土压力总量，均假设土压力均匀分布，而忽略了管顶、管底处的土压力集中现象，这正是关键问题之所在.

本文运用有限元模型计算得管道中心位置土压力沿深度方向的精确解，如图5，可见：

（1）管顶、管底土压力存在非常明显的应力集中现象.在管顶3.5m 处土压力值高达32.84kPa，在管底6.0m 深处土压力值达到34.01kPa，分别是天然土基同等深处的土压力的2.61和2.99倍.因此，在用分层总和法计算明、暗浜及天然土基顶面沉降时不能忽略管土相对刚度带来的应力集中现象.

（2）按照刚度分配原则，荷载在不同刚度内部会进行应力重分配.与天然土基相比，管底土基使用了长5.0m、间距1.9m、直径0.5m 的水泥搅拌桩加固.相对于天然土基而言，该处符合土压力刚度分配原理，因此在该处应力也相对较大，如图5所示为管道中心处竖向土压力在6.0～12.0 m 深处的变化.

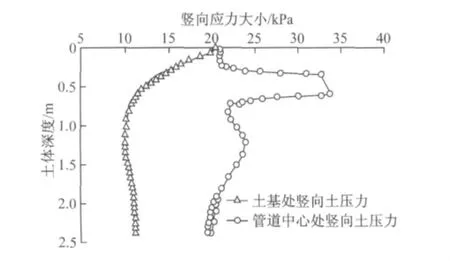
图5 土体竖向附加应力沿埋深的变化Fig.5 Variations of soil additional stress pressure with buried depths

2.2 河浜管道径向土压力分析

通过整理计算结果得到管周土压力分布如图6所示，可见：

（1）土压力最大值出现在管底或者管顶处，对于不处理方案，管道最大径向土压力为43.42kPa；对于管道防护方案，管道最大径向土压力为35.44 kPa；对于路基全断面加固方案，管道最大径向土压力为34.15kPa.显然，在不处理方案条件下管道的径向土压力比管道防护方案的高出22.52%.

（2）管侧位置管道径向土压力等于零，“侧松中实”将极大增加管道的水平径向变形，所以通过该分析可以确定管道周围土体宜采用全路段或水泥搅拌桩侧面加固措施.

图6 不同处理方案的管道径向附加土压力比较Fig.6 Variations of pile radial soil pressure with different treatment schemes

2.3 河浜管道应力分析

分别计算采用管道防护方案、地基加固方案土基处理措施情况下不同位置处的土基顶面差异沉降，计算得管道由附加荷载和重力荷载引起的Mises应力分别如图7所示，由图可见：

（1）3种措施条件下管道结构的最大应力出现在管顶、管侧和管底截面，因此在具体工程设计时只需验算在各种荷载组合条件下管顶、管侧和管底3 个控制截面上的应力能否满足要求即可.

（2）较土体自重应力而言，附加荷载引起的管道Mises应力相对较小，但两者的叠加不容忽视，最大叠加量出现在管侧不处理方案的管顶位置，为4.887 MPa，比管侧2种处理方案高出约12%.从管道自身结构安全来看，管侧土基宜进行加固处理以防止管道本身因受力过大而破坏.

图7 不同处理方案的管道外壁Mises应力Fig.7 Variations of pile Mises with different treatment scheme by gravity

3 河浜管道差异沉降分析

3.1 河浜管道轴向差异沉降比较

土基的不均匀沉降也可能导致管道的不均匀变形，可能造成管道错口、断裂、渗漏等现象.工程设计中对土基轴向差异沉降的要求极高，每2 m 的容许误差为1cm，满足管道设计时“零渗漏”的要求.

假设用5m 的水泥搅拌桩处理管道底部土体，并在管道基底用水泥板承台处理，目的是为了防止管道的差异沉降.从理论计算角度而言，管道轴向可能在明浜、暗浜交界处有差异沉降，为此，分别建立明浜、暗浜模型，在管道轴向的土基顶面取沉降值，由图8可见，管道轴向位置差异沉降极小，管道轴向10m 范围内的土基顶面差异沉降仅约2 mm，满足工程设计要求.

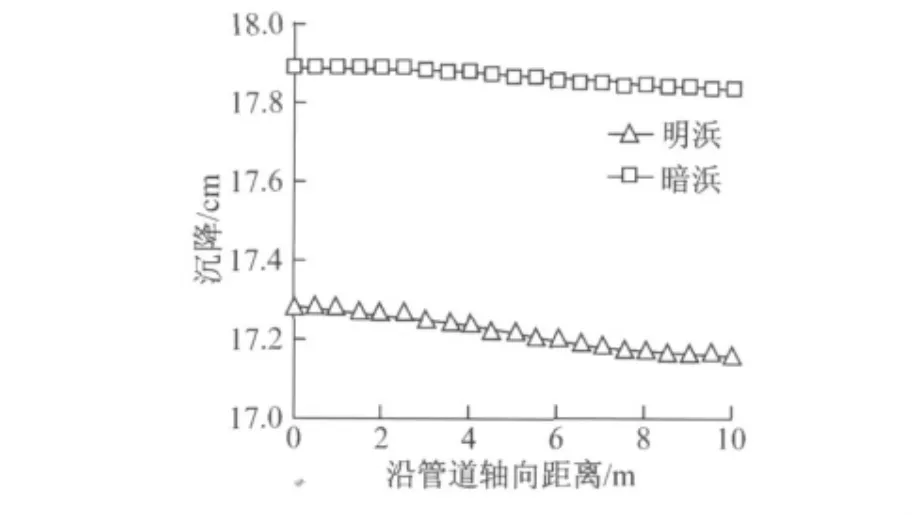
图8 管道轴向土基顶面沉降Fig.8 Pile axial direction settlement on the top of subgrade

3.2 河浜管道横截面方向沉降分析

取距管道中心处一个直径长度的土体范围，分析管道及管道底面基础加固对土基顶面、管顶顶面土体沉降的影响，作出管道横截面方向的管侧土体差异沉降如图9所示.

图9 沿管道横截面方向的沉降Fig.9 Pile transverse direction settlement

（1）在土基顶面位置，采用管道防护处理方案得到的管道中心处沉降为17.27cm，在管侧壁位置土基顶面沉降为16.95cm，两者在1.25m 的范围内差异沉降为3.15mm；采用地基加固处理方案得到的管道中心处土基顶面沉降为17.36cm，在管道侧面土基沉降为17.11cm，两者在1.25m 的范围内差异沉降为2.45mm.因此可见，在管道直径范围内的土基顶面差异沉降满足工程现场的要求.

（2）在管道顶面的土体，采用管道防护处理方案得到的管道中心处沉降为15.82cm，在管侧壁位置土基顶面沉降为15.61cm，两者在1.25m 的范围内差异沉降为2.15mm；采用地基加固处理方案得到的管道中心处土基顶面沉降为15.41cm，在管道侧面土基沉降为15.32cm，两者在1.25m 的范围内差异沉降为0.9mm.因此可见，在管道直径范围内管道顶面土体差异沉降满足工程现场要求.

3.3 河浜管道中心及天然土基差异沉降比较

将有限元计算得出的土体竖向应力作为分层总和法的压缩应力分别计算管道中心处及天然土基处土体沉降，并将计算结果和有限元计算得出的沉降进行对比，如图10.

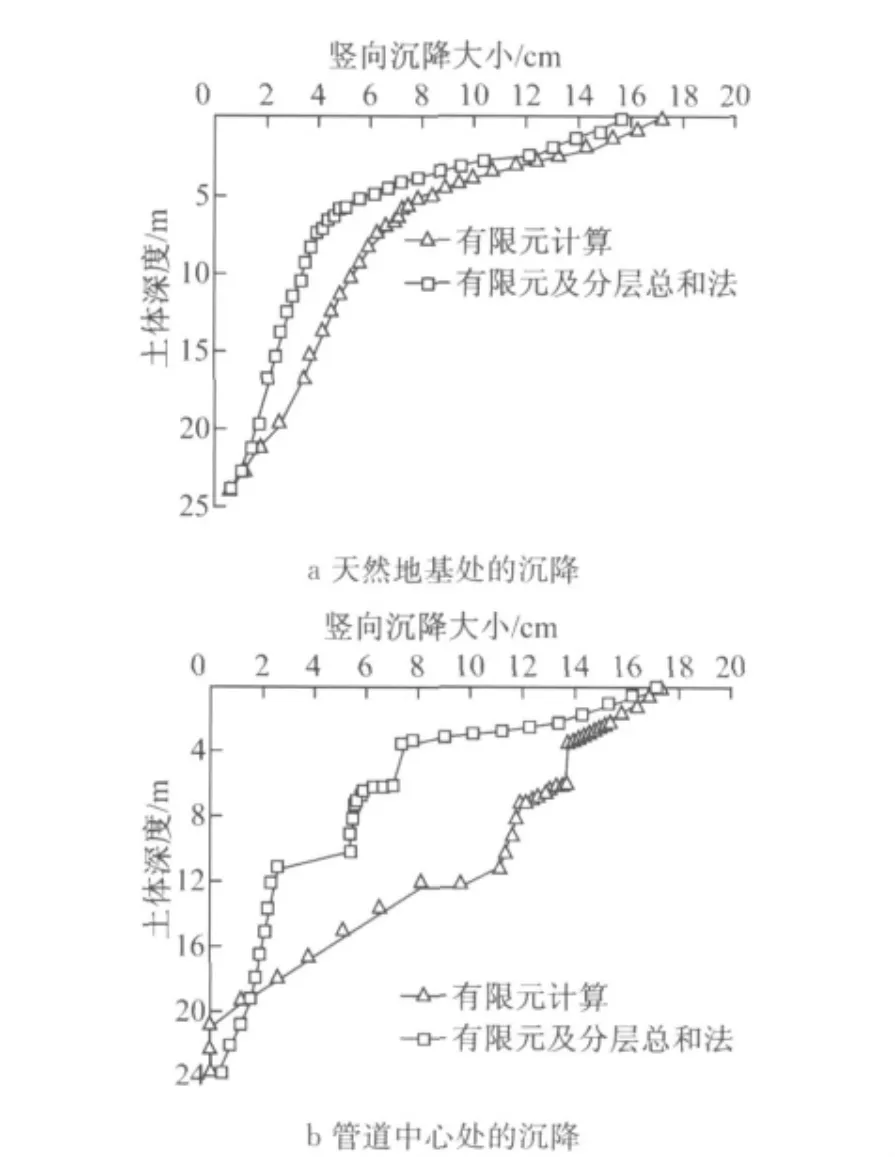
图10 不同方法计算沉降比较Fig.10 Settlement comparison with different treatment schemes

（1）从图10a可见，在天然土基处，将有限元计算得土体竖向压应力代入分层总和法计算各层土体沉降曲线与有限元计算得到的土体沉降曲线较为吻合，因此结合运用分层总和法与有限元法能精确地模拟土体沉降.

（2）从图10b可见，将有限元计算竖向应力代入分层总和法后计算得的沉降在3.5～11.0m 处存在沉降差异，这一则由于管道本身的沉降较小，再则由于管土相互作用使管周土压力存在应力集中现象，三则由于管道土基加固措施使该处土体应力存在分布不均匀现象（如图4）.因此运用分层总和法计算该处土体的沉降存在结果失真现象，有限元计算方法能较好地考虑管土相互作用，得到较为合理的沉降计算结果.

4 结论

（1）管道结构最大应力出现在管顶、管侧和管底截面，因此在具体设计时只需验算在各种荷载组合条件下管顶、管侧和管底3个控制截面上的应力能否满足要求即可.

（2）附加荷载和土体自重荷载引起的管道Mises应力不容忽视，最大叠加量出现在土基不处理方案时管顶位置，达到4.887 MPa，比管侧防护和地基加固2种处理方案高出约12%.因此，管侧土基宜进行防护处理，防止管道本身因受力过大而破坏.

（3）有限元计算结果表明，在管顶（底）处存在由于管土相对刚度差异带来的土压力集中现象，其值分别是天然土基同等深处的土压力的2.61和2.99倍，利用分层总和法计算的沉降也有相同倍数的差异.因此利用传统分层总和法计算管顶中心处土基沉降时势必存在沉降计算结果失真现象，有限元计算方法能较好地考虑管土相互作用因素，计算结果与实际情况较为吻合.

［1］ ГККлейн.地下管道计算［M］.北京：中国工业出版社，1964.ГК Клейн.Underground pile calculation［M］.Beijing：China Industry Press，1964.

［2］ 刘全林，杨敏.上埋式管道上坚向土压力计算的探讨［J］.岩土力学，2001，22（2）：214.LIU Quanlin，YANG Min.Study of vertical soil pressure on positive buried pipeline［J］.Rock and Soil Mechanics，2001，22（2）：214.

［3］ Charles H Trautmann，Thomas D O’Rourke.Lateral forcedisplacement response of buried pipe ［J］.Journal of Geotechnical Engineering，1985，111（9）：1077.

［4］ Itzhak Shmulevich，Naftali Galili，Amnon Foux.Soil stress distribution around buried pipes ［J］. Journal of Transportation Engineering，1986（5），112：481.

［5］ 曾国熙.土坝下涵管竖向土压力的计算［J］.浙江大学学报，1960（1）：79.ZENG Guoxi.Earth vertical pressure coefficient of pipeline in dam［J］.Journal of Zhejiang University，1960（1）：79.

［6］ 苏庆东，苏秋菊，金锋，等.钢筋混凝土圆管应力状态研究［J］.特种结构，1987（12）：426.SU Qingdong，SU Qiuju，JIN Feng，et al.Stress state of reinforced concrete pipe［J］.Special Structure，1987（12）：426.

［7］ 高大钊.土质学与土力学［M］.北京：人民交通出版社，1979.GAO Dazhao.Soil mechanics and soil science［M］.Beijing：China Communications Press，1979.

［8］ 钱家欢.土力学及地基工程［M］.北京：水利电力出版社，1983.QIaN Jiahuan.Soil mechanics and foundation engineering［M］.Beijing：Water Resources and Electric Power Press，1983.

［9］ 郑颖人，孔亮，龚晓南，等.岩土塑性力学原理［M］.北京：人民交通出版社，1978.ZHENG Yingren，KONG Liang，GONG Xiaonan，et al.The principles of geotechnical plastic mechanics［M］.Beijing：China Communications Press，1978.

［10］ 顾安全.上埋式管道及涵洞垂直土压力的研究［J］.岩土工程学报，1981，3（1）：3.GU Anquan.Earth vertical pressure coefficient of positive buried pipeline and culvert ［J］. Chinese Journal of Geotechnical Engineering，1981，3（1）：3.

［11］ 郑治.路堤自身压缩的分层总和法［J］.华东公路，1996，5：51.ZHENG Zhi.Layer－wise summation in embankment［J］.East China Highway，1996，5：51.

［12］ 黄崇伟.机坪输油管道力学行为研究［D］.上海：同济大学交通运输工程学院，2011.HUANG Chongwei.Mechanics simulation and calculation methodology of apron oil pipeline［D］.Shanghai：College of Transportation Engineering of Tongji University，2011.