邻近地上结构对地下结构动力响应的影响参数

王淮峰，楼梦麟，陈 希，翟永梅

（1.同济大学 土木工程防灾重点实验室，上海200092；2.同济大学 土木工程学院，上海200092；3.同济大学 上海防灾救灾研究所，上海200092）

地铁工程是城市生命线的重要组成部分.高烈度地震区内的城市地铁大规模建设是在近20多年才出现的，大多数还没有经过大地震的检验.因此，地铁工程的抗震问题不容忽视［1］.

为了交通方便，地铁车站大都选在繁华商业区、场馆聚集区以及居民住宅小区附近，地铁车站的附近多存在已经建成的建筑.因此，对于地下车站而言，考虑邻近既有地上结构对其地震反应的影响十分必要.以往的研究大多以土 结构相互作用（soilstructure interaction，SSI）理论为基础，仅将地铁车站及其周围的土体作为系统进行研究［2－3］.

结构－土－结构相互作用（structure－soil－structure interaction，SSSI）是近40年来提出的研究课题，属于SSI问题的一个分支领域，它研究在外加荷载或者地震激励下相邻结构物之间的动力反应.随着SSI研究内容的日趋深入，各种研究SSI问题的实验手段和理论方法被用于分析SSSI问题，极大地促进了这一研究领域的发展.但是，已有的工作主要集中于对地上结构物之间相互作用的研究［4－5］，少数学者对地下隧道之间的相互影响进行了研究［6－9］，而对邻近地上结构物对地铁地下结构的影响则研究甚少［10］.

关于SSSI效应产生的机理已经有了一定的认识：从振动方面考虑，相邻结构的存在改变了整个相互作用系统的频率，从而影响了结构的动力响应；从波动方面考虑，地震波在结构间的反射导致了结构动力响应的改变.但对于SSSI效应影响参数的研究甚少.本文利用ANSYS有限元程序建立了一系列典型高层框架结构及地下车站的二维平面应变模型，研究了地震作用下地上结构对地下结构动力响应的影响参数.

1 计算模型及相关参数

选用平面应变单元和二维梁单元分别模拟土层和结构，建立了地上结构－土－地下结构的计算模型，如图1.网格划分的大小对于土－结构动力相互作用问题的计算非常重要，本文按1／8最小波长为限值来划分有限元网格.同时建立地上结构－土层的模型及地下结构－土层的模型以作比较.地铁车站上层层顶距地表2m，上层的层高为6m，下层的层高为8 m，侧墙和中间2 排柱为等间距，均为8 m.梁截面0.40m×1.00m，柱截面0.75m×0.75m.地上结构为框架结构，楼层数N＝12 层，层高3.6 m，宽20.0m；基础为箱型基础，埋深H＝3.5 m.梁截面0.25m×0.60m，柱截面0.60m×0.60m.混凝土强度等级均为C30.

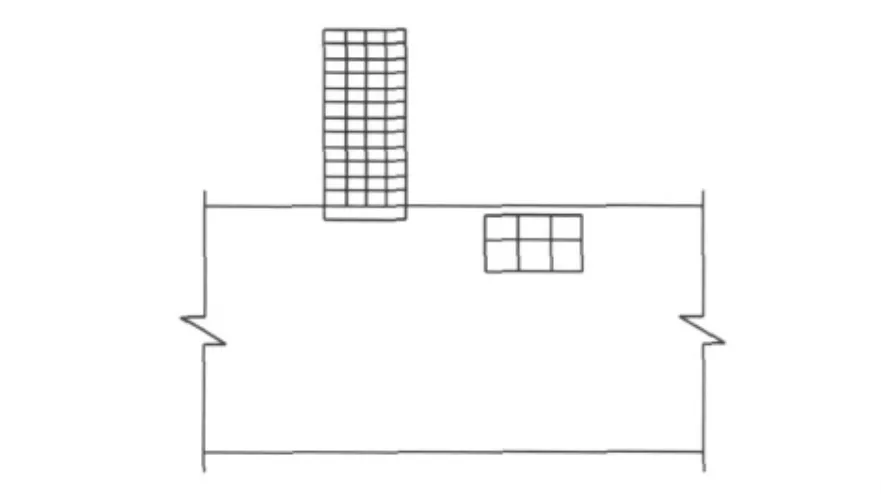
图1 地上结构－土层－地下结构模型Fig.1 Model of superstructure－soil－infrastructure

场地土层采用北京市某处的土层资料，相关参数见表1.将地下60m 处的卵石层顶作为输入地震动的基岩面.地震动输入为竖直向上传播的剪切波（正弦波、实测及人工地震波，见表2、图2）.根据文献［11］的研究，土层范围分别取正弦波激振时20倍土层厚度及地震波激振时12倍土层厚度.作为初步研究，土层及结构采用有阻尼情况下的线弹性模型，阻尼特性采用滞后阻尼模型［12］，阻尼比ξ＝0.05.

采用地铁车站顶板和底板的相对水平位移Ux来衡量地铁车站的动力响应大小，正弦波激振下采用稳定值，地震波激振下采用峰值.以Ux的相对值e来衡量结构间的相互作用.

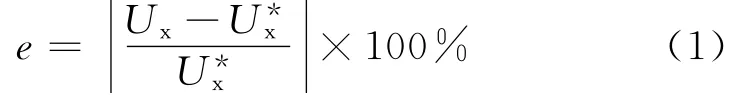
式中，Ux，U＊x分别为地上结构－土层－地下结构系统及地下结构－土层系统地铁车站顶板和底板的相对水平位移.

表1 土层资料Tab.1 Data of subsoil

表2 地震波资料Tab.2 Data of seismic waves

地上结构和地下结构的相对水平位置以量纲一化参数D＝W／B表示，其中，W为2个结构之间的净距；B为地上结构的宽度.以D＝0表示单独地下结构－土层模型.

2 数值分析结果

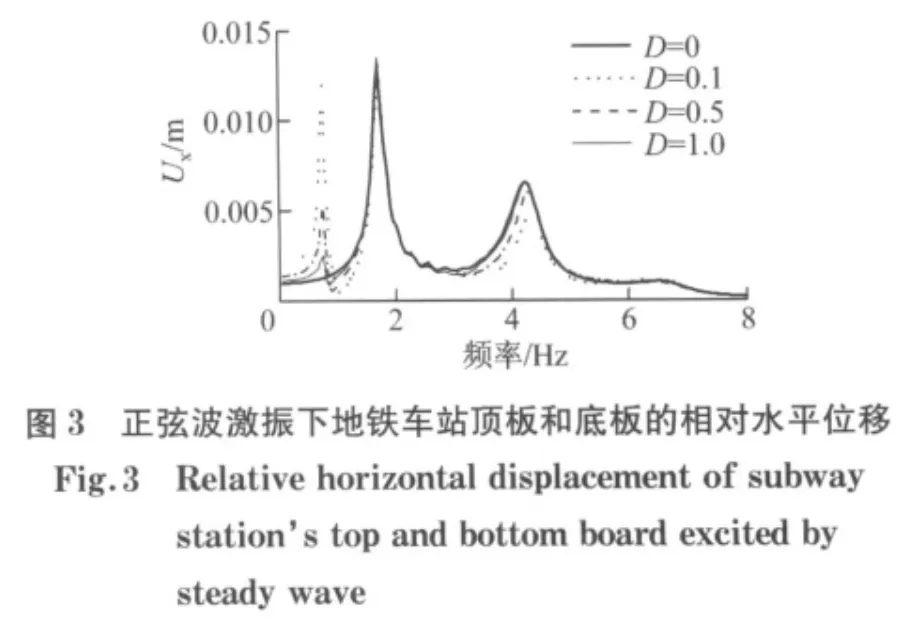
图3为0～8Hz正弦波激振下地铁车站顶板和底板相对位移的稳定值.单独地下结构－土层系统的水平向前3阶自振频率分别为1.70，4.30，6.50Hz.显然，由于地上结构的存在，地下结构的水平地震响应产生了较大的改变.同时，地下结构的2阶频率及3阶频率稍有偏移.地下结构的1，2阶反应有所减小（D＝0.1时，1 阶反应降低了8%，2 阶反应降低了28%），但3阶反应有所增加（D＝0.1时，3阶反应增加了16%）.在地上结构－土层系统的1阶频率（0.75 Hz）附近，位移曲线产生了一个较大的尖点.在0.75 Hz正弦波激振下，当D＝0.1 时，Ux值提高了近1个数量级，即地上结构发生共振极大影响邻近的地下结构，这应引起重视.

图4为3条地震波激振下相对值随结构间距的变化曲线.地震波频谱成分的差异导致了相对值的不同.当D＝0.1时，在P0214地震波激振下相对值可达23%.当D﹥1.0时，地上结构对地下结构地震动力响应的影响基本趋于零.

2.1 土层剪切模量及阻尼的影响

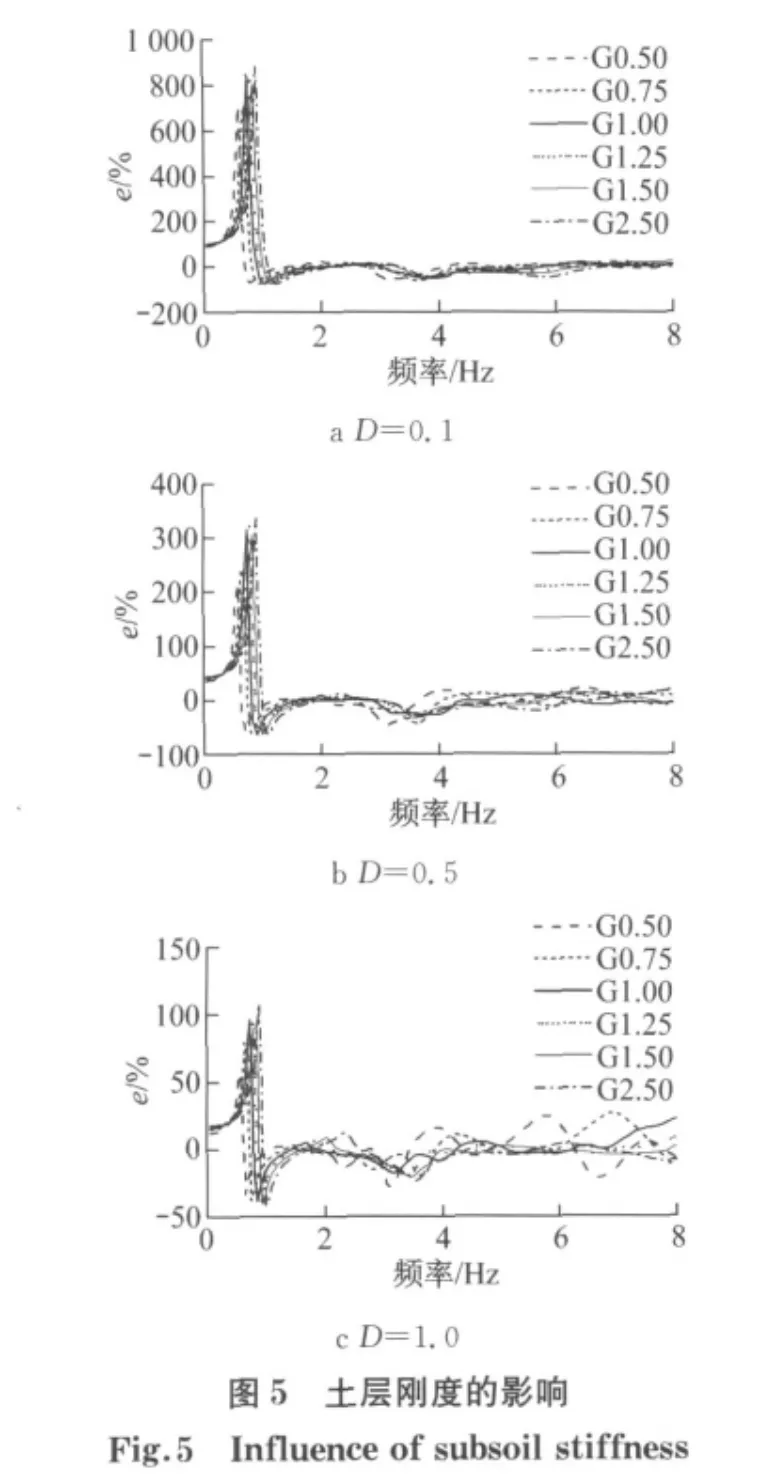
土体的软硬程度是影响SSI的关键因素之一.将各土层的剪切模量分别乘以0.50，0.75，1.00，1.25，1.50，2.00 后 进 行 分 析（分 别 记 作G0.50，G0.75，G1.00，G1.25，G1.50，G2.00）研究土体刚度的影响.图5 为0～8 Hz正弦波激振下D＝0.1，0.5，1.0 时 地 铁 车 站 顶 板 和 底 板 相 对 水 平 位 移 与D＝0时相对水平位移的相对值.由于地上结构的存在，在地上结构－土层系统的1阶频率附近相对值曲线产生了1个较大的尖点.随着土层刚度的增加，整个体系的1阶频率提高，尖点向高频移动.同时，尖点的峰值呈增大趋势，这是由于整体刚度提高，地铁车站顶板和底板相对水平位移减小，而单独地下结构－土层系统的响应比地上结构－土层－地下结构系统的响应减小稍快.不同D值的相对值曲线形状基本一致，只是随着结构间距的增加SSSI效应减小，尖点的峰值减小.当激振频率越过系统的1阶频率后，相对值基本处于零值附近波动，即SSSI效应基本为零.

图6分别为0～8Hz正弦波和R1地震波激振下地铁车站顶板和底板相对水平位移的相对值.显然，随着土层阻尼比ξ的增加相对值曲线的尖点峰值减小，SSSI效应减弱.这是由于地震波在结构间反射时更多的能量消耗于土层之中.

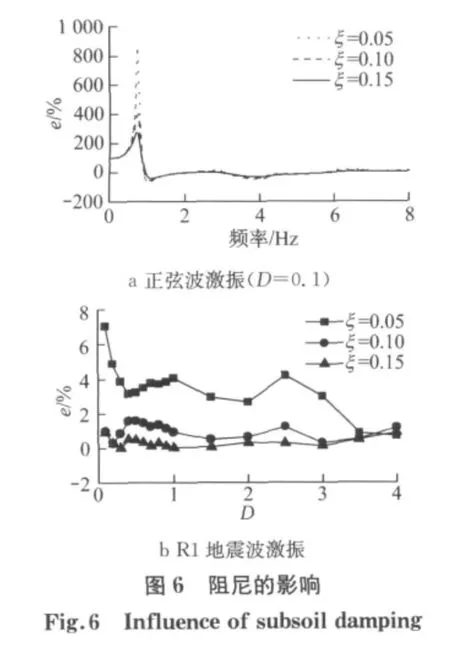
2.2 基础埋深的影响

由于基础埋深不同，土对结构的约束作用不同，土－结构系统的动力反应有所差异.图7为0～8 Hz正弦波和R1地震波激振下基础埋深H＝2.5，3.5，4.5，5.5m 时地铁车站顶板和底板相对水平位移的相对值.在正弦波激振下，随着箱基埋深的增加，相对值曲线的尖点峰值稍有增加的趋势.反应到R1地震波激振时，箱基埋深加深，相对值呈增大的趋势.这是因为基础的埋深及质量增大，与周围土体结合得更好，从而对相邻地下结构的影响就增大.

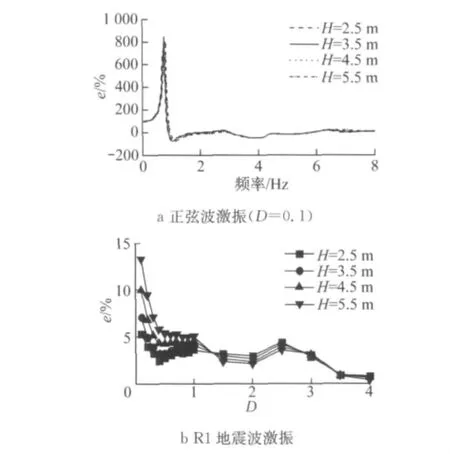
图7 基础埋深的影响Fig.7 Influence of foundation buried depth

2.3 地上结构的影响

图8a为在原有模型的基础上D＝0.1时地上结构楼层数N＝8，12，16，20的e值.显然，随着结构楼层数的增加，相对值曲线的尖点峰值增加，即在系统1阶频率附近地上结构对地下结构的影响增加.这是由于上部结构质量的增加导致了振动能量的增加，进而对地下结构的影响变大.当激振频率越过系统的1阶频率后，不论地上结构楼层数多少，相对值基本处于零值附近波动，即SSSI效应基本为零.因此，当地铁车站处于大型建筑物周围时应谨慎考虑其产生的SSSI效应.

图8b为在原有模型的基础上D＝0.1时地上结构地上部分的刚度 乘 以0.50，0.75，1.00，1.25，1.50，2.00（分别记作E0.50，E0.75，E1.00，E1.25，E1.50，E2.00）后计算的e值.相对值曲线变化不大，说明地上结构上部刚度对SSSI效应的影响几乎可以忽略.

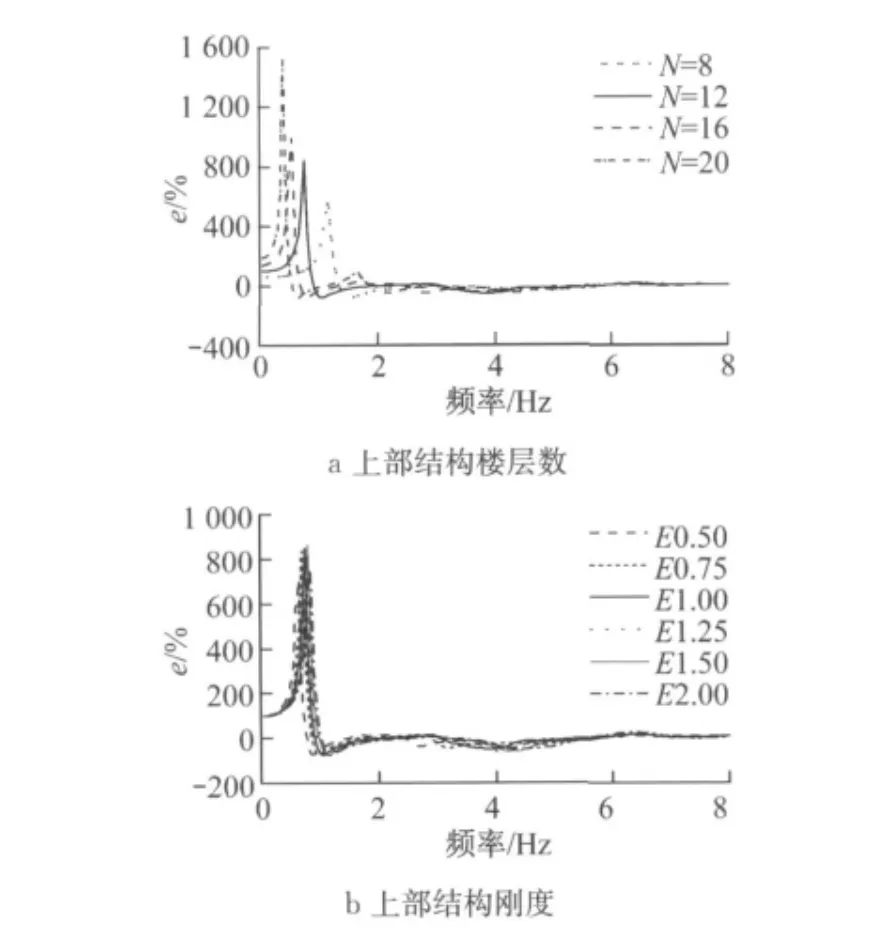
图8 上部结构的影响Fig.8 Influence of superstructure

3 结论

利用二维有限单元法分析了一系列地上结构－土层－地下结构系统的地震动力响应，初步探讨了地上结构对地下结构动力的影响.主要包括对不同地震波、结构间距、土层刚度、土层阻尼比及地上结构基础埋深、楼层数、刚度等参数的讨论.分析结果表明：地震波频谱成分的影响很大；随着结构间距增加，相互作用迅速减小；随着土层阻尼比减小、基础埋深增加、楼层数增加，相互作用增大；地上结构上部刚度对相互作用程度的影响不大.邻近地上结构的存在对地下结构地震响应的影响主要集中于地上结构的1阶频率附近.

由以上的分析结果可知，邻近地上结构的存在会严重影响地下结构的地震响应，因此，迫切需要更加深入地研究SSSI现象及其对结构地震响应的影响.

［1］ 刘晶波，李彬.地铁地下结构抗震分析及设计中的几个关键问题［J］.土木工程学报，2006，39（6）：106.LIU Jingbo，LI Bin.Issues on the seismic analysis and design of subway structures［J］.China Civil Engineering Journal，2006，39（6）：106.

［2］ 袁蕾，姜忻良.地铁换乘站不规则结构对其地震响应的影响［J］.地震工程与工程振动，2011，31（1）：74.YUAN Lei，JIANG Xinliang.Influence of irregular structure of subway transfer station on its seismic responses［J］.Journal of Earthquake Engineering and Engineering Vibration，2011，31（1）：74.

［3］ 刘晶波，刘祥庆，王宗纲，等.土－结构动力相互作用系统离心机振动台模型试验［J］.土木工程学报，2010，43（11）：114.LIU Jingbo，LIU Xiangqing，WANG Zonggang.Dynamic centrifuge model test of a soil－structure interaction system［J］.China Civil Engineering Journal，2010，43（11）：114.

［4］ Lou M，Wang H，Chen X，et al.Structure－soil－structure interaction：literature review ［J］. Soil Dynamics and Earthquake Engineering，2011，31（12）：1724.

［5］ 程磊，吕西林，李培振.考虑相邻结构影响的土－结构动力相互作用研究综述［J］.地震工程与工程振动，2010，30（2）：32.CHENG Lei，LU Xilin，LI Peizhen.A review of soilstructure dynamic interaction research considering dynamic cross interaction effect［J］.Journal of Earthquake Engineering and Engineering Vibration，2010，30（2）：32.

［6］ 刘晶波，李彬，谷音.地铁盾构隧道地震反应分析［J］.清华大学学报：自然科学版，2005，45（6）：757.LIU Jingbo，LI Bin，GU Yin.Seismic response analysis of shielded subway tunnels［J］.Journal of Tsinghua University：Science and Technology，2005，45（6）：757.

［7］ 王铁成，王卉.埋地双排复合式管体结构在SH 波作用下的动力分析［J］.地震工程与工程振动，2008，28（4）：14.WANG Tiecheng，WANG Hui.Dynamic analysis of twin underground composite pipe structures subjected to SH waves［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（4）：14.

［8］ 周德良，翁智远.弹性半空间中相邻两结构在SH 波作用下的动力响应［J］.固体力学学报，1992，13（3）：244.ZHOU Deliang，WENG Zhiyuan.The dynamic response of two parallel structures in elastic half－space under SH waves［J］.Acta Mechanica Solida Sinica，1992，13（3）：244.

［9］ 庄海洋，陈国兴.双洞单轨地铁区间隧道非线性地震反应分析［J］.地震工程与工程振动，2006，26（2）：131.ZHUANG Haiyang，CHEN Guoxing.Analysis of nonlinear earthquake response of metro double－tunnels［J］.Journal of Earthquake Engineering and Engineering Vibration，2006，26（2）：131.

［10］ 李方杰，赵凤新，张郁山，等.相对位置的地上结构对地铁地下结构地震反应的影响［J］.中国地震，2010，26（2）：201.LI Fangjie，ZHAO Fengxin，ZHANG Yushan，et al.Influence of ground building’s relative position on seismic response of subway structure［J］.Earthquake Research in China，2010，26（2）：201.

［11］ 楼梦麟，潘旦光，范立础.土层地震反应分析中侧向人工边界的影响［J］.同济大学学报：自然科学版，2003，31（7）：757.LOU Menglin，PAN Danguang，FAN Lichu.Effect of vertical artificial boundary on seismic response of soil layer［J］.Journal of Tongji University：Natural Science，2003，31（7）：757.

［12］ 楼梦麟，潘旦光.滞后阻尼在土层时域分析中的应用［J］.同济大学学报：自然科学版，2004，32（3）：281.LOU Menglin， PAN Danguang. Hysteretic damping application in time domain analysis of soil layer［J］.Journal of Tongji University：Natural Science，2004，32（3）：281.