考虑空间相关性的信控交叉口安全分析

王雪松，谢 琨，陈小鸿，王 珂

（1.同济大学 交通运输工程学院，上海201804；2.复旦大学 管理学院，上海200095）

信控交叉口是道路网络的重要节点，大量机动车、非机动车、行人在此汇集、通过和转向，是交通事故的多发点.我国由于存在大量机非混行，交叉口安全问题非常严重.无论是危险交叉口的甄别，还是提出有效的改善措施，都有赖于对信控交叉口事故发生影响因素的深入认识.考虑到信控交叉口本身的多样性（几何形态、交通特性、交通控制等），交叉口使用者的复杂性（机动车、自行车、行人），交叉口事故形态的多样性（追尾、侧碰等），信控交叉口安全分析非常复杂.

通过分析交叉口特征与事故的统计关系，可以发现影响事故发生的显著因素.不同于一般服从正态分布的数据，交通事故是小概率随机事件，事故频率具有非负性、离散性、非正态分布等特点，信控交叉口安全问题的复杂性和数据的复杂性对统计分析提出了很高的要求.传统的事故分析模型都是建立在交叉口相互独立的前提假设上的，然而在中国大城市的中心城区，交叉口间距普遍较小，交通运行相互影响.上海市区的交叉口平均间距仅为351 m.在建立交叉口事故分析模型进行安全分析时需要考虑交叉口之间的空间相关性.本文的研究目的是建立合理的针对中国大城市的信控交叉口事故统计分析模型，考虑交叉口的空间相关性，并分析影响安全的显著因素.

1 研究综述

国外围绕事故分析模型进行了大量的研究.最初采用的多元线性回归在研究事故数据时有如下缺陷：分布不合理、无法准确描述非负的事故数、无法描述事故这类小概率事件［1－3］.泊松模型是最基础的计数模型［4］，考虑了事故数据随机、离散、非负的特点，但是事故数据的过度离散性却违背了泊松模型均值等于方差的基本假设［5］.负二项模型很好地处理了事故数据过度离散的问题［6－7］，但是其基本假设是样本之间相互独立，没有考虑数据的关联性，可能造成错误的统计推断.

位于同一主干道上的信控交叉口彼此之间由于间距太小而交通流相互影响，可能诱使事故发生；相邻交叉口联合线控可减少车辆通过交叉口的停留次数，可能降低追尾事故的发生，但是不停顿的车流又有可能引起驾驶员超速行驶进而产生安全问题［8］.Poch等［6］在对Bellevue市信控交叉口进行研究时为了保证样本的独立性而特意抽取了较少量的交叉口.Abdel－Aty等最早开始考虑交叉口的空间相关性［8－9］，基于美国佛罗里达州41条主干路上476 个连续分布的信控交叉口利用广义估计方程（generalized estimating equation，GEE）建立信控交叉口事故分析模型，研究表明交叉口间距是影响交叉口总体事故和追尾事故的显著因素.GEE 适用于分析相互关联的离散数据，鲁棒性好［10］，近年来逐步用于交叉口的安全分析［8－12］.

国外的事故统计分析模型对影响信控交叉口安全的几何设计、控制属性、交通特征和区位特征进行了系统的研究.在几何设计方面，交叉口车道总数与事故总量呈现正相关性［9］，斜交交叉口由于视距问题和穿越距离增加易导致事故发生［13］，设置左转车道偏移可以降低事故的发生［14］.在交通控制方面，增加专用左转相位会降低左转事故，但是追尾事故会因为相位数增加而增加［8－9，15］.交通流量与安全的关系一直是交通分析模型研究的重点，如交叉口总流量［3，8，15］或相交道路流量［11，16］，部分研究分析了直行、左转车流与安全的关系［17－18］.在区位特征方面，2006年Abdel－Aty和Wang［8］发现商业区交叉口发生事故的几率高于居住区.2010年Guo等［17］研究发现城区的交叉口事故发生几率高于郊区.另外，考虑到不同的事故形态对应不同的原因，一些学者对追尾、侧碰、左转等事故形态进行了单独分析以鉴别影响不同事故形态的相应因素［6，9，12，14］.

在我国，由于缺乏完整可靠的事故数据，通常利用交通冲突数据进行交叉口的安全评价［19－20］.基于冲突的安全评价需要对研究区域内的交叉口进行大范围的交通冲突观测，对冲突的认定并没有统一的标准.基于事故数据的安全分析有不可替代的作用.国内应用简单回归方程、泊松模型和负二项模型对城市信控交叉口进行事故统计分析［21－22］.信控交叉口严峻的交通安全形势和迫切的改善需求对事故数据分析提出了更高的要求.

2 数据准备

①交叉口样本选择，随机选取了22条主干道上195个信控交叉口；②按照主干道和空间位置对交叉口进行分组、排序，195个交叉口分为25组；③交叉口事故、区位特征、几何设计、控制属性及交通特征数据采集，共采集了19个交叉口特征变量.

2.1 交叉口取样

利用地理信息系统（geographic information system，GIS）作为工具挑选样本，GIS作为空间数据库可直观展示主干道和信控交叉口的位置及其属性.交叉口样本的选择遵循如下原则：①所选交叉口样本都位于上海市市区，市区信控交叉口数据比较完整；②为了更好地分析交叉口间的空间关联性，选取的交叉口是沿着主干道连续的.最终挑选出22条主干道上195个十字型（或T 型）信控交叉口，分布如图1，图中数字为道路编号.

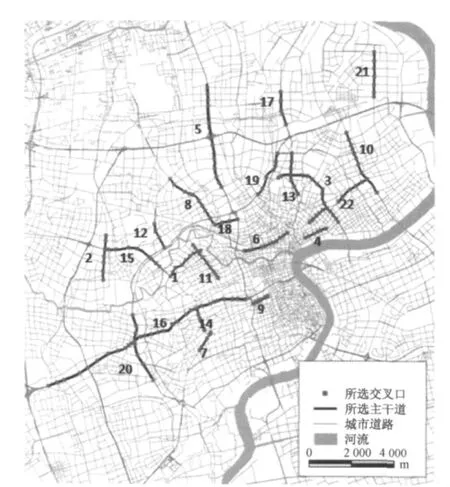
图1 主干道及信控交叉口样本分布Fig.1 Major arterials and the selected signalized intersections

2.2 交叉口分组

对于少量主干道相交处的交叉口需要根据2条主干道对交叉口的影响程度来确定该交叉口的归属.本文假定沿着交通流量大的主干道，相互间的影响更大，将此类交叉口归为交通流量较大的主干道上.

对于同一条主干道上的交叉口，如果主干道过长，导致交叉口相互影响减弱，就需要根据交叉口的空间位置对该主干道上的交叉口进行分组.两步聚类分析（twostep cluster）可以自动确定分类数，用于对交叉口进行进一步划分，输入变量为交叉口的x－y坐标.第1步形成分类特征树，同一主干道上距离最近的2个交叉口先形成1个结点，后续交叉口根据最短距离原则被分别加到现有结点上或者形成1个新的结点；第2 步使用聚类算法（clustering algorithm）对特征树的结点进行分组，并根据BIC准则（Bayesian information criterion）确定最优的分组，BIC值最小的为最优分组.结果保证同组之间交叉口相互影响最大，不同组之间影响最小.分组汇总结果如表1所示.

2.3 交叉口数据采集

交叉口区位特征包括交叉口间距、是否受高架影响；几何设计信息来自于交叉口渠化图，通过Google Earth卫星地图进行补充；信号控制信息来自 于SCATS （sydney coordinated adaptive traffic system）系统；交通特征通过线圈检测器采集的数据计算得到.交通流量由于线圈检测器部分损坏，需要对数据进行有效性检验，并对缺失的检测器流量数据进行推算，如用相邻检测器的流量数据来代替.在标定模型之前对各变量进行初步处理，如按照相位数将交叉口分为2～3相位和4～6相位2类.变量的统计性描述如表2所示.

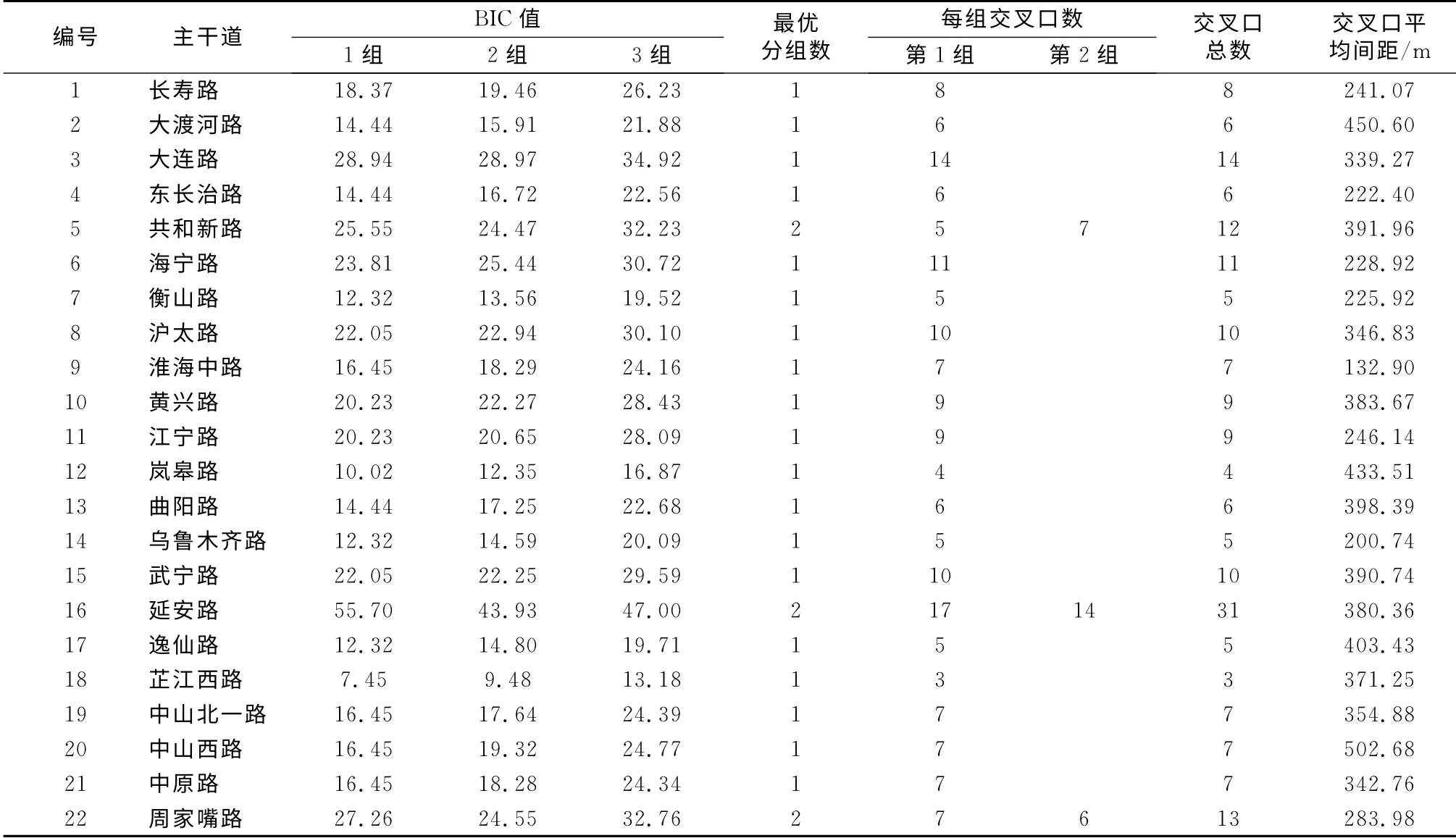
表1 信控交叉口分组汇总Tab.1 Summary of cluster analysis for signalized intersections along corridors

3 广义估计方程

3.1 模型形式

GEE 通过指定每组观测单元观测对象之间的关系矩阵形式［23］克服数据之间相关性的影响，可以用来分析相关联的多层次数据结构.GEE 假设因变量的边际期望为所有独立变量的线性函数，方差为均值的已知函数.

根据交叉口所属的主干道及交叉口的空间位置关系将交叉口分为K组（K＝25），每组ni个交叉口（ni≤17）.假设属于同一组的交叉口相互影响，不同组的交叉口相互独立.第i组交叉口的事故数为Yi＝（yi1，…，yini）′，对 应 的 期 望 值 为E（Y）＝μi＝（μi1，…，μini）′，其中yini为第i组第ni个交叉口的事故数；μini为该交叉口事故期望值.Xij＝（xij1，…，xijp）′是交叉口事故yini的p×1的解释变量矩阵，其中p为解释变量的个数.因变量yini边际期望μini是解释变量Xij的线性组合的已知函数，即g（μini）＝X′ijβ，其中g为连接函数；β为解释变量的参数.考虑到事故离散性的特点，以负二项分布为连接函数，对β进行参数估计的方法如下为P×ni阶矩阵的偏导数，

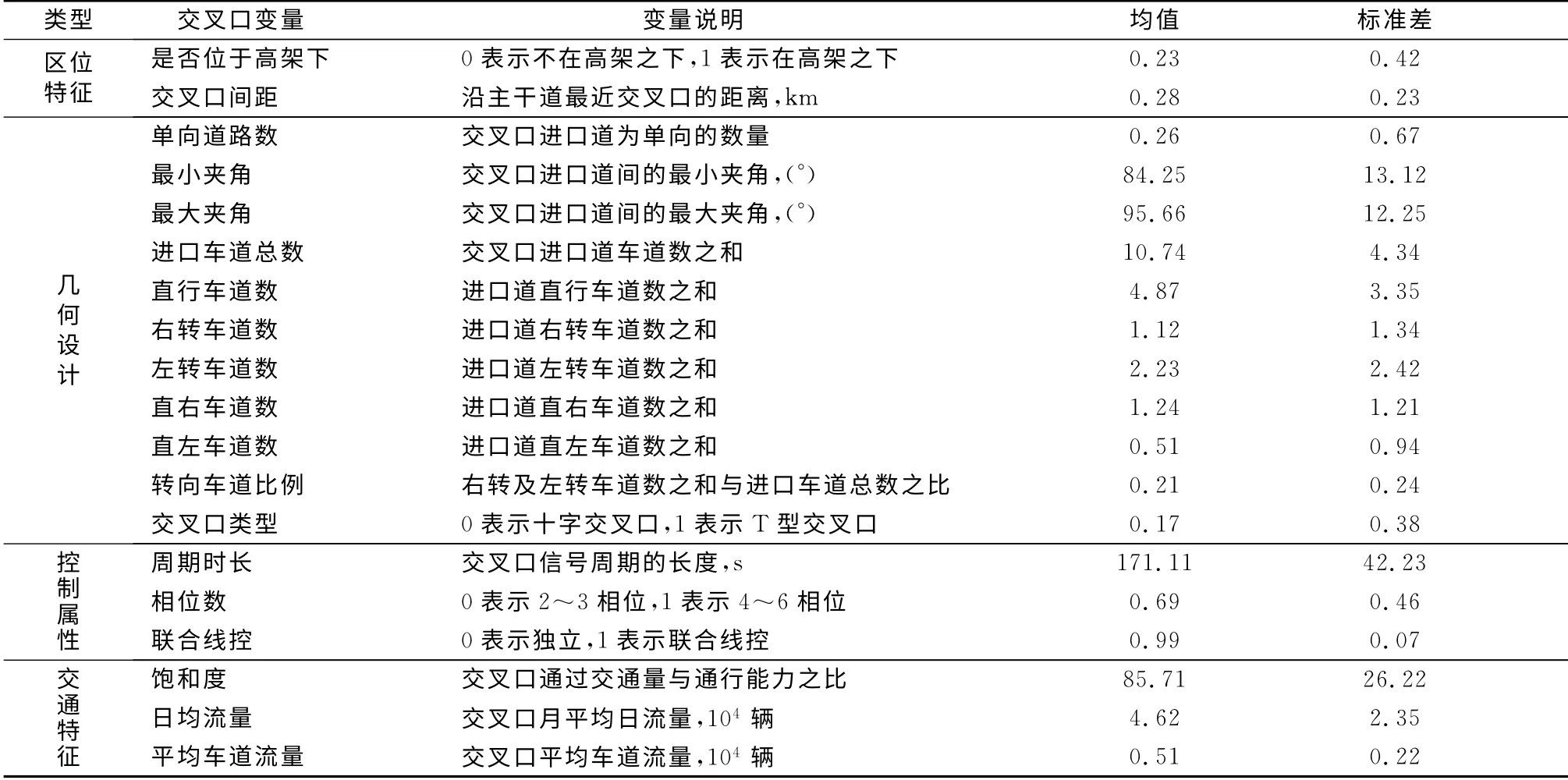
表2 变量的统计性描述Tab.2 Descriptive statistics for variables

Vi是Yi的协方差，协方差的估计方法为，式中：φ为离散系数；Ai是一个ni×ni的对角线矩阵，对角线上的元素为V（μini），一般来说，可以认为所有的交叉口都有相同的Vi形式；Ri（α）是一个ni×ni的空间关联矩阵，它可以反映交叉口的空间关联结构，α是其参数，α的大小表征交叉口相互之间空间关联的强弱.以下是几种常用的关联矩阵形式［10］.

（1）独立型关联矩阵（independent）.假设同组内交叉口之间是相互独立的.这种情况下GEE 估计的结果与一般广义线形方程（GLM）结果一致，但两者的标准差不同，式中：yij，yik分别为第i组第j，k个交叉口的事故数.

（2）等相关型关联矩阵（exchangeable）.假设同组内交叉口两两之间相关性相等.Corr（yij，yik）＝式 中：α的 估 计 值α＾＝为皮尔逊残差（Pearson residuals）.离散参数φ通过来估计.

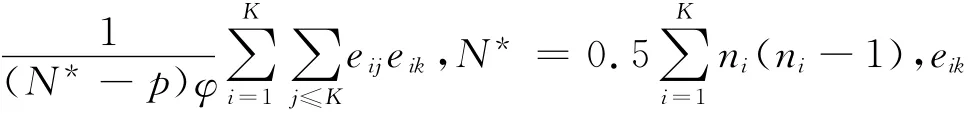
（3）自回归型关联矩阵（autoregressive）.假设同组交叉口之间的相关性由它们的间距决定.随着交叉口间间隔的增加，关联度降低.Corr（yij，yik）＝为α的估计值，其中t为交叉口的间隔，若交叉口按照顺序沿着干道依次编号，则t为交叉口编号之差

3.2 模型检验

GEE没有真实的似然函数，而是利用拟似然函数的方法进行参数估计，QIC（quasi likelihood under independence model criterion）可以来判别关联矩阵形式是否能够反映数据的结构特征［24］.QIC 值越小，模型越优.另外，还可以用累计残差绝对值（sum of absolute errors，SAE）评价模型拟合优度，其值越小，模型越优［25］.累计残差绝对值计算公式如下：，式中：yi为事故实际发生数；f（x1i，x2i，…，xmi）为按照模型估计的事故数；n为样本总数；m为模型中解释变量的数目.

Type III检验可以用来比较解释变量的显著性.通过Type III检验可得到每个解释变量的Chisquare值和p值.其中，Chi－square值指基于所有变量建立的模型的广义统计值与除去该解释变量后的广义统计值之差.p值的大小表明该解释变量在模型中还包含其他变量时对因变量解释的显著程度.p值越小，变量在模型中的相对作用越显著［8］.

4 模型估计结果

基于22条主干道195 个信控交叉口的事故数据和交通特征数据，利用GEE 建立事故模型.考虑到交叉口间不同的空间关系，GEE 分别以独立型、等相关型、自回归型矩阵作为关联矩阵.标定传统的负二项模型作为对照.模型标定和检验结果如表3.

模型的离散系数（dispersion）均显著大于零，这表明事故数据具有明显的过度离散特征.传统的负二项模型的累计残差绝对值为5 029.166，大于GEE的，表明GEE 拟合结果优于负二项模型，考虑交叉口空间关联可以提高模型的拟合度，比较关联矩阵不同的GEE，QIC值和SAE值均以自回归型矩阵为最优，这说明自回归型矩阵形式与交叉口空间关联的特征最为相符.GEE 自回归型同组交叉口之间的关联系数如表4所示，在同一分组内，交叉口间的空间相关性由它们的间距决定，随着交叉口间隔的增加，彼此的关联系数降低.独立型同组交叉口之间的关联系数均为零，等相关型同组交叉口之间关联系数为定值0.42.

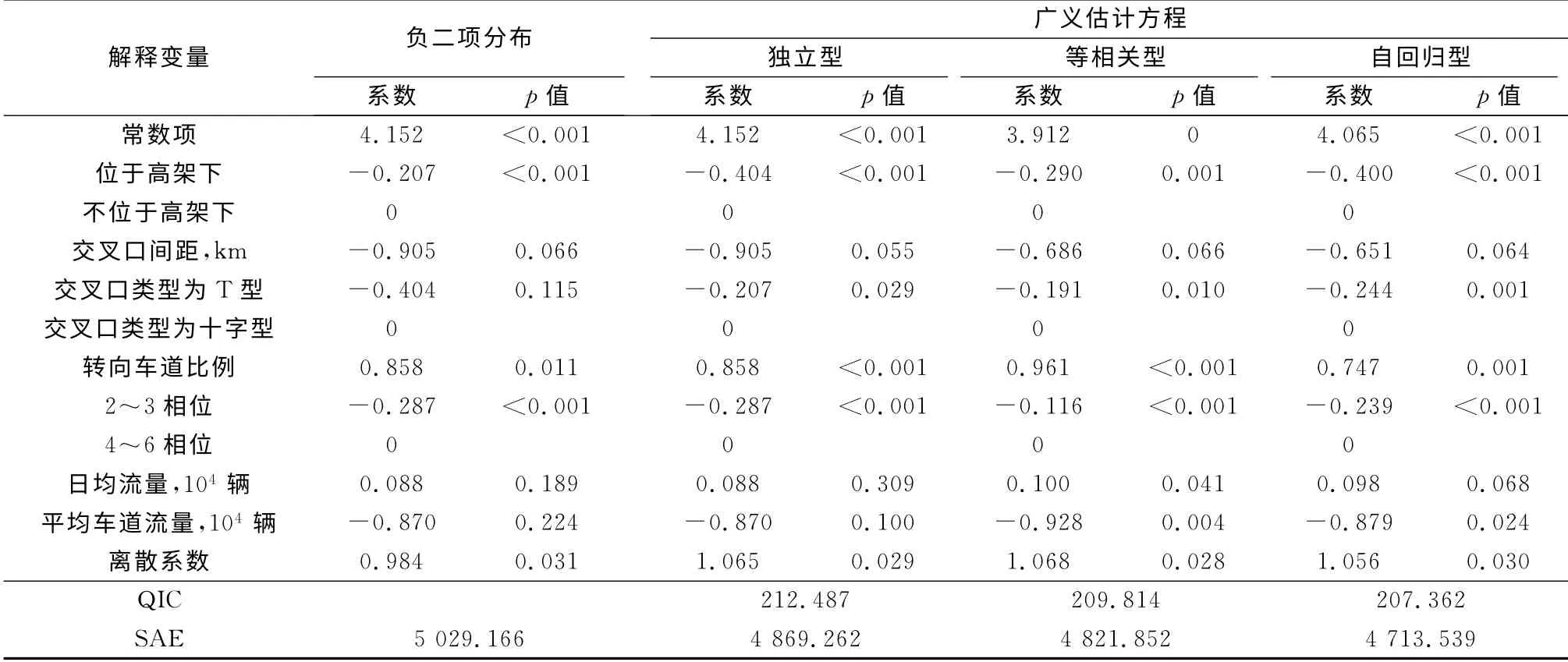
表3 事故分析模型估计结果Tab.3 The estimation results of crash frequency models

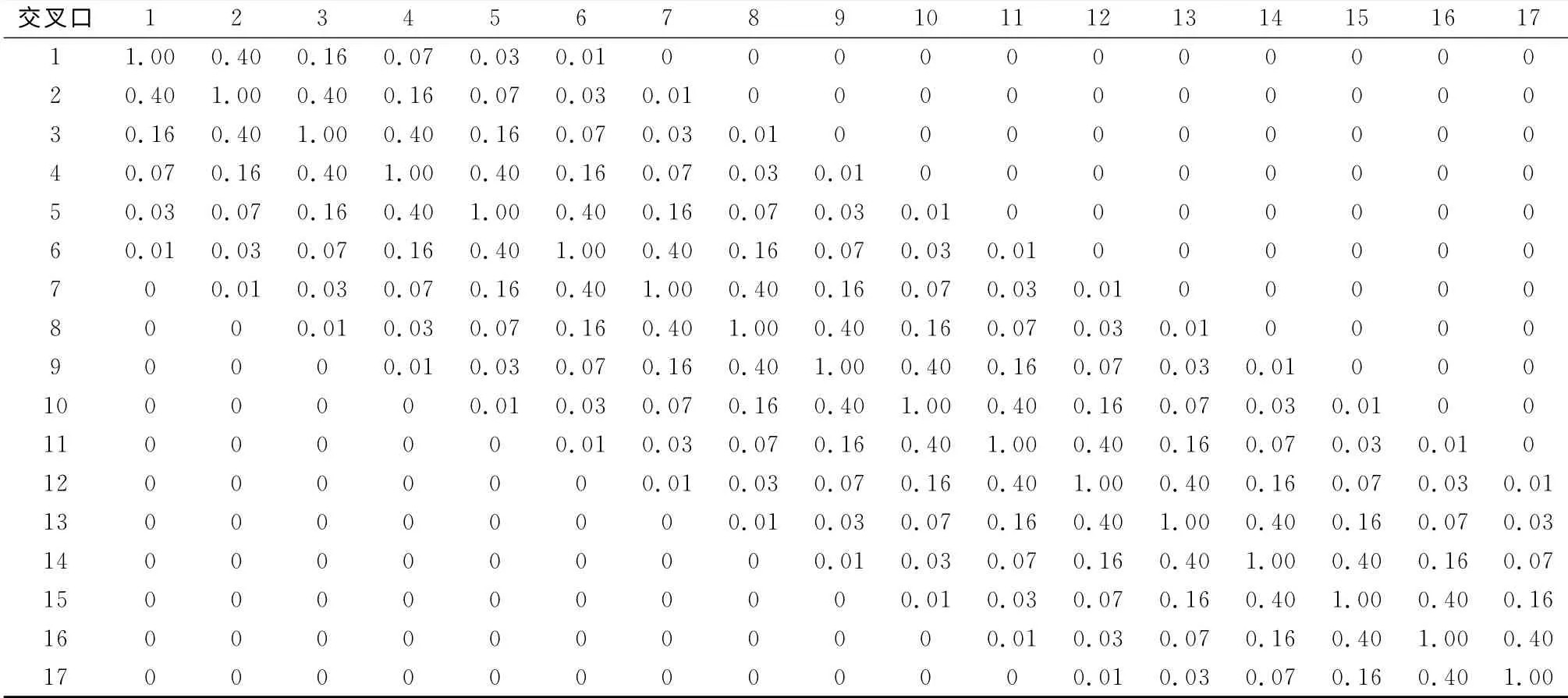
表4 估计的自回归型关联矩阵Tab.4 The estimated working correlation structure of autoregression

5 安全影响因素分析

对比传统的负二项模型和GEE 的估计结果，交叉口类型、日均流量、平均车道流量3个变量在负二项模型中不显著，在GEE 中显著.考虑到GEE 拟合数据较优，所以安全显著因素分析基于以自回归型为方差矩阵的广义回归方程.显著变量从交叉口区位特征、几何设计、控制属性、交通特征中分析出7个影响交叉口安全的因素：是否位于高架下、交叉口间距、交叉口类型、转向车道比例、相位属性、日均流量、平均车道流量.利用Type III检验进一步比较事故分析模型中解释变量的显著性，检验结果如表5所示.根据表中自回归型对应的GEE 变量的p值，可以得出安全影响因素相对重要度排序：日均流量、平均车道流量、交叉口类型、是否位于高架下、相位属性、转向车道比例、交叉口间距.

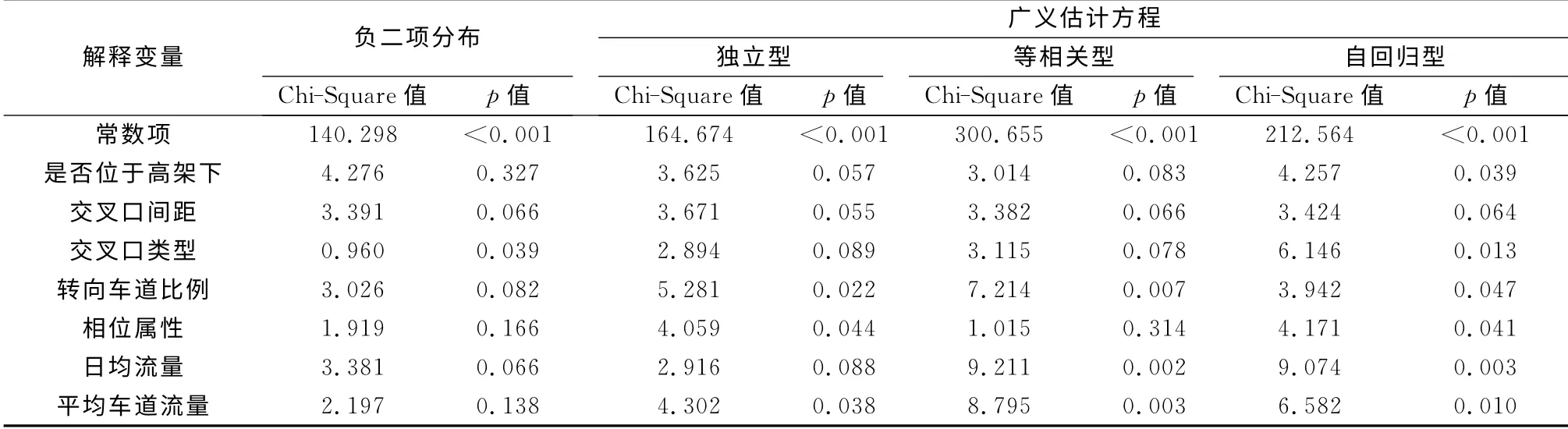
表5 Type III检验结果Tab.5 Results of type III analysis

结合表3模型估计结果和表5Type III检验结果分别对信控交叉口区位特征、几何设计、控制属性、交通特征中各影响因素解释如下：

（1）区位特征.位于高架下的交叉口发生事故的可能性较大.由于高架的存在，交叉口视距会受到影响；高架和地面道路之间常设有上下高架的匝道，位于高架下的交叉口容易受到上下匝道车流的干扰.交叉口间距回归系数为负数，表明临近交叉口距离越小发生事故的可能性越大.Abdel－Aty和Wang对佛罗里达州交叉口事故数据分析也得出了相同的结论［8－9］.进一步验证了同一主干道上相邻交叉口之间存在影响的假设.交叉口间距过小，运行相互影响，车辆可能频繁变道，会造成交通混乱，增加事故发生几率.

（2）几何设计.交叉口类型在模型中的相对作用比较显著.T 型交叉口回归系数为－0.244，表明T 型交叉口比十字交叉口发生事故的概率约小24%.与T 型交叉口相比，十字交叉口交通组织更为复杂，冲突点更多，发生事故可能性更大.转向车道比例对发生交通事故有显著的正效应（显著性水平为0.022），左转车辆越多，发生左转与对向碰撞的几率越大；右转车辆越多，与行人、非机动车冲突的几率越大；同时转向车流也增加了合流碰撞的几率.

（3）控制属性.相位数多的交叉口更容易发生事故，这也被其他研究证实［6，9］.虽然更多的相位可以将交通流在时间上进行分离，但是这也会增加追尾事故发生的可能［26］.另外，闯红灯等违章行为往往是在信号切换时产生，因此信号相位频繁切换会增加事故发生的机率.

（4）交通特征.交通流量是影响安全最显著因素［6，8－9］.根据Type III检验结果，交叉口日均流量在模型中的相对作用最为显著.日均流量与事故数成正相关（回归系数为0.098），流量越大的交叉口发生碰撞的可能性越大，在其他条件保持不变的前提下，日均流量每增加10 000辆，事故总数会增加10%左右.平均车道流量反映了通过交叉口的交通流密度，国外研究认为平均车道流量越大，则车辆间距越小，从而会导致更多的事故［7－8］.本研究发现平均车道流量与事故数成负相关（回归系数为－0.879）.国内外交通环境和驾驶员驾驶特征不同，在国内车流密度比较大的交叉口交通控制设施良好（如闯红灯摄像头），车辆违章概率小.

6 结语

利用广义估计方程建立了交叉口事故分析模型，分析了主干道信控交叉口之间的空间关联性，交叉口安全影响因素从大到小排序为：日均流量、平均车道流量、交叉口类型、是否位于高架下、相位属性、转向车道比例、交叉口间距.交叉口间距越小、转向车道比例越大、相位数越多、日均流量越大、平均车道流量越小，事故产生的风险越大；十字交叉口、位于高架下的交叉口的事故发生几率分别比T 型交叉口、不位于高架下的交叉口高.本文研究成果可以为交通规划、设计、管理提供依据，在交通规划设计层面，考虑到交叉口间距对安全的影响，尽量避免交叉口间距过小；在交通管理层面，需要重点关注流量大、多相位、在高架下的交叉口，这些交叉口往往是事故的多发点.

［1］ Miaou S P，Lum H.Modeling vehicle accidents and highway geometric design relationships ［J］.Accident Analysis ＆Prevention，1993，25（6）：689.

［2］ Jovanis P，Chang H.Modeling the relationship of accidents to miles traveled［J］.Transportation Research Record，1986，1068：42.

［3］ Chin H C，Quddus M A.Applying the random effect negative binomial model to examine traffic accident occurrence at signalized intersections［J］.Accident Analysis ＆Prevention，2003，35（2）：253.

［4］ Cameron A C，Trivedi P K.Regression analysis of count data［M］.London：Cambridge University Press，1998.

［5］ Maher M J，Summersgill I.A comprehensive methodology for the fitting of predictive accident models ［J］.Accident Analysis ＆Prevention，2006，28（3）：281.

［6］ Poch M， Mannering F. Negative binomial analysis of intersection－accident frequencies ［J ］. Journal of Transportation Engineering，1996，122（2）：105.

［7］ Abdel－Aty M，Radwan A E. Modeling traffic accident occurrence and involvement ［J］. Accident Analysis ＆Prevention，32（5）：633.

［8］ Abdel－Aty M， Wang X.Crash estimation at signalized intersections along corridors：analyzing spatial effect and identifying significant factors［J］.Transportation Research Record，2006，1953：98.

［9］ Wang X，Abdel－Aty M.Temporal and spatial analyses of rear－end crashes at signalized intersections ［J］.Accident Analysis ＆Prevention，2006，38（6）：1137.

［10］ Liang K Y，Zeger S L.Longitudinal data analysis using generalized linear models［J］.Biometrika，1986，73（1）：13.

［11］ Lord D，Persaud B.Accident prediction models with and without trend：application of the Generalized Estimating Equations（GEE）procedure ［J］.Transportation Research Record，2000，1717：102.

［12］ Wang X，Abdel－Aty M.Modeling left－turn crash occurrence at signalized intersections by conflicting pattern［J］.Accident Analysis ＆Prevention，2008，40（1）：76.

［13］ Hall R.Accidents at four－arm single carriageway urban traffic signals ［M］.Berkshire：Transport Research Laboratory，1986.

［14］ Wang X，Abdel－Aty M.Right－angle crash occurrence at signalized intersections［J］.Transportation Research Record，2007，2019：156.

［15］ Wang X，Abdel－Aty M，Brady P.Crash estimation at signalized intersections：significant factors and temporal effect［J］.Transportation Research Record，2006，1953：10.

［16］ Mountain L，Maher M，Fawaz B.The influence of trend on estimates of accidents at junctions［J］.Accident Analysis ＆Prevention，1998，30（1）：641.

［17］ Guo F， Wang X， Abdel－Aty M. Modeling signalized intersection safety with corridor－level spatial correlations［J］.Accident Analysis ＆Prevention，2010，42（1）：84.

［18］ Hauer E，Lovell J.Estimation of safety at signalized intersections ［J］.Transportation Research Record，1988，1185：48.

［19］ 成卫，丁同强，李江.道路交叉口交通冲突灰色评价研究［J］.公路交通科技，2004，21（6）：97.CHENG Wei，DING Tongqian，LI Jiang.Evaluation of traffic conflict based on gray theory at intersection［J］.Journal of Highway and Transportation Research and Development，2004，21（6）：97.

［20］ 项乔君，卢川，吴群，等.基于冲突严重性划分的公路平交口安全评价［J］.公路交通科技，2008，25（8）：128.XIANG Qiaojun，LU Chuan，WU Qun，et al.Traffic safety evaluation on highway intersection based on severity division of traffic conflict［J］.Journal of Highway and Transportation Research and Development，2008，25（8）：128.

［21］ 裴玉龙，马艳丽.寒冷地区城市道路交叉口条件与交通事故关系［J］.哈尔滨工业大学学报，2005，37（1）：130.PEI Yulong，MA Yanli.The relationship between condition and traffic accidents of urban road intersections in the cold region［J］.Journal of Harbin Institute of Technology，2005，37（1）：130.

［22］ 张勇，王相平，姜楠.三路无信号交叉口事故预测模型分析［J］.兰州交通大学学报，2007，26（6）：72.ZHANG Yong，WANG Xiangping，JIANG Nan.Research on the crash prediction model of three－phase unsignalized intersection［J］.Journal of Lanzhou Jiaotong University，2007，26（6）：72.

［23］ McCullagh P，Nelder J A.Generalized linear models［M］.London：Chapman and Hall，1989.

［24］ Pan W. Akaike＇s information criterion in generalized estimating equations［J］.Biometrics，2001，50（1）：120.

［25］ Wooldbridge J. Introductory econometrics： a modern approach［M］.Boston：South－Western College Publishing，2002.

［26］ Roess G P，Prassas E S，McShane W R.Traffic engineering［M］.3rd ed.Upper Saddle River：Pearson Prentice Hall，2004.