稳定夹送辊理论设计方法

孙亚波，张康武，岳国富，丁开荣，刘云飞，邓良丰

(中国重型机械研究院股份公司，陕西 西安 710032)

0 前言

为了保证带钢稳定运行，精整机组通常需要设置若干稳定辊稳定带材，还设有张力夹送辊夹送带材，使得机组设备庞大，长度增加，不利于稳定运行。为了克服此缺点，中国重型机械研究院股份公司将稳定辊和张力夹送辊的功能合一，开发了稳定夹送辊，缩短了机组长度，运行更加稳定，且减少了投资。稳定夹送辊由一根传动辊和3根空转辊组成，都为包胶辊，如图1所示。上夹送辊为传动辊且可升降，用于夹送带钢，不参加机组联动，其余为空转辊。夹送辊与稳定辊距离、稳定辊与转向辊距离都为a，mm;稳定辊下辊面与下夹送辊 (或转向辊)上辊面高度差为b，mm;Z为带钢与竖直线夹角，rad。

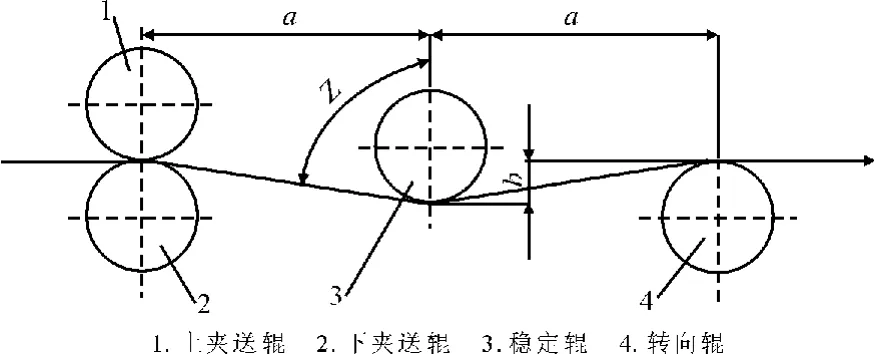
图1 稳定夹送辊结构图Fig.1 Structure of stabilizing pinch roll

在设计稳定夹送辊时，主要未知参数有:减速电机功率P、辊径D、距离a、距离b。以往稳定夹送辊设计主要依靠现场经验，参照原有结构，缺乏理论计算，精度不高，容易导致带钢出现塑性变形或者擦划伤。本文提出了一种稳定夹送辊理论设计方法，通过模型耦合迭代进行结构设计，更加准确、可靠。

稳定夹送辊设计原则:在稳定夹送辊上运行的带钢不得发生塑性变形;在机组加减速时，空转辊与带钢之间不得发生打滑而划伤带钢。涉及的计算模型:(1)夹送力计算模型。按照带钢悬垂度理论计算稳定夹送辊夹送力，进而计算电机功率。(2)带钢临界塑性变形模型。计算带钢达到临界塑性变形状态时的最大挠度，即距离b的最大值。(3)空转辊打滑模型。在机组加减速时，判断空转辊是否会发生打滑。

1 夹送力计算模型

稳定夹送辊的传动辊仅用于带钢穿带，不参与机组联动。因此，传动电机功率取决于夹送力与机组穿带速度。夹送力T的取值应该保证带钢悬垂度在一定范围之内，按式 (1)计算［1］:

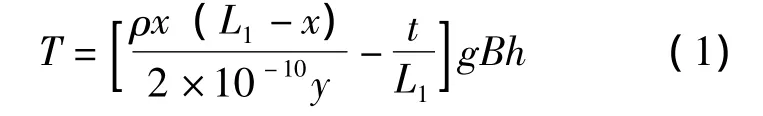
式中，y为距1#辊x处带钢悬垂量/cm;x为距1#辊距离，cm;ρ为带钢密度，kg/m3;L1为1#辊与2#辊中心距，cm;t为1#辊与2#辊辊面高差，cm;B、h为带钢宽度、厚度，cm;T为夹送力，N;g为重力加速度，9.8 m/s2。

传动电机功率P按式 (2)计算:

式中，v为穿带速度，m/min;P为功率，kW。

计算结果能够保证稳定夹送辊具有足够的夹送力，满足带钢顺利穿带的要求。

2 带钢临界塑性变形模型

带钢在稳定夹送辊上运行时，不允许产生塑性变形。以往的做法是按照式 (3)计算辊径D，认为当辊径大于等于计算值，带钢就不会发生塑性变形［2］。

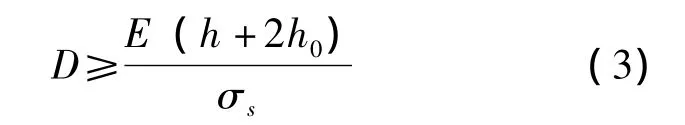
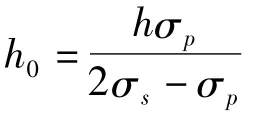
本文经过深入研究后认为，即使辊径D小于式 (3)计算值，只要稳定辊下辊面与下夹送辊 (或转向辊)上辊面高度差b小于某一值，带钢也不会发生塑性变形。根据此观点，推导出求解b值的带钢临界塑性变形模型。

将下夹送辊与转向辊之间的带钢简化为如下模型:简支矩形板模型，两对边简支，另两边自由，宽度为B，长度为2a，中间受集中力作用。假定带钢到达临界塑性变形状态，则带钢力矩为塑性弯曲力矩MW。此时，带钢的最大挠度可认为是b的最大值，由式 (4)确定:

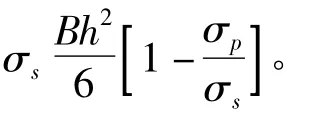
只要b满足式 (4)，即使辊径 D小于式(3)计算值，带钢也不会发生塑性变形。但是，辊径D要满足空转辊的刚度、强度要求，即辊径要大于等于最小辊径D0。

3 空转辊打滑模型

为了防止带钢擦划伤，在机组加减速时空转辊与带钢之间不允许发生打滑现象。空转辊不打滑条件为，空转辊与带钢之间的摩擦力矩大于等于空转辊的惯性力矩。

为了保证空转辊与带钢之间不发生打滑，可以从两方面考虑:一是尽量减小空转辊的惯性力矩，即尽量减小辊径D。二是空转辊与带钢之间必须有足够大的包角，保证空转辊和带钢之间形成足够大的摩擦力矩。

3.1 空转辊转动惯量计算

空转辊转动惯量J按式 (5)计算［3］:

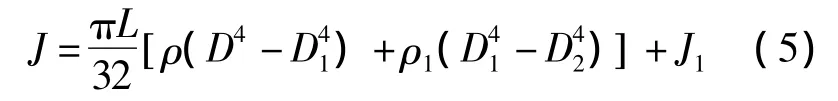
式中，L为辊身长度，m;D、D1、D2为分别为包胶层外径、钢辊外径、钢辊内径，m;ρ1为包胶层密度，kg/m3;J1为轴的转动惯量，kg.m2。

3.2 空转辊角减速度计算

机组快停时的减速度绝对值大于正常加减速时的绝对值，而急停一般不做带钢擦划伤保证。所以，要计算快停减速度绝对值。空转辊角减速度ε(rad/s2)按式 (6)计算:

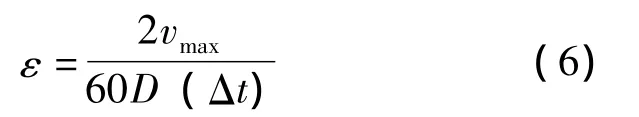
式中，vmax为机组最高工作速度，m/min;Δt机组要求的快停时间，s。

3.3 空转辊惯性力矩计算

空转辊的惯性力矩Mg(N·m)按式 (7)计算:

3.4 空转辊和带钢之间的摩擦力矩计算

空转辊和带钢之间的摩擦力矩Mf(N·m)按式 (8)计算:

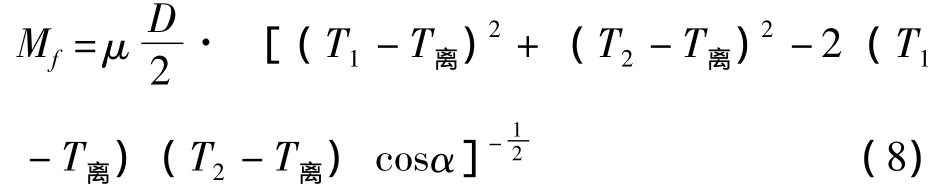
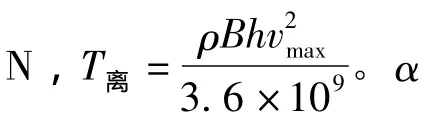
对于稳定夹送辊，包角α大小还受稳定辊下辊面与下夹送辊 (或转向辊)上辊面高度差b的制约。下夹送辊包角为α=π/2－Z;稳定辊包角为α=π－2Z;转向辊包角为α=π/2－Z;夹角Z按式 (9)迭代计算。

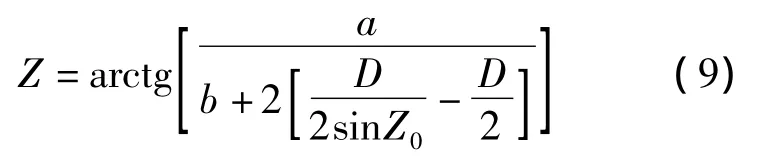
具体求解步骤如下:

(2)代入式 (9)求解得到新的结果Z*;

(3)令Z0=Z*，代入式 (9)求解得到新的结果Z*;

(5)得到夹角Z=Z*。

进而，得到包角α。

3.5 空转辊不打滑条件

空转辊不打滑的条件为:空转辊和带钢之间的摩擦力矩大于等于空转辊的惯性力矩，即:

式中，A为安全系数。

空转辊打滑模型可以通过理论计算判断空转辊与带钢之间是否会发生打滑现象，以此为据，来进行稳定夹送辊结构设计。

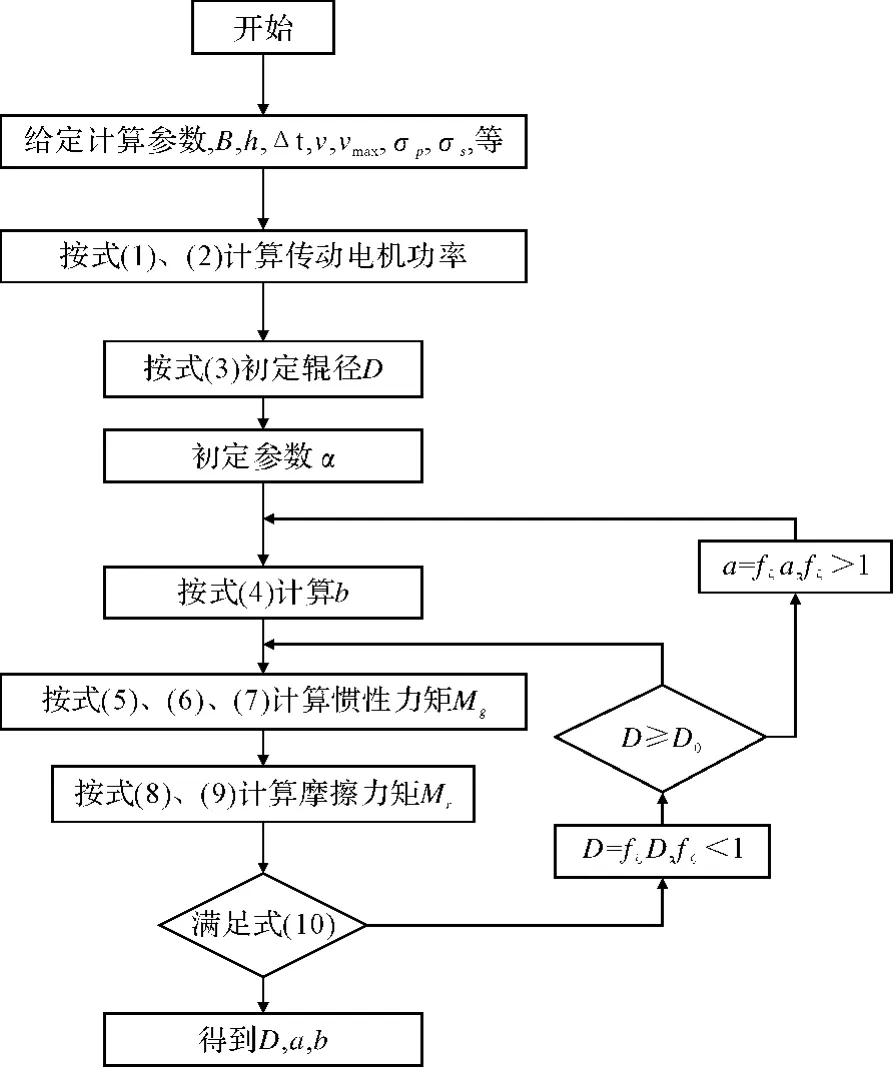
图2 稳定夹送辊设计流程图Fig.2 Flow chart of stabilizing pinch roll design

4 稳定夹送辊理论设计方法

稳定夹送辊设计计算方法和步骤如下:

(1)给定计算参数，给定满足强度、刚度要求的最小辊径D0;

(2)按照夹送力计算模型计算传动电机功率;

(3)按照式 (3)初定辊径D;

(4)初定距离a;

(5)按照带钢临界塑性变形模型计算距离b;

(6)按照空转辊打滑模型判断空转辊与带钢之间是否会发生打滑，如果不打滑，则输出计算结果，设计结束;如果发生打滑，令D=fεD，并判断D是否等于大于D0，如果等于大于D0，按步骤 (6)重新计算并判断是否发生打滑，如果小于D0，令，转到步骤 (5)计算。

计算流程图如图2所示，通过耦合迭代计算，得到稳定夹送辊传动电机功率P，辊径D，结构参数a、b。

5 算例

按照图2所示的计算流程图，编制了计算程序，以某精整机组为例，进行了稳定夹送辊的结构设计计算。某精整机组的带宽B=1 300 mm，带厚h=0.55 mm，张应力σp=30 MPa，屈服强度σs=275 MPa，最高工作速度vmax=1 000 m/min，快停时间为Δt=23 s。分析下夹送辊的受力，得出满足刚度、强度要求的最小辊径为100 mm。代入程序计算得到:减速电机功率P=2.2 kW，D=160 mm，a=420 mm，b=60 mm。这样便得到了稳定夹送辊的主要结构参数。

6 结论

(1)本文建立了夹送力计算模型、带钢临界塑性变形模型、空转辊打滑模型，将三个模型耦合迭代，提出了稳定夹送辊的理论设计方法，并编制了计算程序，改变了以往过多依靠经验的弊端，合理、准确地设计稳定夹送辊的结构。

(2)本文提出的稳定夹送辊理论设计方法，即可保证带钢不产生塑性变形，又可消除带材表面擦划伤现象的发生，提高了产品质量。

［1］严兴华.彩色涂层钢板生产线的带钢悬垂度控制［D］.广州:广东工业大学，2007.

［2］连家创.矫直理论与卷取原理 ［M］.北京，机械工业出版社，2011.

［3］张勇安，景群平，万保平，等.一种新型开头夹送辊的动力学分析及控制方法 ［J］.重型机械，2005(4):9－12.