一种新的非线性非高斯信号分离方法

王忠勇，李 响，王行业，段琳琳，2

(1.郑州大学信息工程学院，河南郑州450001;2.解放军信息工程大学 理学院，河南郑州450001)

0 引言

随着非线性科学的发展，信号分离成为当今信息处理领域的热门课题［1-2］.在信号分离中，需要根据系统观测数据以及先验估计信息，通过一定算法计算出所需估计量.当系统参数未知时，还需同时估计系统的状态和参数，从而实现多路信号的分离.经典的扩展卡尔曼滤波算法是解决此类问题的常用方法［3］，但在处理非线性非高斯对象时，该方法就会出现较大偏差.

粒子滤波(Particle Filtering:PF)［4］是一种蒙特卡洛(Monte Carlo)方法，在处理非线性非高斯系统中参数估计和状态滤波问题上具有不可替代的优势［5-7］，近年来受到广泛的关注.研究参数未知信号分离问题，可以把混合信号和系统参数看成一组高维状态，根据贝叶斯理论，该状态的联合后验密度概率函数包含该状态所有信息.笔者在PF算法基础上采用标准贝塔分布的核平滑收缩技术避免非时变参数粒子退化.仿真结果表明，本文算法能有效实现非线性非高斯信号的分离.

1 问题的提出

由于接收信号不仅包含所需信号和加性噪声，而且还包括其他有用信号，这就需要去除加性噪声同时恢复各路有用信号.

目前大量信号分离算法的研究对象是基于线性系统、高斯假设的［1-2］，然而在实际中，信号的混合方式不再是简单的线性高斯混合，于是研究非线性非高斯系统的信号分离更具有应用价值.EKF(扩展卡尔曼滤波)和UKF(无味卡尔曼滤波)方法［3］把非线性问题线性化，在高斯噪声情况下，可以获得较好的信号分离性能，然而对于非高斯噪声，该方法性能会严重恶化.刘凯等［8］利用PF算法对含非高斯噪声的线性系统进行信号分离，但非线性系统在实际中有更广泛的应用.笔者拟采用PF方法和核平滑收缩技术研究非线性系统的信号分离问题，提高粒子采样率，使信号精确分离.

假设接收信号yk由L个混合信号x=1}组成.在参数未知时，含有过程噪声和观测噪声vk的信号分离动态系统的状态空间模型可以描述为

式中:fi(·)表示第i个动力学方程表示第i路信号在k时刻的状态;为系统未知参数(这里考虑的参数为非时变参数，即为混合向量;h(·)是一个可微分的非线性函数;vk是均值为0，方差为σ2的背景噪声.

研究的问题可归结为:在上述状态空间模型下，由接收到的信号序列 y1:k={y1，y2，…，yk}递推估计联合状态

2 基于粒子滤波的盲分离算法

对于未知参数的信号分离问题，欲分离多路信号则必须先估计出未知参数.笔者用核平滑收缩技术产生参数估计粒子，再利用PF方法对参数估计粒子对应的信号状态抽样产生状态粒子集，最终完成多路信号的参数和状态分离.

2.1 粒子滤波原理

PF适用于任何能用状态空间模型描述的系统.该算法核心思想是利用从状态后验分布p(z1:k|y1:k)中抽取的离散样本点来近似状态后验分布，把积分运算转化为求和运算.通常很难直接从p(z1:k|y1:k)中抽样产生粒子，因此需引入一个便于抽样的已知分布，即重要性函数q(z1:k|y1:k).定义重要性权重为

联合后验密度概率可近似估计为

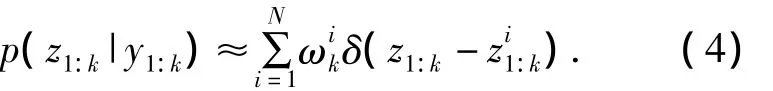
假设重要性函数可以分解为

此时重要性权重可表示为

当选取状态转移函数p(zk|zk-1)为重要性函数时，由式(3)～(6)重要性权重可化简为

在参数未知的情况下，需要利用p(zk|zk-1)同时实现参数粒子和状态粒子的更新，即

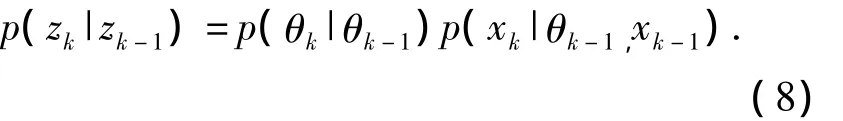
2.2 参数核平滑收缩技术

由于粒子滤波进行非时变参数估计时会出现无法增加参数粒子多样性的问题，导致参数粒子退化，从而影响参数估计的精度，于是如何避免信息丢失是解决参数粒子退化的关键问题.

对于非时变参数估计，亟须解决参数后验分布 p(θk|θk-1，y0:k)的近似问题.West提出基于自适应重要性抽样的核平滑方法［9］:假设在k-1时刻，参数粒子及重要性权重分别，则当前时刻参数后验分布可用核平滑概率近似:

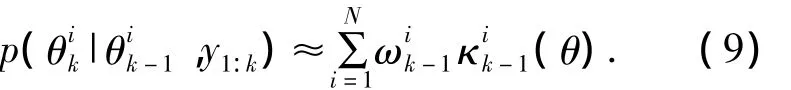
此时 p(θk|θk-1，y0:k)的均值、方差与 k-1 时刻保持一致，从而避免参数粒子退化，保证信息完整性.

2.3 基于粒子滤波的信号分离

通过上面的阐述可以看出:研究参数未知情况的信号分离问题，需在核平滑收缩技术保证参数粒子信息完整性的同时采用核分布为贝塔分布的核函数，从而提高参数粒子的采样效率和估计的准确性.在此基础上可抽样产生状态估计所需要的状态粒子集，最终完成多路信号的分离.

设k=1，…，M，针对式(1)和(2)的非线性系统，给出未知参数的信号分离算法，步骤如下:

步骤1 初始化:由初始分布p(x0，θ0)抽样得到

步骤2 参数和状态更新:由式(10)、(11)得到k-1时刻参数粒子满足的均值和方差，并由式(2)更新状态粒子.

步骤3 权重更新:根据式(7)计算每个粒子的重要性权重，并归一化:

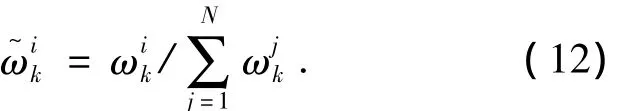
步骤4 重采样:消除重要性权重较小的粒子，复制权重较大的粒子，得到新的状态粒子.

步骤6 k＜M时，k=k+1，转到步骤2;k≥M时，循环结束.

3 仿真性能与分析

Wan和 Nelson在其文献 ［3］中提出用DEKF(双重卡尔曼滤波)方法分离混合信号，由于该方法能够有效去除系统噪声并分离出各路信号，在信号处理领域被广泛引用.针对非线性系统的情况，为了验证算法的有效性，笔者将本文算法与该文献算法进行了比较，对两路混合信号进行分离试验.

3.1 仿真模型

假设观测量yk由以下非线性系统状态空间模型产生:

3.2 仿真结果及分析

图1给出两种算法进行20次蒙特卡洛实验获得的参数估计平均值，这里设定观测时间k=2 000.

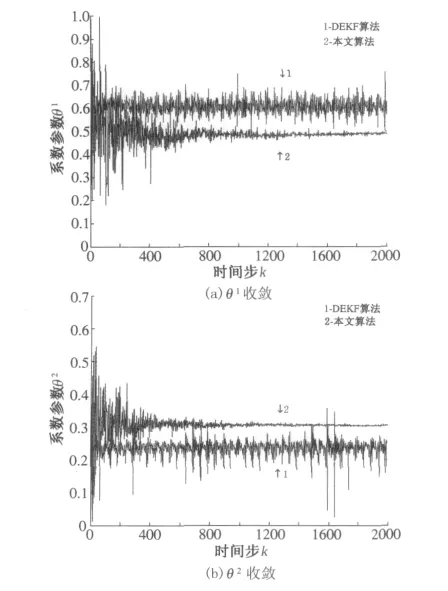
图1 系统参数θ1，θ2的收敛情况Fig.1 The convergence of the parameters θ1，θ2

结果表明，利用本文算法得到的系统参数估计值收敛于正确值0.5和0.3，而DEKF算法的系统参数在0.6和0.2附近上下摆动，无法收敛.表明本文算法使非时变参数估计的收敛性得到提高.

图2给出两路信号真实值与估计值的比较，设定观测时间k=100.

图2 x1，x2估计值与真实值的比较Fig.2 Comparation of true state and estimation values of x1，x2

仿真结果表明，与DEKF算法相比，笔者提出的算法能更好地与真实状态相吻合，表明本文算法能有效地分离混合信号.

为了对分离结果定量分析，表1给出经过100次Monte Carlo仿真实验，两种算法计算出的非线性系统中状态1和参数1以及状态2和参数2的RMSE均值.

表1 两种算法产生的状态x1，x2和参数θ1，θ2的经验标准偏差Tab.1 The mean square error of state x1，x2 and parameter θ1，θ2 produced by two algorithms

从仿真结果可以看出，本文算法的计算误差明显低于DEKF算法，表明本文算法能更准确地分离出两路信号状态和参数.

4 结论

为了对非线性非高斯系统进行混合信号分离，笔者提出了一种基于粒子滤波的分离方法，并采用核分布为贝塔分布的核平滑收缩技术来实现非时变参数的迭代.实验表明，本文算法在非线性系统中能有效的实现两路信号的分离，分离精度及收敛性均高于DEKF方法.

［1］ COWELL D MJ，FREEAR S.Separation of overlapping linear frequency modulated(LFM)signals using the fractional fourier transform ［J］.IEEE Transactions，2010，57(10):2324-2333.

［2］ NAMGOOK C，KUOC C J.Sparse music representation with source specific dictionaries and its application to signal separation［J］.IEEE Transactions，2011，19(2):326-337.

［3］ WAN E A，NELSON A T.Dual extended kalman filter methods in kalman filtering and neural networks［M］.New York:John Wiley and Sons Inc，2001:123-173.

［4］ DOUCET A，FREITAS J F G，GORDON N J.Sequential Monte Carlo Methods in Practice［M］.New York:Springer，2001:202-206.

［5］ OLSSON J，RYDEN T.Rao-Blackwellization of particle markov chain monte carlo methods using forward filtering backward sampling ［J］.IEEE Transactions，2011，59(10):4606-4619.

［6］ 王忠勇，冯卫娜.一种基于粒子滤波的非线性系统参数和状态联合估计方法［J］.郑州大学学报:工学版，2010，31(2):92-96.

［7］ 穆晓敏，曹丽果，路彦辉.一种新的基于粒子滤波的OFDM时变信道估计方法［J］.郑州大学学报:工学版，2011，32(2):84-87.

［8］ 刘凯，李辉.一种新的重叠混沌信号盲分离算法［J］.中国科学技术大学学报，2008，30(8):1129-1134.

［9］ WEST M.Approximating posterior distribution by mixtures［J］.Journal of Royal Statistical Society，1993，55(2):409-422.