改进型无网格迦辽金法在稳定热传导中的应用
夏茂辉,赵玉凤,吕 鹏,翟育鹏,任伟和
(燕山大学理学院,河北秦皇岛066004)
0 引言
近年来,无网格法已经发展成为一种功能较强、稳定性高的数值计算方法,而无网格迦辽金法(EFGM)是发展最为成熟的一种无网格法.传统的移动最小二乘法构造出一个近似函数[1],它的光滑性好且导数连续,其形函数及其导数仅与节点有关,但此方法容易导致系统方程病态,于是在此近似方案中采用带权的正交基函数,形成一种改进的移动最小二乘近似(IMLS).IMLS近似与EFGM相结合构成了IEFGM,该方法避免了矩阵求逆,且计算量小、数值稳定性好,不会形成病态方程组,因此有更高的计算速度和精度,在弹性力学和断裂力学中已得到了充分应用[2-5],但在温度场中还未得到深入研究.笔者在文献[6]的基础上对移动最小二乘近似进行改进,用IEFG法求解稳态热传导问题,并将其方法应用到矩形域和圆形域中,并与EFG法和精确解[7-8]进行比较,应用MATLAB编程将其结果进行可视化处理,表明该方法是一种收敛快、精度高、简便有效的方法.
1 移动最小二乘近似[1]
考虑点x的邻域Ωx,它位于全域Ω内,为求近似函数,在子域Ωx中随机分布有限个节点xi(i=1,2,…,n),函数 T 的近似表达式Th(x),∀x∈Ωx,可以定义为:

式中:PT(x)=[p1(x)p2(x)… pm(x)]是m次完备单项式的基;a(x)是包含系数ai(x),i=1,2,…,m的向量,这些系数是空间坐标x=[x y]的函数.对于二维问题:
线性基
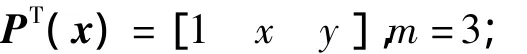
二次基

定义加权离散L2模为:

式中:wi(x)是节点i在x的权函数;Ti(i=1,2,…,n)是节点i处的名义节点值,一般它不是未知试函数Th(x)的节点值;n为插值基点数.
式(2)可用矩阵形式表达为:

其中,
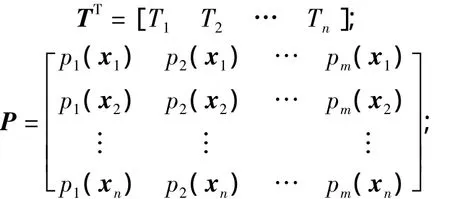

2 改进的移动最小二乘近似
在MLS近似中,式(4)有时是病态的,甚至出现奇异现象,而且难以得到数值解.为克服此缺点,采用 IMLS[2-5]近似.
对于∀f(x),g(x)∈span(p),定义
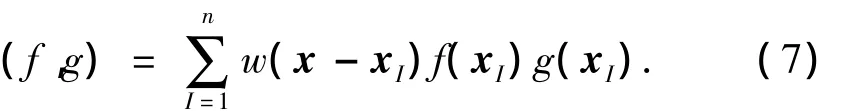
其中,span(p)是Hilbert空间;(f,g)是内积.对于一系列点{xi}和权函数{wi},若函数p1(x),p2(x)…pn(x)∈span(p)且满足:

所以由式(4)、式(7)可得:

其中,I=1,2,…,n.若 pi(x)∈span(p),i=1,2,…,m;(pi,pj)=0,i≠j,则(9)式为:
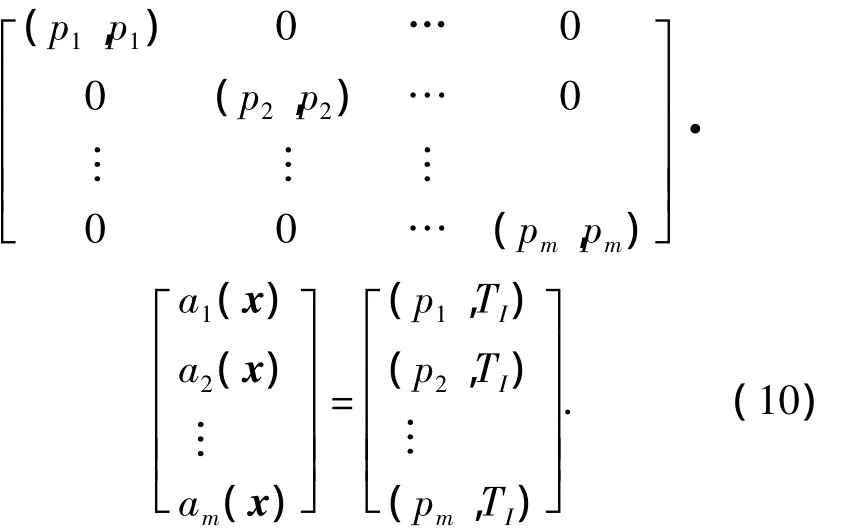
于是可得ai( x)为:

3 改进型EFG法(IEFGM)
考虑二维稳态热传导问题.
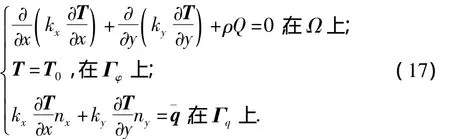
式中:T表示温度;T0为初始温度;Γφ为狄利克雷(Dirchlet)边界;Γq为诺依曼(Neumann)边界;ρ为材料密度;kx、ky是材料沿x、y方向的热传导系数;Q为物体内部的热源密度;nx和ny是边界外法线的方向余弦;¯q是给定的热流量.
与方程(17)相对应的弱形式为

把式(14)代入式(18),可得到离散方程:

由IMLS可得节点温度值

4 数值算例
算例1 圆域上的稳态热传导问题.考虑单位圆域上的稳态温度分布场,其控制方程为:

边界条件为:
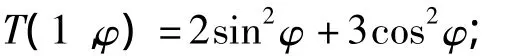
精确解的直角坐标表达式为[7]:

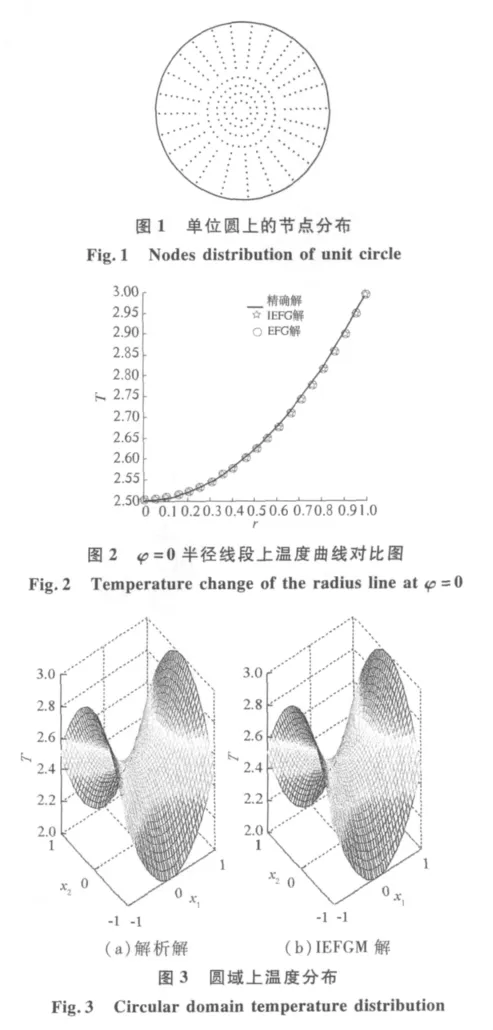
如图1在圆域内布置了120个规则节点,高斯积分背景网格与节点相重合,每个网格采用2×2高斯积分,采用三次样条权函数和带权的线性正交基函数.由IEFG法得直角坐标系下φ=0半径线段上温度曲线对比如图2,温度分布如图3,将改进型无网格迦辽金法(IEFGM)和精确解进行比较.
算例2 三维矩形域上的稳态热传导问题.立方体边长a=b=c=1,其控制方程和边界条件如下[8]:

采用均匀布点,布置945个节点对立方体进行离散(165个背景网格),影响域取为立方体影响域,每个背景网格内采用64个高斯积分点,权函数为三次样条权函数,二次正交基函数.图4为z=1时的温度分布对比图.图5为z=1时等温线对比图.将改进型无网格迦辽金法(IEFGM)和精确解进行比较.
由以上数值算例可以看出,通过IEFG法求解稳态热传导问题,结果比无网格迦辽金法精度高,和精确解高度吻合.得知IEFG法可以有效地用于求解矩形域和圆域内稳态热传导问题.
5 结论

(1)无网格迦辽金法仅需要布置节点,不需要划分单元,其结果与有限元高度吻合,而改进型无网格迦辽金法比迦辽金法有更高的精度和效率,且不会导致系统方程产生病态.
(2)尝试将改进的无网格迦辽金法应用到求解矩形域和圆域稳态热传导问题,有较好的精度和效率,且结果与精确解[7-8]高度吻合,在温度场中具有广泛的应用前景.
[1] 周晖,李勇.无网格伽辽金法在二维土体沉降分析中的应用[J].湖南科技大学学报:自然科学版,2009,24(2):53-56.
[2] 程玉民.移动最小二乘法研究进展与评述[J].计算机辅助工程,2009,18(2):5-11.
[3] ZHANG Zan,LIEW K M,CHENG Yu-min.Coupling of the improved element-free Galerkin and boundary element methods for two-dimensional elasticity problems[J].Eng Anal Boundary Elem,2008(32):100-107.
[4] 边燕飞.改进型无网格伽辽金法(IEFG)的研究及其应用[J].合肥工业大学学报:自然科学版,2009,32(4):32-35.
[5] ZHANG Zan,LIEW K M,CHENG Yu-min.Analyzing 2D fracture problems with the improved elementfree Galerkin method[J].Eng Anal Boundary Elem,2008,32:241-250.
[6] 高会生.MATLAB原理与工程应用[M].北京:电子工业出版社,2005.
[7] 商立英.非结构化网格上非稳态导热问题的求解与应用[D].南京:南京理工大学动力工程学院,2006.
[8] 陈琳.无网格在热传导问题中的应用[D].南京:南京理工大学动力工程学院,2009.

