基于Kriging模型的大客车侧翻安全性多目标优化
高云凯,张 朋,吴锦妍,王婧人
(同济大学 汽车学院,上海201804)
在所有交通事故造成的伤亡中客车侧翻造成的伤亡虽然比例不大,却经常出现“群死群伤”的结果,在社会上造成极大的影响,不利于社会的和谐与安定.为减少客车侧翻事故中的伤亡率,美国和欧洲先后制定了对客车上部结构要求的标准:FMVSS 216和ECE R66,前者规定了顶盖压垮试验中的车顶抗压强度,而后者要求客车进行侧翻试验,客车侧翻后要保持一定的乘员生存空间.我国依据ECE R66法规制订了《客车上部结构强度的规定(GB/T 14172—2009)》规定了客车上部结构强度的技术要求与试验方法.
在客车侧翻研究方面前人做了很多工作.金孟[1]建立了大客车的全板壳模型,并总结了大客车安全性研究的流程.Cezary Bojanowski等[2]建立了辅助客运巴士的有限元模型,按照FMVSS 220 和ECE R66两种法规进行了侧翻试验,与实车试验进行了对比,并通过优化客车上部结构的板厚来改善客车 侧 翻 安 全 性.Su 等[3]分 别 用RSM(response surface methodology)模型和RSM,RBF(radial bais function)混合模型拟合客车静态性能(刚度、应力)和侧翻性能,以侧翻安全性为约束,以质量最小、扭转刚度最大为目标,对板厚进行多目标优化.马林[4]运用响应面法优化了客车侧翻中的吸能状况.
以上文献大多是通过优化客车零部件的板厚来满足客车侧翻的安全性,同时实现轻量化的目标.本文拟通过优化客车重要零部件的截面形状来达到以上目标.本文建立了大客车的有限元模型并基于Kriging模型对客车侧翻安全性进行多目标优化,以客车上部结构中的关键部件截面形状为变量,在车体不侵入生存空间、生存空间不突出车体结构的前提下达到整车质量最小、质心加速度最小的目标.
1 客车侧翻安全性法规
为了便于衡量客车上部结构强度,ECE R66法规定义了“乘客生存空间”的概念.生存空间是一个位于车体结构内部贯穿乘客区和驾驶区并且与车体结构(变形之前)有着固定相对位置的空间,生存空间如图1所示.ECE R66法规[5]对客车上部结构强度的要求是:①处于生存空间外部的车体结构变形后不能侵入生存空间;②车体变形后生存空间不能突出到车体结构的轮廓面以外.
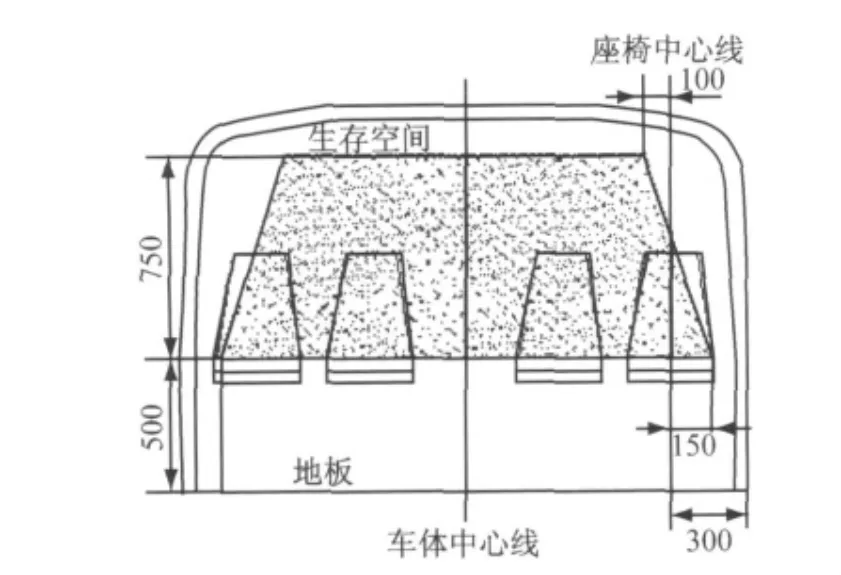
图1 生存空间尺寸与位置(单位:cm)Fig.1 Size and location of residual space(unit:cm)
2 客车有限元模型的建立
客车骨架主要由不同截面形状的薄壁管件焊接而成,在建模过程中对模型进行如下简化:忽略几何模型上的一些小尺寸倒角、小孔等几何元素;以共节点和刚性连接来模拟结构间的连接关系;用等效均布质量单元模拟发动机、座椅和地板等;不考虑骨架结构在焊接过程中出现的变形和残余应力;不考虑连接失效.
侧翻模型主要包括客车、翻转台和刚性墙(图2)三部分,其中客车骨架主要材料为Q235,采用DYNA 材料库里面的MAT24模拟,定义该材料密度为7.8×10-6kg·mm-3,弹性模量为2.1×105MPa,泊松比为0.3,屈服极限强度为210MPa.翻转台定义为刚体,并且限制其x,y,z向平动自由度,释放x向转动自由度.刚性墙则用关键字RIGID_WALL定义.

图2 客车有限元模型Fig.2 Finite element model of bus
ECE R66规定:侧翻试验中翻转平台离地距离为800mm,车身随平台以每秒不大于5°的角速度转动,直至侧翻至水泥地面.根据动能定理,由式(1)可算出客车与地面碰撞时的瞬时角速度.仿真试验的重力加速度g取9 800 mm·s-2.翻转平台与轮胎间的摩擦系数取0.4,其他位置的摩擦系数取0.3.
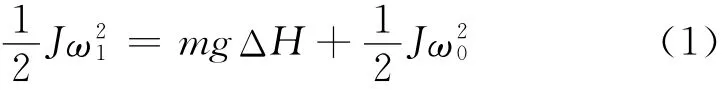
式中:J为客车绕翻转平台旋转轴线的转动惯量;ω1为客车落地瞬间的角速度;ω0为客车与翻转平台分离时的角速度;m为客车整车整备质量;ΔH为客车质心高度变化量.
3 初始模型分析与变量选取
根据ECE R66法规规定设定大客车侧翻仿真试验的初始条件,并利用LS_DYNA 进行计算,碰撞结果如图3所示.从图3中可以看出,碰撞结束后,生存空间穿出车体,说明侧翻中车身会挤压乘客造成威胁,需要对车身上部结构强化.
文献[6]提出一种生存空间的评价指标——生存空间评估角θ.分别选取右侧围前、后2根立柱与地板间的夹角θ1,θ2作为生存空间评估角(图4).
为减轻乘客与车体的二次碰撞,应该使车身在侧翻过程中加速度尽可能小,因此,以碰撞过程中车体的质心最大加速度a(以地板上某一靠近质心的节点最大加速度等效代替质心加速度)最小为优化目标,而这一指标的影响因素主要是客车碰撞过程中接地部分的刚度,即侧围的刚度.通过控制侧围立柱的截面尺寸来改变侧围刚度,从而实现不同的碰撞加速度.表1给出了原始模型侧翻试验中的各项指标.

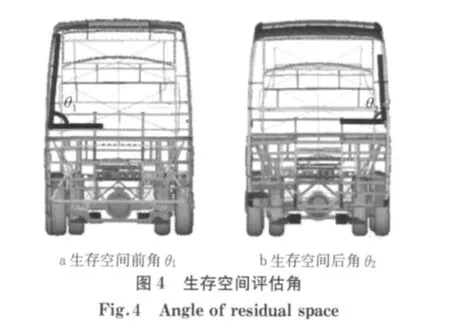
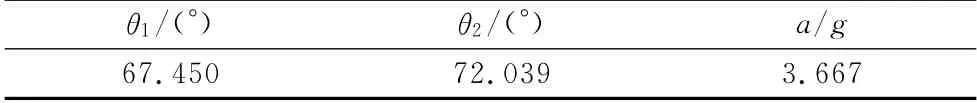
表1 原始模型侧翻指标Tab.1 Rollover index of initial model
如图5所示,客车侧围立柱(包括窗立柱和裙立柱)变形最大,侵入生存空间,不符合侧翻法规要求.客车侧翻与地面接触以后动能很大一部分被车体通过变形吸收转化为内能.因此,内能可以作为衡量变形的一个重要的标志.根据各部位吸能状况来选取设计变量.
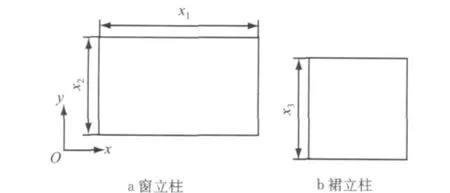
图5 形状变量Fig.5 Shape variables
参考表2中各部件的吸能状况,选取侧围立柱、窗立柱的截面形状作为优化变量.以车身坐标系为基准,侧围立柱与窗立柱截面的x向尺寸作为同一变量;侧围立柱和窗立柱的y向尺寸分别作为1个变量.最终选取3个变量.如表3所示.

表2 客车零部件吸能状况Tab.2 Energy absorption of bus components
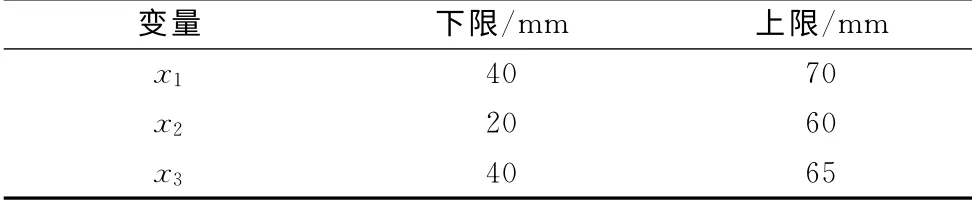
表3 变量的设计Tab.3 Design variables
4 近似模型
4.1 试验设计
为寻找最优生产条件或最优设计往往需要进行试验.而此类围绕验证最优生产和设计的试验是一项周期长、费用高的工作.正确的试验设计(DOE)能节约大量的人力、物力.常用的试验设计方法有全因素试 验 设 计(full-factor design)、正 交 试 验 设 计(orthogonal design)、拉丁方(Latin Hypercubes)试验设计和最优拉丁方(optimal Latin Hypercube)[7-9]试验设计.图6给出了设计示意图.
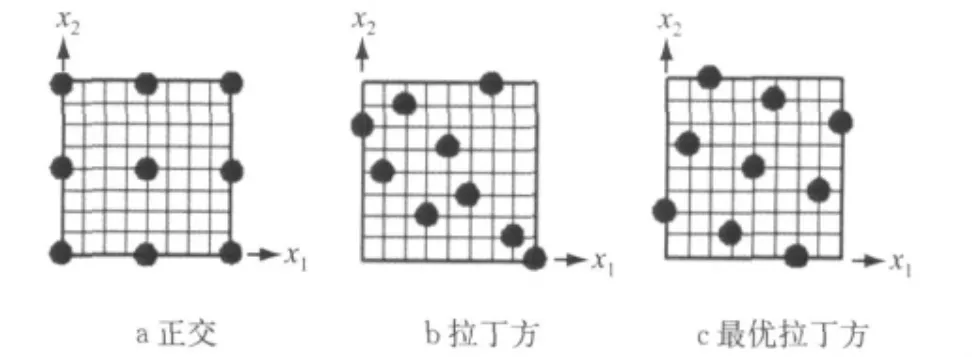
图6 三种试验设计方法对比Fig.6 Comparison of DOE methods
从图6中可以看出,正交试验只能取到所有因素各个水平中的3个,而拉丁方与最优拉丁方能取到9个,能尽可能利用样本点.拉丁方试验的样本点在设计空间的分布是随机的,即其列向量对应各变量在其范围内的随机取值,因此拉丁方试验不能均匀提取设计空间的特征,降低了近似模型的精度.最优拉丁方试验设计是根据优化准则优化拉丁方试验设计得到的.为使样本点均匀化,常用优化准则优化样本点,如熵准则、均方差和最小距离法等.最优拉丁方的样本点在设计空间分布均匀,更有利于生成精确的近似模型.文献[10]指出,均匀性越好拟合出的近似模型越精确,因此,采用最优拉丁方试验设计法选取3个变量,生成3×30的DOE 矩阵并生成模型.仿真计算后提取各个模型的变量与目标函数值.
4.2 Kriging模型
优化中有限元网格会产生穿透和单元质量问题,使得单次仿真失效而导致整个优化过程终止.用近似模型近似代替仿真模型进行优化可有效提高优化效率.同时,建立近似模型可以过滤有限元仿真造成的数值噪声.Kriging模型由全局近似模型与局部偏差结合而成[11].
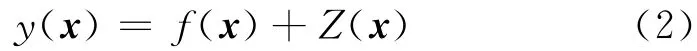
式中:y(x)为待拟合的响应函数,x为设计变量;f(x)通常是多项式响应面近似模型,一般被看作常数,提供设计空间的全局近似模型;Z(x)假设为高斯静态过程,其协方差为
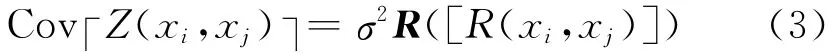
式中:Z(xi,xj)为均值为零的高斯静态随机过程;σ2为过程的方差;R(xi,xj)为相关函数;R为协方差矩阵,是一个n阶正定矩阵,n为样本点个数,其主对角线元素为1.文献[12]给出了Kriging模型的详细建模过程.根据表4 所示的30 个样本点生成Kriging模型.

表4 试验设计矩阵及响应值Tab.4 DOE matrix and response values
4.3 模型精度检验
对于设计目标t的n个数据点(t1,t2,…,tn)T有
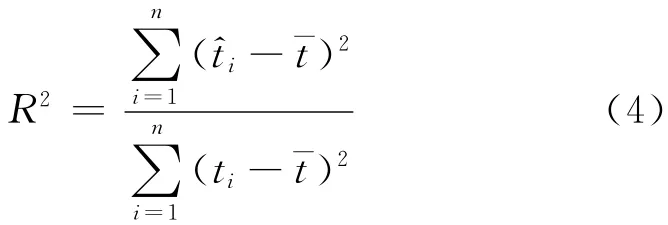
式中:t^i为设计目标的估计值;t-为设计目标的平均值;R2为决定系数,取值范围为[0,1],其值越接近于1说明拟合精度越高.Kriging模型是插值模型,因此需要通过6个额外的样本点来检验近似模型的精度(表5).根据Kriging模型预测值与仿真值算得质量增量、前角、后角、质心加速度的R2分别为0.997,0.981,0.998,0.927.各模型的R2都大于92%,满足工程要求.

表5 检验模型及其响应值Tab.5 Validation model and response values
5 优化
5.1 模型描述
针对初始车型侧围强度不足的情况,考虑轻量化及乘客与车身的二次碰撞,多目标优化的数学模型可以表述为
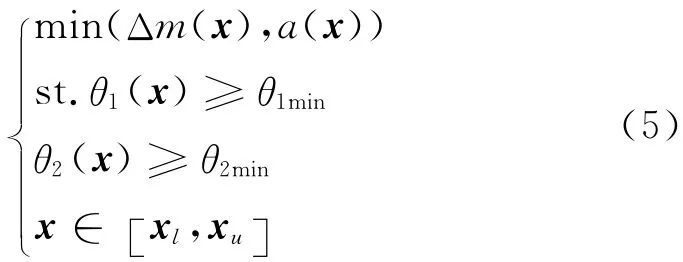
式中:Δm(x)为整车整备质量的增量;a(x)为侧翻中质心的最大加速度;θ1(x),θ2(x)为生存空间前角、后角;θ1min,θ2min为生存空间未被车身侵入时的前角、后角的最小值,θ1min=67.508°,θ2min=72.510°;x=[x1,x2,…,xn],xl,xu分别为x的下限和上限.
5.2 NSGA-II算法
NSGA (non-dominated sorting genetic algorithm)算法由Srinivas等于20 世纪90 年代初期提出,它是基于个体等级按层次来分类的[13].该算法首次将非支配排序法引入多目标优化,使多目标简化至1 个适度函数.但NSGA 本身存在不足之处[14]:①计算复杂性较高;②缺乏精英策略;③需要特别指定共享半径.
NSGA-II算法[15]是在NSGA 算法的基础上进行改进的多目标算法.NSGA-II算法引入了精英策略、密度值估计策略和快速非支配排序策略,其计算流程如图7.
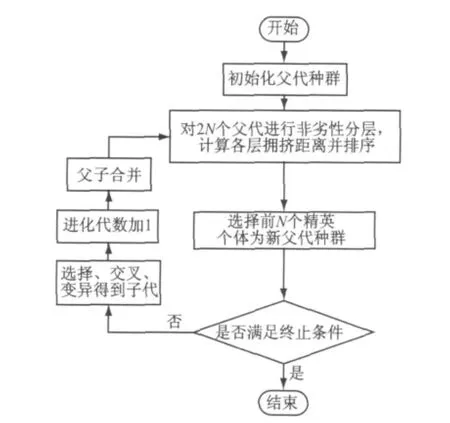
图7 NSGA-II算法流程Fig.7 Flowchart of NSGA-II
5.3 优化结果
关于Pareto前沿,有如下定义[16]:
(1)Pareto支配关系.设p,q为进化种群中的任2个不同个体,①对于p和q及任意子目标函数fk(x),有fk(p)≤fk(q);②至少存在1个子目标函数fl(x),使fl(p)≤fl(q)(k,l=1,2,…,r),r为子目标的数量,则称p为支配的,q为被支配的,记作p≻q.
(2)Pareto优化解集.决策变量x∈Xf(Xf为可行域)相对于集合A⊆Xf被称为是非支配的,当且仅当a∈A:a≻x,如果相对于可行域Xf决策变量x是非支配的,则称x为Pareto优化解.所有优化解构成了Pareto优化解集,即Pareto前沿.
设置NSGA-II个体数为100、迭代代数为200.图8是优化得到的Pareto前沿.依据设计人员的偏好、工程应用的经济性等选取最优解.选取Pareto前沿中的3个解(图8标方框处)生成模型进行计算.其中第1个解侧重于车身的轻量化,第2个解兼顾侧翻加速度与车身质量,第3个解偏于安全性.
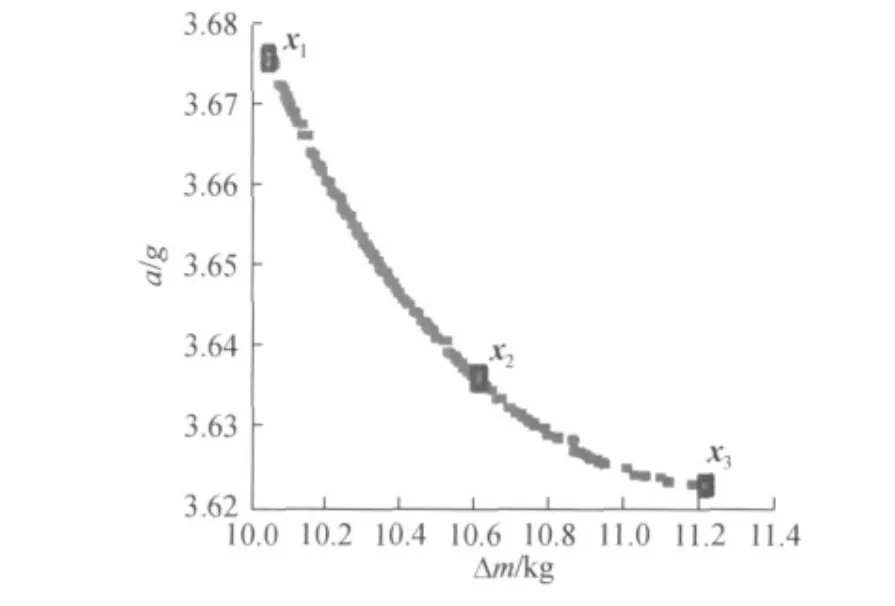
图8 Pareto前沿Fig.8 Pareto front
以表6中的第2组解为例,对比原始模型优化模型质量增加了0.738%(10.6kg),但是侧翻安全指标(生存空间角和质心加速度)均得到改善,生存空间评估角前角增加了0.532°,后角增加了0.471°,相当于侧翻中车身与生存空间的最小距离增加了11 mm(前角处)和10 mm(后角处).根据Pareto解集生成实车模型并进行侧翻试验(图9),生存空间与车体的最小距离为13mm,满足ECE R66法规要求.
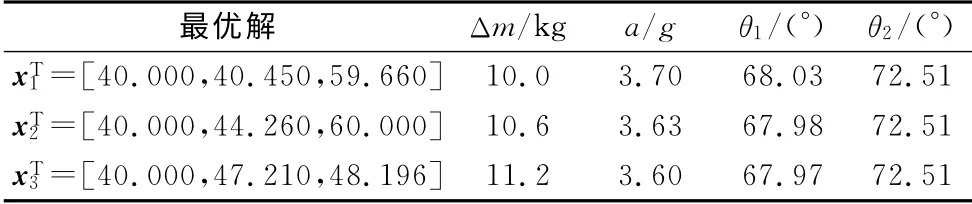
最优解 Δm/kg a/g θ1/(°) θ2/(°)xT1=[40.000,40.450,59.660]10.0 3.70 68.03 72.51 xT2=[40.000,44.260,60.000] 10.6 3.63 67.98 72.51 xT3=[40.000,47.210,48.196]11.2 3.60 67.97 72.51

图9 客车实车侧翻试验Fig.9 Physical test of bus rollover
6 结语
(1)通过改变截面形状优化大客车的侧翻安全性.相对于板厚,截面形状对客车的质量影响较小.当车身强度不足时,使用优化截面法能提高整车的侧翻性能而使整车质量增幅较小.
(2)最优拉丁方法提高试验设计的均匀性,拟合出高精度的近似模型.
(3)结合Kriging模型和NSGA-II算法提出解决多目标形状优化的方法,并将其成功应用于客车侧翻的多目标优化,给出了Pareto最优化解集,供设计人员参考.
[1] 金孟.客车翻滚安全性研究及流程开发[D].上海:上海交通大学,2009.JIN Meng.Research on bus rollover safety and process development[D].Shanghai:Shanghai Jiao Tong University,2009.
[2] Cezary Bojanowski,Broislaw Gepner,Leslaw Kwasniewski,et al.Roof crush resistance and rollover strength of a paratransit bus[C]∥8 th European LS-DYNA Users Conference.Strasbourg:[s.n.],2011:1-13.
[3] Su R Y,Gui L J,Fan Z J.Multi-objective optimization for bus body with strength and rollover safety constraints based on surrogate models[J].Structural and Multidisciplinary Optimization,2011,44(3):431.
[4] 马林.基于响应面法的全承载大客车侧翻安全性多目标优化[D].北京:清华大学,2009.MA Lin.Multi-objective optimization for rollover safety of a fully integral bus based on RSM [D].Beijing:Tsinghua University,2009.
[5] United Nations.ECE regulation No.66 Uniform technical prescriptions concerning the approval of large passenger vehicles with regard to the strength of their superstructure[S].[S.l.]:United Nations,2006.
[6] 何汉桥,张维刚.高床大客车侧翻结构安全性仿真研究[J].机械科学与技术,2007,26(7):922.HE Hanqiao,ZHANG Weigang.Simulation of safety of highbed bus under side overturning crash[J].Mechanical Science and Technology,2007,26(7):922.
[7] 赵敏,钟志华,王国春,等.基于正交试验设计的微型轿车侧撞安全性研究[J].汽车工程,2010,32(5):409.ZHAO Min,ZHONG Zhihua,WANG Guochun,et al.Research on the lateral crashworthiness of a mini car based on orthogonal experimental design[J].Automotive Engineering,2010,32(5):409.
[8] 刘晓路,陈英武,荆显荣,等.优化拉丁方试验设计方法及其应用[J].国防科技大学学报,2011,33(5):73.LIU Xiaolu, CHEN Yingwu, JING Xianrong, et al.Optimized Latin Hypercube sampling method and its applicetion[J].Journal of National University of Defense Technology,2011,33(5):73.
[9] 方开泰.均匀设计与均匀设计表[M].北京:科学出版社,1994.FANG Kaitai.Uniform design and uniform design table[M].Beijing:Science Press,1994.
[10] 李响,李为吉,彭程原.基于均匀实验设计的响应面方法及其在无人机一体化设计中的应用[J].机械科学与技术,2005,24(5):575.LI Xiang,LI Weiji,PENG Chengyuan.Response surface methodology based on uniform design and its application to complex engineering system optimization [J].Mechanical Science and Technology,2005,24(5):575.
[11] Simpson T W, Mistree F. Kriging models for global approximation in simulation-based multidisciplinary design optimization[J].AIAA Journal,2001,39(12):2233.
[12] 高云凯,孙芳,余海燕.基于Kriging模型的车身耐撞性优化设计[J].汽车工程,2010,32(1):17.GAO Yunkai,SUN Fang,YU Haiyan. Crashworthiness optimization of car body based on Kriging surrogate model[J].Automotive Engineering,2010,32(1):17.
[13] Srinivas N,Kalyanmoy Deb.Multi-objective optimization using nondominated sorting in geneticalgorithms[J].Evolutionary Computation.1994.2(3):221.
[14] 张晓菲,张火明.精英策略的改进非支配遗传算法[J].中国计量学院学报,2010,3:53.ZHANG Xiaofei, ZHANG Huoming. Improved nondominated sorting genetic algorithm II based on the elitist strategy[J].Journal of China University of Metrology,2010,3:53.
[15] Deb K,Agrawal S,Pratap A,et al.A fast elitist nondominated sorting genetic algorithm for multi-objective optimization:NSGA-II[C]//Parallel Problem Solving from Nature PPSNVI.Berlin:Springer,2000:849-858.
[16] 关志华,寇纪淞,李敏强.一种改进的非支配排序遗传算法INSGA[J].天津大学学报,2002,35(4):429.GUAN Zhihua,KOU Jisong,LI Minqiang.An improved evolutionary algorithm for multi-objective optimization[J].Journal of Tianjin University,2002,35(4):429.

