基于欧氏距离的基本信任函数确立方法
党常会,朱海潮,章林柯,聂永发
(1.海军工程大学 振动与噪声研究所,湖北 武汉430033;2.中国人民解放军92646 部队,辽宁 大连116504)
0 引 言
声学故障是导致舰船声隐身性能恶化的重要因素[1]。基于案例推理(Case-Based Reasoning,CBR)的专家系统是一种解决声学故障检测定位以及修复问题的重要工具。在案例推理技术中,利用案例相似性进行类比推理是一个不确定性推理过程;在多种信息源的情况下,经案例推理会得到多个诊断结果,不利于操作者决策。为此,需要研究信息融合技术以实现以下目标:①综合利用各种数据信息进行推理,提高诊断声学故障的精确性;②给出统一的诊断结果以方便声学故障修复决策。
信息融合技术按照融合的层次可分为3 种融合方式:数据级融合、特征级融合和决策级融合。在案例推理技术中,当存在多个振动传感器数据输入的情况下,需要对各个传感器数据经案例推理之后的输出结果进行融合,以给出高置信度和统一的诊断结果。这实质上是一个决策级融合的过程。
常用的信息融合方法有贝叶斯概率推理法及D-S 证据理论等[2]。贝叶斯概率推理理论基础完备,但使用过程中需要事先明确事件发生的先验概率,而事件发生的先验概率在现实中很难得到。D-S 证据理论为不确定信息表达和合成提供了一套完整的方法,因此在信息融合领域得到广泛应用。
在D-S 证据理论应用过程中,基本信任分配函数确定是一个难题。基本信任函数确定方法主要有3 种:
1)基于专家经验[3],即基本信任函数由相关领域内的专家根据经验给出。该确定方法受人为因素影响较大,不同专家给出的基本信任函数值相差较大。
2)基于模型法[4],即考虑传感器对目标模式的相关系数、传感器、环境等影响因素来构建基本信任分配函数。但这些影响因素具体数值是很难确定的。
3)基于统计概率的方法[5-6],即利用训练样本统计故障模式发生的概率,然后确定基本信任分配函数值。有些人采用神经网络与D-S 证据融合相结合的方法[7],避免了对基本信任函数的确定问题。这些方法受样本数量的影响,样本量很小时得到的结果误差将很大。在案例推理技术中,新案例与源案例之间的相似性包含了基本信任度的信息[8],因此可以利用案例相似性确定基本信任分配函数。这是本文的主要研究内容。
1 D-S 证据理论
假设识别框架Θ 下的2 个证据分别为E1和E2,其相应的基本信任分配函数为m1和m2,焦元分别为Ai和Bj,则D-S 合成规则[9]为
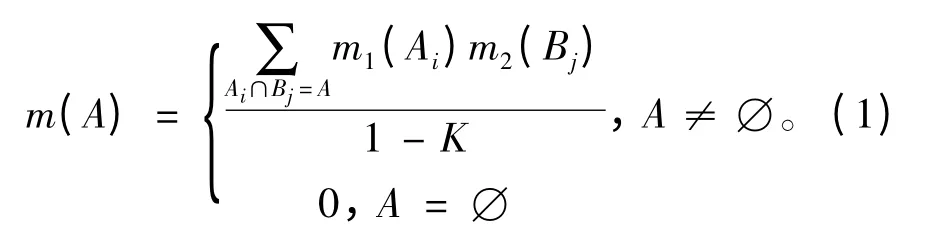
2 基本信任函数确定方法
在案例推理过程中,新案例与案例库中的案例之间的相似度是区分新案例所属类别的重要参数。相似度越大,新案例属于案例库中某案例的可能性就越大;反之,相似度越小,新案例属于该案例的可能性就越小。为此,可以利用相似度来构建基本信任分配函数值。
常用的衡量案例之间相似度的指标包括距离度量法、测度度量法等。在案例推理中,一般采用距离度量的方法。常用的距离度量参数有欧氏距离和Mahalanobis 距离等。在此,选用欧氏距离作为相似度的度量参数。假设2 个案例分别用向量x1和x2表示,那么2 个案例x1和x2之间的欧氏距离为:
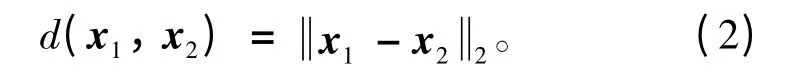
欧氏距离反映了案例之间的相似性:距离越大,相似性越小;距离越小,相似性就越大。
从样本分布的角度来说,离案例库中源案例的距离越小,该模式对应的样本概率密度就越大;离源案例距离越远,该模式对应的样本概率密度就越小。因此,某模式下样本的概率密度与欧氏距离密切相关。这个概率密度可以通过统计大量的试验样本数据而得到,而实际上样本数据数量是有限的,因此通过大量试验获取概率密度是不现实的。为了获得某样本模式在欧氏几何空间各点处分布的概率密度,本文引入一假设:假设新案例样本的概率密度与离源案例中心之间的距离r 的a 次方成反比,用数学式表示为

式中a 反映了样本分布概率密度以及与源点之间的欧氏距离的比例关系。当a=2 时,说明样本概率密度分布与以源案例所在点为球心所构成的球形表面积成反比;当a=3 时,则说明样本概率密度分布与以源案例所在点为球心所构成的球的体积成反比。式(3)能解释“离样本模式点越远,样本概率密度就越小”的现象,说明这种假设在案例推理技术中是满足使用要求的。
由传感器获得的新案例可能是案例库中任何一个案例的信任度就取决于各源案例在新案例所在位置处的贡献大小。假设案例库中有n 个代表不同样本模式的案例,描述这些案例的特征向量分别为x1,x2,…,xn。新案例对应的特征向量为x0。di(i=1,2,…,n)表示新案例与案例库中第i 个案例之间的欧氏距离,可利用式(2)求取。p(i)表示案例库中第i 个案例在新案例所处位置处的概率密度,通过式(3)求取。那么,新案例隶属于案例库中第i 个案例的概率为

这样就构造出了D-S 证据理论中所需要的基本信任分配函数。
由基本信任分配函数计算式(4)可知,新案例与案例库中某案例之间的欧氏距离越小,那么利用上述公式所得到的基本信任分配函数值就越大,即新案例属于该案例的信任度就越大。当新案例与案例库中某案例之间的欧氏距离为0 时,利用上述公式所得到的基本信任分配函数值为1,可以认为新案例完全属于案例库中某案例。这与“欧氏距离越小,相似度就越高”所得到的结论是一致的。
3 实验研究
D-S 证据理论在案例推理技术中进行决策级融合的过程图如图1所示。

图1 多传感器信息时案例推理过程示意图Fig.1 Process of CBR for multi-sensors
为了验证上述方法的可行性,可设计了一个试验。试验采用1 个壳体模型,内部布置由海水泵、伺服电机、管路、隔振装置等。传感器采用2 个振动加速度传感器,分别布置在泵体上、伺服电机基座处。设计工况分为正常工况和故障工况2 种。此故障工况是指通过调整海水系统出口阀门大小来模拟海水系统偏离设计工况,模拟发生了声学故障。利用数据采集系统分别采集2 种工况下的振动信号,采样率为2 048 Hz,每个工况采集数据时间为8 s。取前5 s 数据作为训练样本,取后3 s 数据作为测试样本;每个样本为1 s 数据(数据长度为2 048 个点),经特征计算与提取后,选择时域特征中的均值、方差、标准差3 个参数作为描述海水泵运行状态的数据特征。
1)案例表示
对训练样本进行学习所获得的源案例,如表1所示。
取工况1 时的1 个测试样本,如表2所示。
2)计算基本信任函数
利用通过传感器1 和2 的数据获得的新案例,分别计算新案例与源案例之间的欧氏距离。然后利用方程(4)计算基本信任函数值(在此取a=2),所得结果如表3所示。

表1 案例库中源案例Tab.1 Source cases in database

表2 通过传感器获得的新案例Tab.2 New cases obtained by sensors
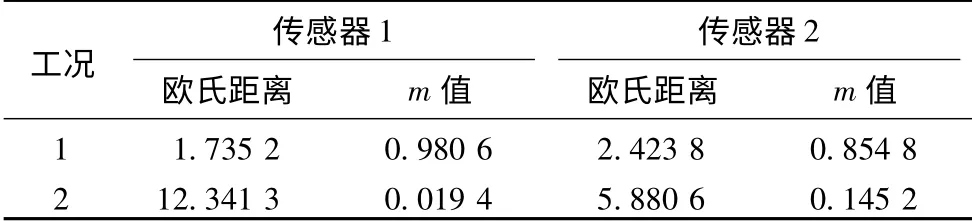
表3 基本信任函数计算结果Tab.3 Results of mass function
3)利用D-S 证据理论进行信息融合
将利用传感器1 和2 获得的基本信任函数值代入式(1)进行证据组合,得到的新信任函数值为:m(工况1)=0.996 7,m(工况2)=0.003 3。结果表明,新工况99.67%的可能性是工况1,而0.33%的可能性是工况2。从而得到最终结论:新工况属于工况1。这样就解决了2 个传感器信息的融合问题,验证了方法的可行性。
4 结论与展望
本文以基于案例推理技术解决声学故障定位问题为研究背景,利用样本之间的欧氏距离构建了基本信任函数,解决了在案例推理技术中利用D-S 证据理论进行信息融合所面临的确定基本信任函数的问题。经研究得到以下结论:
1)针对D-S 证据理论中基本信任函数很难确定的问题,文中根据样本随欧氏距离概率分布模型假设,提出了1 种构造基本信任分配函数的方法。实验证明该方法是有效的。
2)文中提出的基本信任函数确定方法具有模型清晰、计算方便的特点,适用于在案例推理方法中解决信息融合问题。
D-S 证据理论在案例推理技术实际使用过程中还会遇到证据冲突问题、证据之间的相关性问题等,还需要作出相应的处理以提高案例推理结果的精确性。
[1]章林柯.声学故障识别技术及其应用研究[D].武汉:海军工程大学,2006.
[2]MAKSYM J N.Expert systems for ship noise interpretation[J].Adaptive Methods in Underwater Acoustics,1985.653-670.
[3]王帆,李绪志.故障树和证据推理结合的故障诊断技术[J].微计算机信息,2007,23(25):165-167.WANG Fan,LI Xu-zhi.Fault diagnosis system based on fault tree and evidence reasoning[J].Microcomputer Information,2007,23(25):165-167.
[4]黄瑛,陶云刚.D-S 证据理论在多传感器数据融合中的应用[J].南京航空航天大学学报,1999,31(2):172-177.HUANG Ying,TAO Yun-gang.Implementation of D-S evidential theory in multisensor data fusion system[J].Journal of Nanjing University of Aeronautics &Astronautics,1999,31(2):172-177.
[5]李进,赵宇,黄敏.基于决策级数据融合的可靠性综合验证方法[J].北京航空航天大学学报,2010,36(5):576-579.LI Jin,ZHAO Yu,HUANG Min.Reliability integrated compliance testing plans based on decision making level data fusion[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(5):576-579.
[6]蓝金辉,马宝华,蓝天,等.D-S 证据理论数据融合方法在目标识别中的应用[J].清华大学学报(自然科学版),2001,41(2):53-55,59.
[7]耿立恩,潘旭峰,李晓雷,等.Dempster-Shafer 证据推理在数据融合中的应用[J].北京理工大学学报,1997,17(2):198-205.
[8]李玉榕.信息融合与智能处理的研究[D].杭州:浙江大学,2001.LI Yu-rong.Research on information fusion and intelligent process[D].Hangzhou:Zhejiang University,2001.
[9]杨风暴,王肖霞.D-S 证据理论的冲突证据合成方法[M].北京:国防工业出版社,2010.

