改进的灰色模型在船闸通过量预测中的应用

王 馨 陶桂兰 杨 正

（河海大学港口、海岸与近海工程学院 南京 210098）

船闸通过量预测是船闸扩容改建工程的决策依据和规划基础．常用的船闸通过量预测方法很多，如线性回归法、弹性系数法、三次指数平滑法、灰色GM（1，1）模型等．各方法总体思想大致相同，以多年特征数据为基础，运用线性或非线性增长函数或模型进行定量预测．前两种方法是一种相关因素分析预测方法，后两种是数据序列预测方法．船闸通过能力影响因素众多，常规的预测方法并不能涵盖所有因素的影响；三次指数平滑法虽然精度较高，预测终值趋于平稳，但始终只是单一数据量分析，不能反应其他因素的影响情况，并且当原模型数据少时，准确性越低．灰色模型，虽然也是数据量分析，但由于它分布显示概率特性，以及本身的模糊性，可通过少量数据进行预测，建模过程简单，模型表达式求解容易，应用日趋广泛．

灰色模型进行短期预测精确度较高，但中长期预测效果并不好，有可能出现预测值偏大的结果．这主要与灰色模型的序列光滑度有关．当原始序列越平缓，模拟值精度较高．反之，模型偏差较大，通常无法用于中长期预测，甚至不宜作短期预测［1］．

本文对灰色GM（1，1）模型进行了改进，通过函数变换改变序列的光滑度，以积分逼近值代替均值提高发展系数精度，从而得到了比原GM（1，1）模型模拟精度高和适用范围更广的新模型．

1 灰色模型介绍

1．1 GM（1，1）模型

灰色模型预测是在数据不呈现一定规律下可以采取的一种建模和预测方法，其预测数据与原始数据存在一定的规律相似性．灰色模型尤其适用于存在不确定性和未知因素的动态预测．最简单最常用的灰色模型为GM（1，1）模型．其主要理论是以灰色模块为基础，通过数据处理和微分拟合，进行动态预测．GM（1，1）模型如下．

1）建立原始时间序列

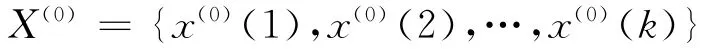
2）初始数据处理 对原始数据进行一次累加，形成新的时间序列，记1－AGO，为

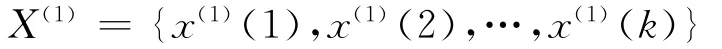
其中：k为原始数据个数；

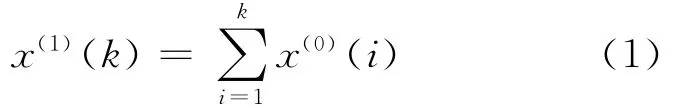
3）建立灰色微分方程

一阶微分方程又称白化方程，积分后可得到灰色模型

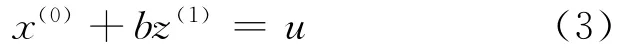
式中：b为模型的发展系数；u为待定系数；z为1－AGO序列相邻时间间隔内的增长量，其值为

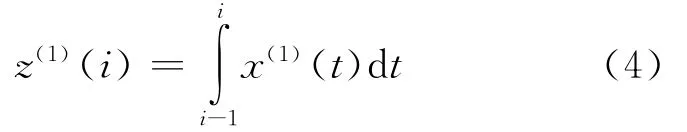
4）函数求解 为简化计算，假定相邻时间间隔内无突变，以均值代替积分值，取Z（1）为

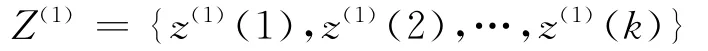
式中：

假定φ为待辨识参数向量，可由最小二乘法求得

式中：

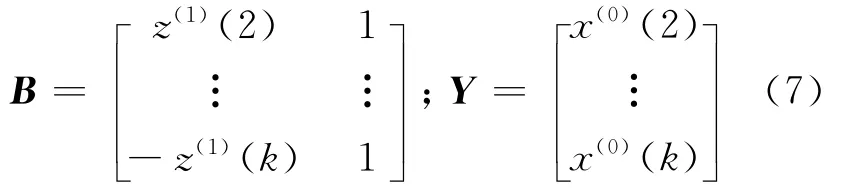
解微分方程得到灰色微分方程的时间响应函数为

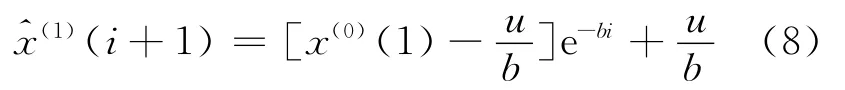
5）预测方程 经过累减，进行数据还原可以得到原序列的预测值

1．2 GM（1，1）模型的改进

传统的灰色GM（1，1）模型短期预测精确度较高，但中长期预测效果并不好，有可能出现预测值偏大的结果．这主要与灰色模型的序列光滑度有关．一般地，通过指数函数变换、幂函数变换、指数函数、幂函数复合变换，将初始序列变换为1－AGO序列，使序列变化趋于平缓，从而提高序列光滑度．

此外，从时间响应函数的解的形式可以看出，方程解的精度实际上取决于发展系数b的取值，而b的取值与相邻时间间隔增长量z密切相关．由于假定数据在相邻时间间隔内无突变，以均值代替z的积分值的办法简化计算，当发展系数取值较小时，传统模型预测值满足精确要求，若发展系数偏大，则传统模型不再适用．文献［2］通过z值处理，即用积分逼近真实值代替均值计算相邻时间间隔增长量z，来拓展发展系数b的取值范围．经过传统模型与z值处理模型在不同发展系数下的拟合精度比较，验证了z值处理后的模型可提高b的取值范围，从而增强模型的适用性．

本文采用幂函数变换对初始数列处理，同时以积分逼近值代替均值提高发展系数取值，从而得到了比原GM（1，1）模型模拟精度高和适用范围更广的新模型．

1）原始序列处理 引入幂函数a－xm（a＞1，m＞1），将x（0）进行幂函数变换，得到新的序列x（1），对于序列x（1），累加得到1－AGO 序列x（2）．从幂函数的形式可以看出，不同的a和m 的取值，会产生不同的新序列，从而得到不同的预测模型．文献［3］经过数学定理验证了只要满足a＞1，m＞1，幂函数即为光滑离散函数，通过相应的幂函数变换提高序列的光滑度．为得到效果较好的预测模型，通常采用试算的方法，通过多次数据拟合，选定一组使得预测模型拟合精度较好的a和m值，从而确定幂函数的形式，进行幂函数变换．

2）z值积分逼近 文献［4］从灰色模型原理出发，认为一切经过累加后的序列，均以指数形式增长．将x（2）以指数时间函数拟合，即：x（2）（t）＝B eAt，经过累加变化，得到从而得到z（i）的积分逼近值为

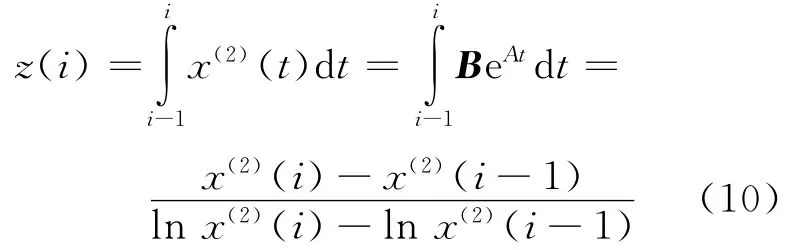
3）预测方法 重复前节所述步骤，得到模型响应函数，求解即得到幂函数变换序列下的预测值．然后通过指数－对数还原，得到原始序列下的预测值．

2 实例验证

本文采取苏北运河1990年至1996年累积货物通过量作为原始数据，分别建立原始预测模型和本文改进预测模型，运用自编matlab程序计算，预测1997年至2001年货运量．为叙述方便，下文分别记为原始模型、新模型．

2．1 响应函数

本文通过初始数据幂函数变换、z值处理和函数响应，建立改进的GM（1，1）模型，即新模型．经过多次数据拟合，选取a取1．14，m取1．06，可以平均相对误差绝对值最小，模型精度最高．经过幂函数变换后的数据所拟合的灰色方程的响应函数为

原始模型时间响应函数为

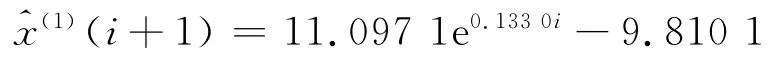
2．2 模型检验

建立的预测模型是否合理，预测结果的精度是否满足要求，通常采用原点检验法检验．原点检验法即以相对误差绝对平均值来反映原始数据与拟合数据的接近程度，一般地，当相对误差绝对平均值小于5%时，可以认为模型误差合格．

经过函数响应，得到原始模型和新模型的预测结果，现通过原点检验法检验模型的合理性和精度．两模型拟合量及误差分析见表1．各模型的相对误差绝对平均值在允许范围内，其建立的拟合曲线可以作为预测曲线使用．

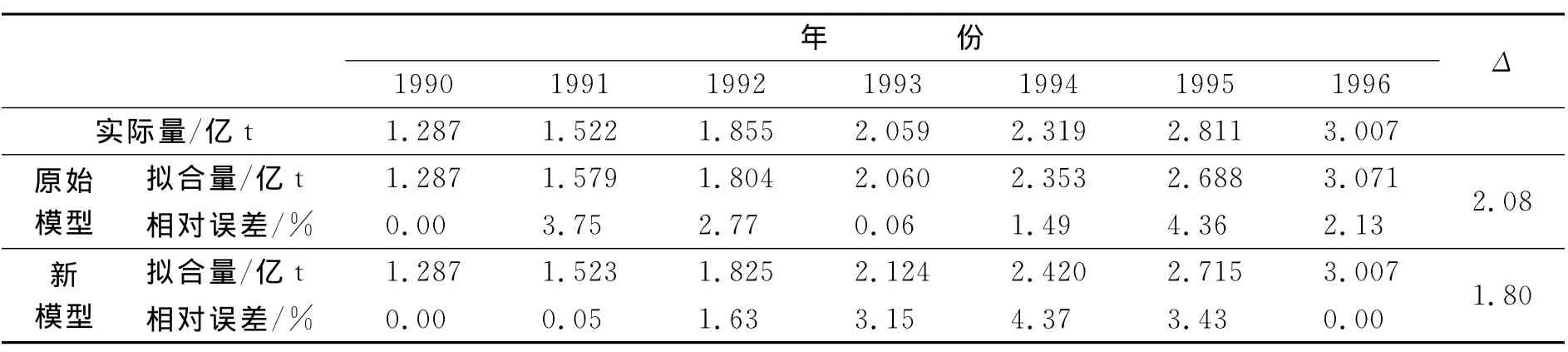
表1 模型拟合量与误差比对表

2．3 模型预测

运用原始模型和新模型预测1997～2009年苏北运河船闸累积货物通过量．1997～2001年为短期预测，预测结果见表2；2002～2009年为中长期预测［5－7］，预测结果见表3．

2．4 模型精度分析

现绘出模型短期预测曲线与实际量曲线比对图（见图1），结合上节各拟合、预测表，可以得出以下结论：（1）两模型拟合值关联度较好、相差不大，而预测值差异很大．从预测结果来看，新模型无论短期预测还是中长期预测，预测结果比较接近实际值，而原始模型预测值与实际值差异较大．2001年原始模型预测量超过实际量40%以上，原始模型短期预测效果并不理想．而2009年预测结果来看，原始模型预测量与实际货运量的比值达到220%，原始模型基本不适用于中长期预测；（2）原始模型拟合量相对误差绝对平均值为2．28%；而新模型拟合量相对误差绝对平均值为1．80%．后者误差平均值较前者减小了约1／5；（3）从短期预测曲线来看，新模型预测曲线较为平缓，且接近实际量走势线；原始模型预测曲线较陡，偏离实际值走势线．

表2 1997～2001年苏北运河船闸累积货物通过量亿t

表3 2002～2009年苏北船闸累积货物通过量 亿t

显然，新模型预测结果较好、精度较高、适用范围更广．这是由于新模型结合了幂模型和z模型的改进特性，不仅预测结果趋于平稳、接近实际值，又有效提高了模型精度、增强了模型适应性．

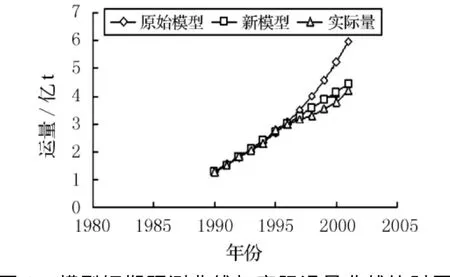
图1 模型短期预测曲线与实际运量曲线比对图

3 结束语

由表3可见，自2004年起苏北船闸累积货运实际量比新模型预测量偏高．这是由于“十一五”期间，苏北10个梯级船闸陆续开展了扩容改造工程建设，苏北船闸累积货物通过量明显提高．由于新模型以1997年以前数据为原始数据，未能及时反映数据变化新特性，新模型预测量偏于保守．在实际船闸工程货物通过量预测中，还要充分考虑国民经济发展趋势，结合其他预测方法的结果，综合考量，确定合理的预测量．

综上所述，新模型既适用于短期预测，又适用于中长期预测，可以作为船闸货运量预测模型广泛应用于实际工程中．

［1］吴春广．灰色预测模型的进一步改进［J］．赤峰学院学报：自然科学版，2008，24（5）：5－7．

［2］罗 党，刘思峰，党耀国．灰色模型 GM（1，1）优化［J］．中国工程科学，2003，5（8）：50－53．

［3］陈 洁，许长新．改进的灰色模型在港口吞吐量预测中的应用［J］．水运工程，2005（1）：20－23．

［4］何 斌，蒙 清．灰色预测模型拓广方法研究［J］．系统工程理论与实践，2002（9）：137－140．

［5］钱 芳．水运量预测方法与应用［D］．南京：河海大学交通学院，2006．

［6］文 军．基于灰色马尔可夫链模型的航空货运量预测研究［J］．武汉理工大学学报：交通科学与工程版，2010，34（4）：695－698．

［7］宋中民．灰色区间预测的新方法［J］．武汉理工大学学报：交通科学与工程版，2002，26（6）：796－799．