近景运动目标的单经纬仪定位方法

付晓伟，普仕凡，宋 蕾

（解放军91550部队，辽宁 大连 116023）

0 引言

经纬仪是航天测控中的重要定位设备。为了描述目标运动轨迹，对于地球上已给定的坐标系，需要测定目标运动过程各时刻在该坐标系下的坐标，即在各时刻对目标进行空间定位。采用经纬仪等光学设备进行目标定位，是一种精度较高的定位方法。传统的光学定位方法有交会定位与测距定位，但交会定位需要两台或两台以上的经纬仪，而测距定位虽然是单机定位，但需要增加测距信息，这在实际测控中很难实现［1－4］。本文则是探索除了上述两种方法之外的另一种新的方法，即在近景拍摄的特殊条件下，不需要增加测距信息而完成单机定位。

1 传统定位方法

对于飞行目标的空间定位，传统的光学定位方法认为目标只是一个点，这和目标飞行到远处的情况相吻合。而当目标在近处时，其细节特征被忽略，仍然只选择一个特征点进行观测，即目标整体始终被看作一个点目标。

1.1 交会定位

交会定位方法是基于两台经纬仪交会的双目视觉原理，要求两台经纬仪必须同时对准目标，形成交会。每台经纬仪分别测得方位α、俯仰γ两个角度信息，在假定坐标系下，由已知四个测量信息αi、γi（i＝1，2）与未知量的三维坐标（x，y，z）T建立观测方程，可用最小二乘法求解。这是一种常用方法，并以此为基础发展为多台经纬仪交会的经典测量方法。

交会定位的前提是必须至少两台设备同时捕捉到目标。以往测量初段就是从这时开始的，之前仅有一台设备的测量数据不能定位，这样就在目标运动起始到两台设备构成交会之间出现了一段轨迹空白。但这段轨迹结果又很重要，只好通过稍后形成交会的段落向前进行数值外推，来“推测”这一段的目标轨迹。由于运动初段目标的发动机刚刚启动，运动很不平稳，处于不断调整姿态的状态中，用外推方法给出的初段轨迹显然是不准确的，但以前也没有更好的办法。

在目标运动初段，各台经纬仪捕捉到目标往往有先有后，但只有两台或两台以上同时捕捉到目标，才能实现两台或多台交会定位，仅有一台拍到目标时无法形成交会。若不能定位，其数据白白浪费，而通常初段运动轨迹又非常重要，损失了十分可惜。

1.2 测距定位

测距定位虽然是一种单机定位方法，但必须得到测距信息，如经纬仪测角信息 （α、γ）并结合激光或红外测距信息R，才能实现单机定位。目标在测量坐标系下的坐标为：

（x，y，z）T＝ （Rcosαcosγ，Rsinγ，Rsinαcosγ）T

但以往这类经纬仪激光测距功能的实际应用并不成功，例如某型经纬仪加装激光测距仪，同时在目标上加装激光反射镜。然而，在多年应用的实践中，由于激光测距仪不能适应目标上激光反射镜的高速运动，无法接收到反射后的激光，导致测距成功率较低，大量测量数据中仅有测角信息而没有测距信息，使得激光测距经纬仪名不副实，仅能作为一般测角经纬仪来使用，无法实现单机定位。

2 近景单机定位

近景单机定位弥补了传统交会定位与测距定位的不足，首先不需要两台以上经纬仪，其次不需要实际工作中难以得到的测距信息，是一种易于实现的单机定位方法。

2.1 定位条件

近景单机定位时，目标不再被看作一个点目标，而且还要充分利用目标本身信息进行定位。在对高速运动目标的实际拍摄测量过程中，被摄目标常常处于近景中，这时所拍画面中目标细部特征较为清晰，利用这些信息可实现单机定位，进而延长目标的运动轨迹。所谓“近景”，以能否分辨画面中目标成像的特征点为判据。

和过去相比，现在拍摄的画面目标成像要比以前大，有的画面可以清晰分辨目标成像的特征点。而画面中目标成像的特征点能否分辨，除了与经纬仪镜头焦距有关以外，还与物距即经纬仪与目标距离有关。过去经纬仪布站较远，画面中目标成像较小，本方法自然不适用。但目前布站情况已有所改变，有的经纬仪距目标运动起始位置很近，拍摄的画面中成像目标较大，能够看清很多细部特征，可以设置多个特征点，找到很多有用的特征信息。利用目标上这些己知特征点信息，并考虑特征点的空间对应关系，通过计算确定特征点在测量坐标系中相对位置关系，可实现单经纬仪对目标的定位。

2.2 定位原理

在目标上预先标识一个三角形的三个顶点，则三角形的三条边长为已知量。用经纬仪近景拍摄运动中的目标，若在成像画面中三角形的三个顶点清晰可见，则可分别测得三个顶点的方位角、俯仰角，也为已知量。各顶点到经纬仪光学中心的距离（斜距）则为未知量，共三个。由未知的斜距与已知的方位角、俯仰角构成各顶点的极坐标，每个顶点在测量坐标系下的直角坐标可用极坐标来表示。为此，任意两个顶点间距离的平方即三角形边长的平方，就等于两顶点直角坐标分量差的平方和。这样由三角形的每条边可得到一个方程式，式中含有两个未知量和五个已知量，两个未知量为两顶点斜距，五个已知量为两顶点的方位角、俯仰角和该边边长。由三条边得到三个方程式，构成非线性方程组，对方程组求解，可得到三个未知量即三个顶点斜距，于是每个顶点的极坐标与直角坐标均被解出，完成了目标定位。

2.3 观测方程

假设目标上存在构成三角形顶点的3个特征点p1、p2、p3，其间距分别为p1p2＝r12、p2p3＝r23、p3p1＝r31。3个特征点p1、p2、p3在单台经纬仪的测量坐标系下极坐标为pi（αi，γi，Ri）（i＝1，2，3），其中αi、γi为特征点pi的方位角、俯仰角，为已知量；Ri（i＝1，2，3）为特征点pi至经纬仪光学中心距离（斜距），为未知量，记RT＝ ［R，R，R］T。设p在123i单台经纬仪的测量坐标系下直角坐标为pi（xi，yi，zi），（i＝1，2，3），如图1所示。则pi在测量坐标系中的直角坐标与极坐标关系为：

图1 三特征点目标定位原理Fig.1 Object positioning principle by 3feature points

而p1、p2、p3间距r12、r23、r31为已知常量，于是有：

将式（1）代入式（2），得：

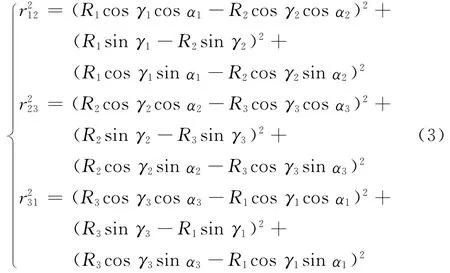
式（3）即为单经纬仪测量运动目标的观测方程，由此可解出未知量RT＝ ［R1，R2，R3］T。

2.4 方程求解

式（3）为非线性方程组，对此可采用Newtown迭代法求解，其计算步骤如下：

首先构造函数FT＝ ［f1，f2，f3］T，其中：

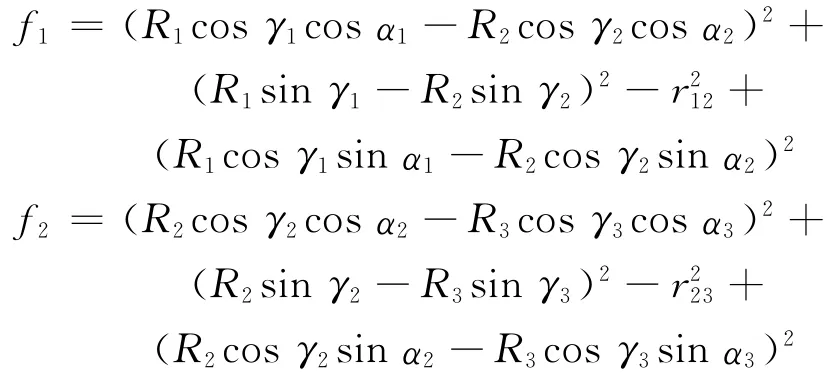
然后记J为FT关于RT＝ ［R1，R2，R3］T的Jacobian矩阵：

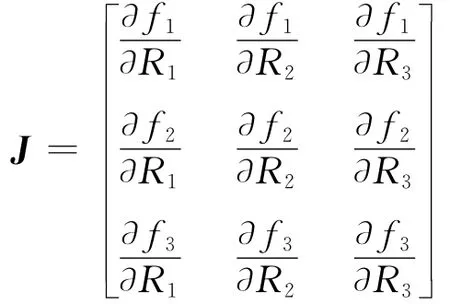
及J的逆矩阵J－1，则RT＝ ［R1，R2，R3］T的迭代公式为：

由式（4）得到方程的数值解RT之后，代入式（1），可求得本画幅中目标上特征点pi的测量坐标系下直角坐标（xi，yi，zi）T（i＝1，2，3），其中某一特征点pi的时间分布序列｛pi［j］｝（j＝1，2，…，N）即为pi点的运动轨迹。由于得到了本画幅中目标上多个特征点的坐标，甚至可以进一步计算目标的姿态。

2.5 特征点标识

在某些目标运动实况的拍摄过程中，可以得到运动目标近景图像，且画面中目标成像较大，可以事先在目标上标涂若干特征点标记，以便于测量判读。如对于柱形目标（单位为m），假定目标为长l，半径r的圆柱体，可在目标上设n圈，各圈间距d，每圈标涂6个十字特征点标记，相邻十字标记圆心角成60°，可保证视场内至少能看到两圈两列中三个特征点标记，如图2。于是相邻两圈同列特征点如A1B1间距d，同圈相邻特征点如A1A2间距r，邻圈邻列特征点如A2B1间距。

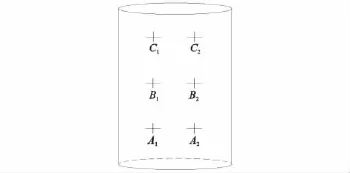
图2 目标中特征点标识Fig.2 Mark of feature point in object

若假设A1、A2、B1为p1、p2、p3，则r12＝r、r23＝、r31＝d。由经纬仪能够测量出此三个特征点的方位角、俯仰角信息，应用上述测量原理，可完成对运动目标的单机定位。

在目标运动初段时发动机刚启动，速度还不是很高。相对目标运动速度而言，经纬仪曝光时间极为短暂，因而每个画幅上目标的成像是非常清晰的，特征点的分辨不成问题。从动态测量时的实拍画面看，从来没有出现过因为目标运动速度过快，导致画面成像模糊的情况。目标在画面中的成像很清晰，目标上的字迹、线条等都可以看得很清楚，因此可以断定，如图2那样有选择地做一些标记点作为特征点，也应该同样看得清楚。

3 误差分析与仿真计算

3.1 误差分析

定位误差的误差源可视为由经纬仪的测角误差σαi、σγi（i＝1，2，3）与目标三角形边长的测量误差σr12、σr23、σr31构成，传递到测量坐标系。由观测方程（3）及坐标转换公式（1），可推得定位误差σxi、σyi、σzi（i＝1，2，3）的估算公式：

其中：

这里Kik、Li（i＝1，2，3；k＝1，2，…，9）为中间变量，Kik与αi、γi、Ri（i＝1，2，3）有关，Li则与αi、γi、Ri、r12、r23、r31及σr12、σr23、σr31、σRi、σαi、σγi（i＝1，2，3）有关，具体表达式略。

由上述公式，可以得出目标在测量坐标系下的定位误差σxi、σyi、σzi（i＝1，2，3）。

3.2 仿真算例

本文给出6个仿真算例。为简单起见坐标X轴指向目标三角形上部顶点投影方向，各例中目标距测站从约2 300m到近5 000m处。表1中给出各算例的已知数据和计算结果，其中三角形顶点测角信息为αi、γi（i＝1，2，3）、其间距为r12、r23、r31，所取迭代初值为，（其中可取，这些都为已知量。为考核算法的收敛性，初值选取故意与真值相距较远。从表1可知分别为47m、47m、74m、49m、127m、160m，但迭代的收敛速度还是很快的，6个算例的迭代次数均不超过10次。

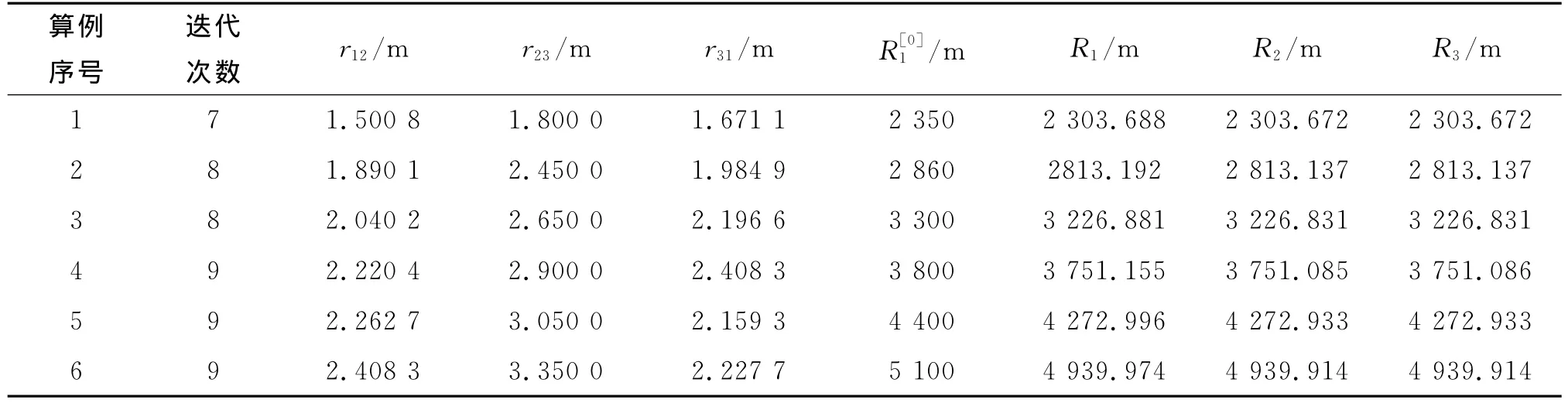
表1 仿真算例计算结果数据Tab.1 The calculating result data of simulation examples

算例中同时还以各目标三角形上部顶点为例，给出了单机定位的定位误差σx1、σy1、σz1的估算值（见表2），其中经纬仪测角误差值取σαi＝σγi＝20″（i＝1，2，3），σr12＝σr23＝σr31＝0.001m。从表2的结果数据可以看出，随着目标距离的增加，X方向的误差增加较快，Y方向与Z方向误差变化不大。

为与上述单机定位算例的定位误差比较，再增加一台经纬仪，与原经纬仪一起构成两台交会定位。两台经纬仪与被测目标构成直角三角形，原经纬仪与目标构成一个直角边，其长度与各算例中原经纬仪和目标的距离相一致；原经纬仪与新经纬仪构成另一直角边，其长度固定为3.0km不变；新经纬仪则与目标构成直角三角形的斜边。假定坐标系原点取原经纬仪光学中心，根据两台交会定位公式与误差估 算 公 式，算 得 两 台 交 会 定 位 误 差σ′x1、σ′y1、σ′z1。表2还给出了对6个目标三角形的上部顶点进行两台交会的定位误差。

表2 单机定位与两台交会的定位误差比较Tab.2 The comparison of position error of individual theodolite with twin intercross

与两台交会的定位误差相比，单机定位误差略大一些，但仍为同一数量级，因目标距离有限，误差总体上处于可接受的范围内。

4 结论

本文提出的单经纬仪定位方法，是在对运动目标进行近景拍摄的前提下，利用画面中目标较大可得到多个特征点，以及预知的特征点之间的位置关系的有利条件，根据经纬仪测得的角度信息完成目标定位。仿真算例表明：本文方法初值要求比较宽松，迭代收敛速度很快，说明本方法可行。从误差分析结果来看，误差可接受。

相对以往交会定位须有两台或两台以上经纬仪、单机定位必须增加测距信息情况，本文方法降低了定位条件，在仅有单台数据时增加了目标运动轨迹测量结果的长度，提高了有效样本量，这对众所关注的目标初段运动轨迹的描述，具有十分重要的意义。

［1］于晓峰.装备试验数据处理［M］.北京：国防工业出版社，2010.

［2］刘利生，吴斌，吴正容.外弹道测量精度分析与评定［M］.北京：国防工业出版社，2010.

［3］王敏，胡绍林，安振军.外弹道测量数据误差影响分析技术及应用［M］.北京：国防工业出版社，2008.

［4］刘利生，张玉祥，李杰.外弹道测量数据处理［M］.北京：国防工业出版社，2002.