调频引信模糊函数计算及调制参数提取方法

陈 思，赵惠昌，郭长勇

（南京理工大学电光学院，江苏 南京 210094）

0 引言

连续波线性调频引信是通过测量发射信号与目标回波信号的频率差值来提取目标与信源之间的距离信息的。由于它能解决距离分辨力和发射平均功率之间的矛盾，且其结构简单轻便、测距精度高、抗干扰能力强，在现代无线电引信中得到了广泛的应用［1－3］。研究如何在复杂的电磁环境中识别出连续波线性调频信号以及进行调制参数的准确提取是电子对抗的前提，具有重要的意义，国内外很多学者做了大量的工作［4－6］。但是，长期以来由于信号处理技术的限制，以及引信信号处理具有数据量大、实时性高的特点，使得线性调频引信的性能得不到充分的提升。文献［5］提出了利用分数阶傅里叶变换方法对线性调频无线电引信信号进行侦查，但文中没有分析噪声对侦查效果的影响。文献［6］给出了基于模糊函数的线性调频连续波（LFMCW）信号调制参数提取的理论和仿真分析，但其并没有分析此方法在实际应用中的可行性。

为此，本文提出了基于TMS320C6416DSP的引信信号模糊函数计算以及通过模糊函数提取其调制参数的方法。

1 连续波线性调频引信原理及其信号形式

1.1 连续波线性调频引信原理

连续波线性调频测距引信原理如图1所示［7－9］。线性调频调制器产生的调制信号调制射频振荡器产生的射频信号的频率，形成线性调频连续波，通过射频放大器放大后由发射天线辐射出去；回波信号经低噪放后与本地基准信号进行混频，得到差频信号。通过测量频率差值就能得到目标的距离信息。由于引信特殊的工作环境，使得其作用距离较近，处理和预警时间短，这就要求信号处理设备具有高的运算速度和强的处理能力。

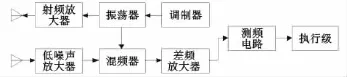
图1 连续波线性调频引信系统的基本原理框图Fig.1 Block diagram of LFMCW fuze system

1.2 锯齿波线性调频信号

连续波锯齿线性调频信号的表达式为：

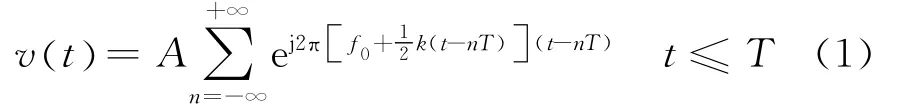
式中，A为发射信号的幅度，f0为信号的载波频率，ΔF为调制带宽，T为调制周期，k为信号的调制斜率，k＝ΔF／T。观察式（1）可知，需要提取的特征参数有ΔF、T和k。

1.3 锯齿波线性调频信号的模糊函数

在信号分析理论中，模糊函数是对引信信号进行分析研究和波形设计的有效工具，也是分析、比较信号处理系统优劣的重要手段。

信号的模糊函数的定义式为：

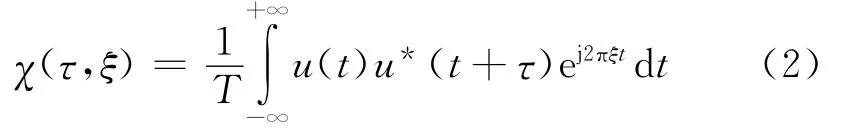
经推导［9］，锯齿波线性调频信号的模糊函数为：

它的周期模糊函数为：

图2为单周期（N ＝1）和二周期（N ＝2）LFMCW信号的归一化模糊图。从图中可以看出，其3D模糊图是由2 N－1个完整的“斜刀刃”和可以构成一个完整“斜刀刃”的两个半“斜刀刃”组成。它们之间相互平行，且峰值出现在调制周期整数倍上。观察图2（a）和（b）可知，信号的周期模糊图可以看成是单周期模糊图拼接而成，所以在后面分析中，只给出单周期的模糊图。

图2 线性调频连续波信号的模糊函数Fig.2 Ambiguity function graph of LFMCW signal

2 基于DSP的LFMCW信号的特征参数提取

基于DSP的锯齿LFMCW信号的参数提取程序流程框图如图3所示。其参数提取步骤如下：

步骤1：首先根据信号的时频特性对接收到的锯齿LFMCW引信信号进行n个周期提取，并将信号长度补零至2m点，以满足后续傅里叶变换（FFT）对信号长度的要求。

步骤2：其次将步骤1处理后的信号分为两路，一路直接进行FFT，另外一路乘以多普勒频移因子ej2πfdt后进行FFT。

步骤3：将上述两路变换后的信号相乘，并对相乘后的结果进行逆傅里叶变换（IFFT）。

步骤4：以上步骤即为对接收到的信号进行自相关变换。当多普勒频率fd在某频率范围内取不同值时，重复步骤2和步骤3，可得一个二维数组，此数组即为线性调频连续波信号的模糊函数。

步骤5：结合锯齿LFMCW信号本身的性质：其模糊函数的“斜刀刃”峰值出现在调制周期T的整数倍上；“斜刀刃”的斜率对应信号的调制斜率k；ΔF＝kT，可在相关域提取出锯齿LFMCW信号的调制参数。

图3 LFMCW特征参数提取的流程图Fig.3 The flow chart of parameters extraction of LFMCW signal

整个系统的硬件框图如图4所示。系统通过Xilinx公司生产的 Virtex－II Pro FPGA 产生两路正交的锯齿LFMCW信号，然后将数据打包，通过EMIFA总线将数据传送至DSP进行信号处理。由于需要处理的数据量大，需要使用片外的SDRAM做缓存。

在运算过程中，需要对每个频移都进行一次互相关，这就导致运算的数据量很大。本系统采用TI公司生产的TMS320C6416作为数字信号处理器。其时钟频率可达600MHz，最高处理能力为4800 MIPS（百万次指令每秒），每个时钟周期可以执行8条指令，且它提供了可同时操作的8个运算单元，能同时完成两个32bit数的乘法，这对于本系统中FFT／IFFT中的大量蝶形运算具有重要意义。本系统中FFT和IFFT的运算采用TI公司提供的库函数DSP＿fft32x32和DSP＿ifft32x32。

图4 系统的硬件结构图Fig.4 Hardware structure of the system

3 仿真计算及分析

3.1 锯齿波线性调频信号的产生

通过FPGA模拟产生一个LFMCW引信的目标回波信号，设信号的载波（即中频）频率f0＝15 MHz，调制带宽ΔF＝10MHz，调制周期T＝200 μs，采样频率fs＝50MHz。产生的信号如图5所示，该图放大至周期跳变点的位置，可以清楚地看到跳变点右边的信号频率为10MHz，左边的信号频率为20MHz。

图5 产生的LFMCW信号图Fig.5 The diagram of the LFMCW signal designed

3.2 锯齿波线性调频信号模糊函数的DSP实现

将上述产生的LFMCW信号通过数据总线传送给DSP，DSP接收到信号后，通过计算信号的时频特性求出信号频率跳变点的位置，从而提取出一个完整周期的信号补零至2m点后进行模糊函数的计算，计算的结果如图6所示。图6是没有加入噪声的模糊图。

图6 DSP计算的单周期的LFMCW模糊函数Fig.6 Single period ambiguity function graph of LFMCW signal calculated by DSP

根据1.3节所述，通过搜索2D模糊度图中频移的最大值和最小值，它们差值的一半即为信号的调制带宽10MHz。搜索3D模糊图，得到模糊函数极大值点对应的时延位置，相邻的时延位置的差值即为信号的调制周期，这里需要减去补零点产生的时延，最后得到的信号的调制周期200μs，与产生的信号的调制参数一致。

当信噪比SNR＝0dB时，信号的模糊函数图如图7所示。从图中可以看出，在SNR＝0dB时，仍然能清楚地体现出信号的特征参数。

3.3 参数提取与分析

根据上面介绍的识别LFMCW信号特征参数的方法，表1给出了在不同信噪比条件下单周期LFMCW引信信号的参数估计值。

图7 单周期的LFMCW模糊函数（SNR＝0dB）Fig.7 Single period ambiguity function graph of LFMCW signal calculated by DSP（SNR＝0dB）

表1 单周期LFMCW引信信号的调制参数估计Tab.1 Modulation parameter estimation of single period LFMCW fuze signal

从表1可以看出，利用模糊函数对LFMCW引信信号进行调制参数提取的抗噪声性能非常好。因为LFMCW引信信号在特定频移上的互相关函数集中分布，而高斯白噪声是没有这个规律的，高斯白噪声的模糊函数为“图钉形”的模糊函数，它并不能有效地干扰到通过模糊函数进行LFMCW引信信号特征参数的提取。另外，从表1、图6和图7中可以看出调制周期和调制斜率的提取稳定度比较高，在实际应用过程中，可以通过ΔF＝kT直接计算出调制带宽ΔF。

4 结论

本文阐述了一种基于高速定点DSP实现锯齿LFMCW引信信号特征参数提取方法。该方法首先在DSP中对截获或接收到的锯齿LFMCW引信信号进行周期提取并将信号的长度补零至2m点，然后对提取出的周期信号作二维自相关变换，最后结合锯齿LFMCW引信信号本身的特性，在相关域完成对LFMCW引信信号调制参数的提取。仿真实验结果表明：在不依赖于任何先验信息的条件下，该方法能够有效地提取出锯齿LFMCW引信信号的调制参数，且具有较强的抗噪声性能；完成的系统具有高的可靠性和实时性。

［1］Louis Brown.The proximity fuze［J］.IEEE A＆S Systems Mogtririon，1993，8（7）：3－10.

［2］Stove A G.Liner FMCW radar techniques［J］.IEEE Proceedings－F，1992，139（5）：343－350.

［3］Phillip E P.Detecting and classifying low probability of intercept radar［M］.Boston：Artech House Inc，2004：73－76；60－62.

［4］Ning Ma，Joo Thiam Goh.Ambiguity－function－based techniques to estimate DOA of broadband chirp signals［J］.IEEE transactions on signal processing，2006，54（5）：1826－1839.

［5］黄光明，赵慧昌，熊刚，等.基于分数阶傅里叶变换的无线电引信信号的侦查［J］.电子与信息学报，2005，27（3）：431－433.HUANG Guangming，ZHAO Huichang，XIONG Gang，et al.Radio fuze signal reconnaissance based on fractional fourier transform［J］.Journal of Electronics ＆Information Technology，2005，27（3）：431－433.

［6］刘静，赵惠昌，周新刚，等.基于模糊函数的无线电引信信号参数提取［J］.探测与控制学报，2009，31（5）：42－47.LIU Jing，ZHAO Huichang，ZHOU Xingang，et al.Parameter extraction of LFMCW fuze signal based on periodic ambiguity function［J］.Journal of Detection ＆ Control，2009，31（5）：42－47.

［7］林茂庸，柯有安.雷达信号理论［M］.北京：国防工业出版社，1984.

［8］郭磊，杨中海.LFMCW雷达信号多周期模糊函数分析［J］.电子科技大学学报，2004，32（3）：353－356.GUO Lei，YANG Zhonghai.Multi－period ambiguity function of LFMCW radar signal［J］.Journal of UEST of China，2004，32（3）：353－356.

［9］周新刚，赵惠昌，高振儒.LFMCW雷达信号多周期模糊函数分析再研究［J］.南京理工大学学报（自然科学版），2010，34（5）：624－627.ZHOU Xingang，ZHAO Huichang，GAO Zhenru.Comment on"Multi－period ambiguity function of LFMCW radar signal"［J］.Journal of Nanjing University of Science and Technology（Natural Science），2010，34（5）：624－627.