基于短波信道模型的天波雷达回波模拟方法

代 林，曾芳玲

（解放军电子工程学院，安徽 合肥 230037）

0 引言

电离层是一种随机、色散、不均匀和各向异性的传播媒质，会给利用电离层返回散射机理探测视距外目标的天波超视距雷达（SOTHR）造成巨大影响。例如，附加一个准随机扰动到回波信号的相位上，导致信号不能有效相干积累，杂波谱展宽。为准确描述电离层对回波信号的影响，采用或者建立合理的信道模型模拟天波雷达信号在电离层的传播是非常必要的。

当前，对于常规雷达回波信号建模［1］，国内外许多学者已经进行了广泛的研究，发表了大量的专著和文章。但常规雷达工作在微波频段，主要进行视距内的目标探测与识别，仅需考虑自由空间对电波的衰减和目标对发射信号的散射作用，回波信号的建模与仿真比较简单。文献［2］中阐述的天波雷达回波信号模型，仅考虑了天波传播过程中传播路径的增加，忽略了电离层的影响，不能完全反映出雷达信号传播过程中受到的影响。文献［3］在处理机动目标检测与跟踪问题时，仍然沿用了文献［2］中的回波模型，降低了仿真的难度，但也导致了获取距离参数的sinc状脉冲的位置发生偏移等问题。基于信号信道传输的思想，本文采用短波宽带信道模型——ITS模型来模拟天波雷达的回波信号。

1 ITS信道模型及简化模型

ITS模型［4－6］是一种适用于宽带和窄带两种情况的短波信道模型，能较为准确模拟电离层引起的多径效应、时延扩展、衰落、多普勒频移和频扩等影响。那么，对采用大时宽带宽积信号作为发射信号的天波雷达而言，可将信号在空中的传播分割为两个过程后分别利用ITS模型进行信号传播的模拟，从而得到天波雷达的回波信号模型。考虑到天波雷达探测目标的实际情况，对ITS模型进行相应的简化，使运用简化的模型进行回波模拟时，仍能有效地提取出回波信号的脉冲描述字（PDW）。

理想的ITS信道仿真模型的冲激响应h（t，τ）［4－6］是传播时间和传播时间延迟的函数，且由n路独立的传输模式冲激响应之和构成。

式（1）中，n表示传输模式。

1.1 功率延迟函数的近似

Pn（τ）为第n条模式的功率延迟函数分布函数，服从Gamma分布的形式，表示为：

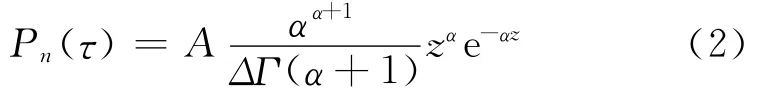
功率延迟函数是表示电波功率随延迟时间变化的关系式。对于确定目标的雷达回波来说，其延迟时间取决于目标与雷达的斜距及其径向速度。那么，采用斜距和径向速度表征确知目标时延函数的表达式［7］为：

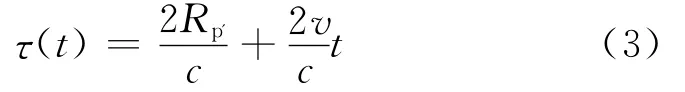
式（3）中，τ（t）为回波的时延函数，Rp＇为目标斜距，v为目标径向运动速度，c为光速。对于功率延迟函数，则

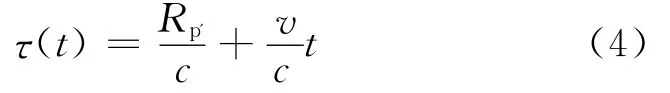
由于目标速度远小于光速，有限脉冲重复周期内返回接收天线的雷达回波的延迟函数趋近于一定值，故在雷达工作周期内，可用目标初始斜距引起的时间延迟代替回波随目标运动而引起的时间延迟。

采用球地面球面电离层模型［7］计算中远距离目标的斜距，即：

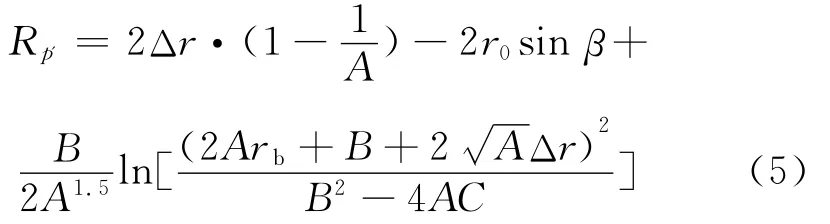
式（5）中，

r0为地球半径，rm为能反射入射波的最大电离层半径，ym为电离层半厚度，β为发射波仰角。

1.2 确定性相位函数的近似

Dn（t，τ）为第n条模式的确定性相位函数，表示为：

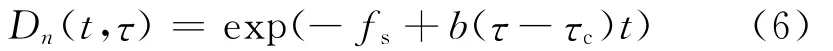
式（6）中，τ为传播时间延迟，fs为延时在τc处的多普勒频移，b为多普勒频移随延时的变化率。

文献［2］的实测数据如表1所示，可以发现由电离层介质造成的多普勒频移与距离无关，与信号极化方式无关，其值在零点附近变化，为了简化仿真，同时也为了模拟电离层对信号的确定性影响，可以在fs＝0.2，fsL＝0.1的条件下，模拟电离层对信号造成的多普勒频移。

表1 实测多普勒频域参数Tab.1 Measured Doppler parameters

1.3 随机调制函数的近似

ψn（t，τ）为随机调制函数，表征电离层附加到传播信号上的准随机扰动。它是一组关于时延相互独立，关于时间相关的随机序列，其自相关函数是信道的多普勒展宽。目前，有两种多普勒扩展形状：洛伦兹型和高斯型。从目前的研究情况来看，高斯型更适合Watterson模型，ITS模型采用洛伦兹型多普勒谱更符合实际情况。

目前，滤波法和莱斯正弦和法是产生色高斯随机过程的两种主要方法。滤波法可以产生特定的多普勒功率谱的随机过程，故本文采用此法。文献［2］提出了一种产生指数形式自相关随机序列的方法，如下式所示：

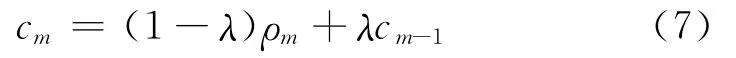
式（7）中，λ＝exp（－Δtσf），初始条件c－1＝0。ρm为实部和虚部相互独立且同分布的高斯随机序列，其均值为0，方差为1。该方法是将一复高斯序列ρm通过一个系统函数为H（z）＝（1－λ）／（1－λz－1）的单极点IIR滤波器，其极点为：

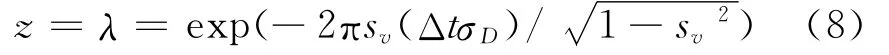
2 天波雷达回波模拟方法

天波雷达的信号在空中的传播可用信道的思想加以解释，电离层作为其传播的媒质，构成了影响其信道特性的主要因素。信号从发射天线到达目标的过程和由目标散射形成的散射波沿原路返回到达接收天线的过程可以视作两个相对独立的过程，分别加以考虑。

2.1 发射信号

为了克服高频雷达测速和测距精度较低，探测距离较近的缺点，天波雷达的发射信号采用大时宽带宽积信号，而线性调频连续波信号是其中运用较成熟的一种，表示为复指数形式：

式（9）中，f0为雷达载频，k＝B／T，为调制斜率。

当发射信号为单脉冲信号，即上式中M取值为1时，有：

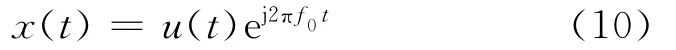
对u（t）进行傅里叶变换，再利用菲涅尔积分公式，可得其幅度谱为：

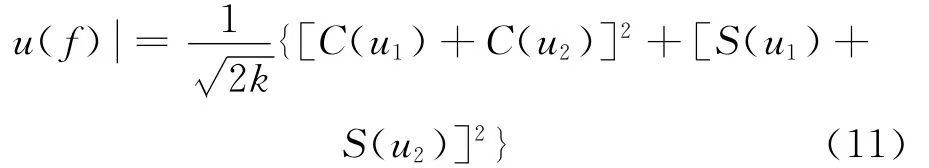
式（11）中，C（u）和S（u）由菲涅尔积分公式确定，

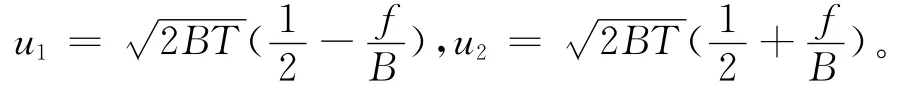
则单脉冲信号的振幅谱为：

当M大于1时，x（t）为多脉冲信号，其振幅谱为：

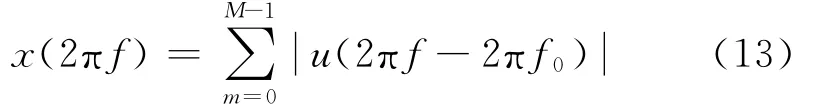
2.2 回波信号生成

采用ITS信道模型模拟无线电波在空中的传播过程如图1所示。那么，回波信号可以表示为：

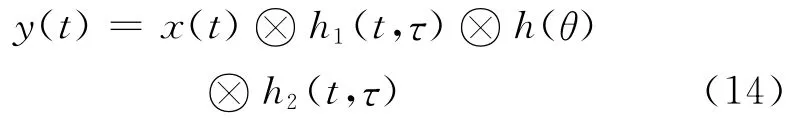
式（14）中，h1（t，τ）和h2（t，τ）表示基于ITS模型形成的信道冲击响应，h（θ）表示目标特性引起的冲击响应，反映散射信号的功率。

图1 传播过程图Fig.1 Transmission process

其频域响应为：

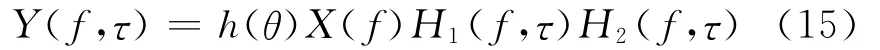
对式（15）进行傅里叶反变换可得雷达的回波信号。

2.3 路径传播衰减

电离层提供了天波雷达视距外探测的媒质，但它对电磁波的吸收和散射［7］也是引起回波功率下降的主要因素。以中纬度地区F层传播的天波雷达电波路径为例，其传播衰减可以表示为：

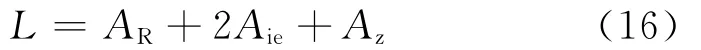
式（16）中，AR为自由空间扩散衰减，Aie为电离层衰减，Az为附加衰减，一般取为9.9dB。

电波自由空间衰减与常规雷达的衰减一致，本文重点讨论电离层衰减。电离层衰减包括电离层吸收衰减和Es层遮蔽衰减。

电离层吸收衰减分为偏移吸收和非偏移吸收，按垂直入射吸收测量数据可得其经验公式：

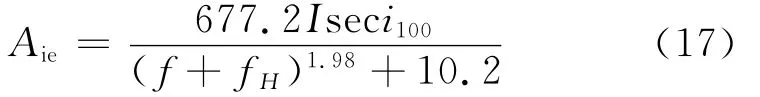
式（17）中，I为吸收指数，i100为射线入射角。

当存在Es层时，电波从Es层进入F层的过程中，其功率的一部分受到遮蔽，那么一次穿越的遮蔽衰减可以表示为：

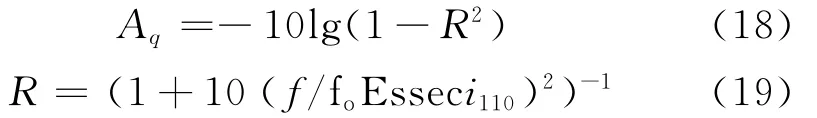
式（19）中，i110为高度110m处得射线入射角，foEs为Es层的临界频率。

3 仿真与结果分析

天波超视距雷达只能获得目标的方位和距离信息，通过回波脉冲时间延迟得到目标距离雷达的斜距，通过回波到达角判断目标所处的方位，由于电波在传播时会进入电离层，不是直接投射到目标上，不能获得目标的高度信息。本文采用对比回波信号与发射信号的幅度谱的方法验证仿真结果的正确性。

表2 距离参数表Tab.2 Distance parameters

根据赤道2 300km的天波信道实测参数，如表2和表3，对单模式天波雷达回波信号进行仿真。

表3 时延参数表Tab.3 Delay parameters

图2和图3分别对应单脉冲反射信号和多脉冲发射信号。单脉冲信号的脉冲宽度为10μs，其幅度谱以12.5MHz为中心，带宽为1MHz。多脉冲信号中，每个脉冲的宽度也是10μs，连续发射三个脉冲时宽度为30μs，其幅度谱仍以12.5MHz为中心，当其值更加集中。

图4对应单周期单脉冲的雷达回波信号，而图5对应单周期多脉冲的雷达回波。可以发现，由于路径噪声和电离层的影响，可从回波信号的时域波形中看到明显的脉冲痕迹，而其幅度谱与发射信号的幅度谱基本相同，其值有很大程度的减小，带宽基本保持一致。

图2 单脉冲发射信号及其频谱Fig.2 Single pulse LFM and the spectrum

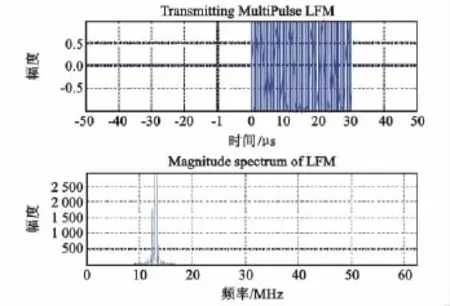
图3 多脉冲发射信号及其频谱Fig.3 Multi－pulse LFM and spectrum

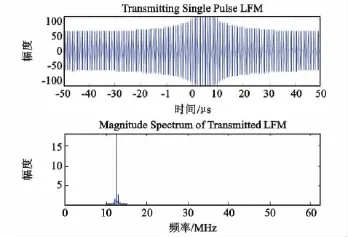
图4 单脉冲雷达回波信号及其频谱Fig.4 Single pulse LFM echo and the spectrum

图5 多脉冲雷达回波及其频谱Fig.5 Multi－pulse LFM echo and the spectrum

4 结论

本文提出了采用ITS模型来模拟天波超视距雷达的回波信号。此法在考虑雷达回波模拟时对回波信号自身携带的信息要求较低的情况下，通过对实测信道数据分析，利用简化的ITS模型分阶段表示电波在空中的传播过程，从而得到天波雷达的回波信号。仿真实验表明：与发射信号相比，仿真形成的回波信号引入较明显的外部噪声后，通过对比时域波形仍能大致得到回波的波形；而据回波信号在频域形成的谱峰则更易判别目标位置。对由电离层影响导致的天波雷达回波信号的确定性相移和准随机相位扰动的模拟，也能通过多次重复仿真得到验证。但由于ITS模型在处理目标高速运动方面的局限性，本文仿真的回波未对高速运动目标的多普勒特性进行详细分析，这将是下一步工作的重点。

［1］刘洋，朱立东.一种改进的窄带短波信道模型及仿真实现方法［J］.通信技术，2009，42（5）：1－4.LIU Yang，ZHU Lidong.An improved narrow band high frequency channel model and simulation algorithm［J］.communication Technology，2009，42（5）：1－4.

［2］陈强.天波超视距雷达系统仿真［D］.南京：南京理工大学，2006.

［3］殷俊丽.天波超视距雷达机动目标检测与跟踪［D］.西安：西安电子科技大学，2009（1）：26－28.

［4］Vogler L E，J A Hoffmeyer.A new approach to HF channel modeling and simulation－part I：deterministic model［R］.US：NTIA Report，1988.

［5］Vogler L E，J A Hoffmeyer.A new approach to HF channel modeling and simulation－part II：Stochastic Model［R］.US：NTIA Report，1990.

［6］Vogler L E，J A Hoffmeyer.A new approach to HF channel modeling and simulation－part III：Transfer Function［R］.US：NTIA Report，1992.

［7］朱今祥.电离层探测系统的仿真研究［D］.青岛：中国海洋大学，2005.