考虑扭转力矩的塑料贮液瓶薄弱环节设计方法
李世文,王莹澈,李仁杰,贺 文
(西安机电信息技术研究所,陕西 西安 710065)
0 引言
铅酸储备电池贮液瓶一般采用玻璃、金属、塑料等材料。玻璃瓶长期储存性能好,但破瓶加速度散布大,安全与可靠激活矛盾尖锐,特别是在注入电解液后融封过程中内部产生应力不易消除,易在温度剧变时自爆;金属瓶破瓶力散布小,但工艺复杂,成本高。针对小口径火炮引信,玻璃瓶与金属瓶的共同缺点是尺寸较大,如果缩小尺寸,玻璃瓶破瓶可靠性下降,金属瓶破瓶难度大,成本更高。塑料贮液瓶采用聚乙烯材料塑压成型,强度好,工艺简单,具有一定的抗渗漏性,尤其能满足小口径火炮引信的尺寸要求。
塑料贮液瓶在瓶体切割加工出薄弱环节,人为制造应力集中部位,使得加重块在发射后坐过载下拉断薄弱环节,从而激活电池。目前的塑料贮液瓶薄弱环节设计只考虑发射后坐过载,对于旋转弹并不适用,弹丸加速转动过程中角加速度造成的扭转力矩对薄弱环节的断裂有着重要影响,为此本文提出了一种考虑扭转力矩的薄弱环节尺寸设计方法。
1 塑料贮液瓶薄弱环节
1.1 塑料贮液瓶结构
铅酸储备电池主要由电极组件、贮液瓶、固定装置组成。贮液瓶固定在电极组件形成的圆形空间内,激活后,电解液从贮液瓶流出,在离心力的作用下持续进入电极反应区,发生化学反应产生电流。
塑料贮液瓶由塑压部件、加重块和电解液组成,薄弱环节位于塑压部件中部。典型的塑料贮液瓶结构如图1所示。

图1 典型的塑料贮液瓶结构Fig.1 Typical construction of plastic liquid storing bottle
薄弱环节尺寸由外径尺寸R1和内径尺寸R0决定。贮液瓶薄弱环节是人为制造应力集中部位,以保证发射过载下贮液瓶能可靠破瓶,因此只要连接可靠,贮液瓶的裂纹产生和断裂扩展都应该是在薄弱环节处。
1.2 薄弱环节处的变形理论
发射环境下,贮液瓶受发射直线惯性力和离心力的作用,电解液因后坐产生了对贮液瓶的压力,此时,薄弱环节处同时受拉力、剪切力和压力的作用,采用第四强度理论进行计算。
根据第四强度理论[1],材料超过屈服极限的条件为:
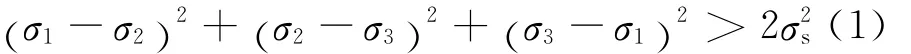
跌落状态下,贮液瓶只受惯性力的作用。对薄弱环节产生最大惯性力的方向为平面着地方向,若该方向跌落安全无损,便能保证电池在勤务处理中的安全性。

1.3 目前的薄弱环节尺寸设计方法
薄弱环节的内径尺寸R0一般由电池整体尺寸和电解液量决定,现主要讨论外径尺寸R1。现已知R0数值、发射过载直线加速度极值a1、跌落状态下直线加速度极值a2、贮液瓶总重量M,塑压部件材料抗拉压强度σs。令A0为薄弱环节处的面积,其值为:
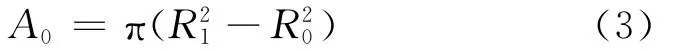
发射状态下的校核为:
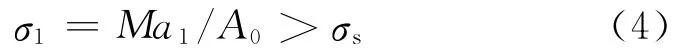
跌落状态下的校核为

令发射状态安全系数为n1,则有

令跌落状态安全系数为n2,则有

通过比较方法,当安全系数n1=n2时,可以获得最后的R1尺寸。可以看出,目前的薄弱环节尺寸设计方法只考虑后坐直线惯性力,没有考虑弹丸加速转动过程中角加速度造成的扭转力矩。
2 薄弱环节尺寸设计方法
弹丸发射状态下角加速度造成的扭转力矩对薄弱环节的断裂有着重要影响,尺寸设计中必须考虑该因素。通过逐步缩小薄弱环节尺寸可行区间,最终获得的最优尺寸可同时保证跌落无损。
2.1 薄弱环节处的力学分析
已知薄弱环节处的面积A0表达式为式(3)。
F1是跌落、锤击或发射时受的惯性力,方向是向下。其值为

式(8)中,M =m1+m2+m3;m1为加重块重量,kg;m2为电解液的重量,kg;m3为贮液瓶塑压部件薄弱环节以下部分的重量,kg;G1为贮液瓶受到的直线加速度,m/s2,取跌落、锤击或发射时过载的峰值进行计算。
F2是重力,方向向下。其值为:

式(9)中,G2:重力加速度,取10m/s2。
T是发射环境下薄弱环节以下部位对薄弱环节的扭转力矩。其值可近似为:

F3是发射环境下电解液对瓶体的单向压力。其值较小,相比于发射直线惯性力可忽略不计。
整个过程中合力的表达式如下:
拉伸力

扭转力矩
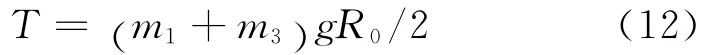
根据第四强度理论,则有
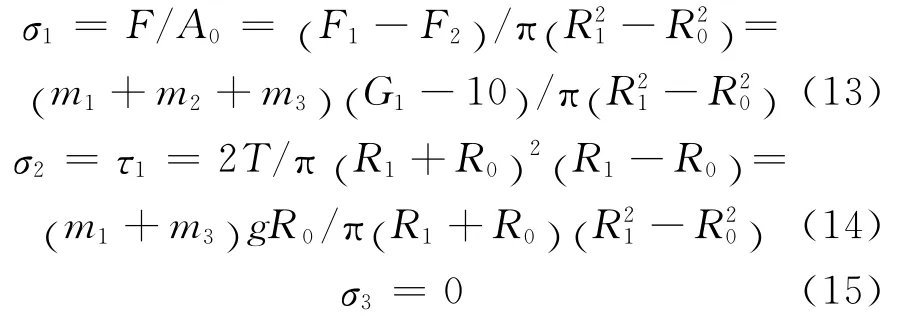
2.2 薄弱环节处尺寸取值方法
发射状态的条件可以确定一个薄弱环节尺寸最大值,跌落状态的条件可以确定一个薄弱环节尺寸最小值,二者之间可建立一个尺寸关联公式,逐步缩小可行区间,最终可确定薄弱环节尺寸的一个最优值。令安全系数n
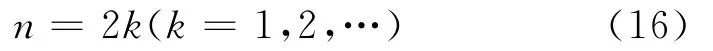
则有薄弱环节处的关联公式

3 仿真验证
3.1 计算实例
3.1.1 设计参数
加重块重量m1为1.06×10-3kg;电解液的重量m2为8.22×10-5kg;贮液瓶薄弱环节以下部分重量m3为5.05×10-5kg;某旋转弹发射情况下时G1为40 000 g,即392 000m/s2;1.5m跌落状态下G1为7 500m/s2;贮液瓶内径尺寸R0为3.25×10-3m;贮液瓶材料为高密度聚乙烯树脂(HDPE),抗拉压强度σs为22MPa。
3.1.2 计算结果
将上述数据代入关联公式(17),当k=2时即安全系数n=4时,经计算得出3.3mm<R1<3.5 mm,因此取R1基本尺寸为3.4mm,加工精度为C13,本研究最终取R1值为(3.4±0.07)mm。
3.2 ANSYS仿真分析
利用ANSYS软件对贮液瓶进行可靠激活分析和安全跌落分析。该型贮液瓶为轴对称结构,因此为了简化仿真过程中的计算量,在不影响结果正确性和真实性的前提下,定义贮液瓶模型的材料属性[2],选用贮液瓶模型1/4进行建模,有限元网格划分后的贮液瓶有限元模型如图2所示。
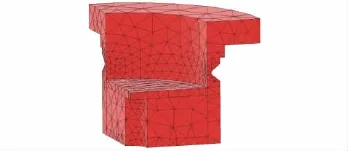
图2 塑料贮液瓶有限元模型Fig.2 Finite element model of plastic liquid storing bottle
3.2.1 可靠激活分析
输入的仿真数据如图3所示,内弹道发射过载简化为周期为300μs的三角波,峰值为392 000 m/s2,后面500μs为自由振动时间,将该数据输入ANSYS软件中,进行动力学仿真[3]。仿真结束后输出贮液瓶的应力云图和薄弱环节处的位移情况[4-5]。

图3 内弹道发射过载简化示意图Fig.3 Simplified diagram of internal trajectory recoil overload
由图4和图5可以看出,在受到40 000 g的发射过载作用时,薄弱环节处位移大,所受的应力极值为231MPa,整个环槽应力最低值也达到了120 MPa,远远大于HDPE的抗拉压强度22MPa,且整个环槽受力比较均匀,薄弱环节很可能整体断裂,这说明贮液瓶在发射过载作用下能可靠激活。

图4 塑料贮液瓶应力云图Fig.4 Equivalent von-stress of plastic liquid storing bottle

图5 薄弱环节处位移-时间曲线Fig.5 Displacement-time curve of weak link
3.2.2 安全跌落分析
1.5 m安全跌落试验的过载数据近似看作幅值7 500 g、周期为110μs的三角波,如图6所示,后续时间为自由振动时间,进行动力学仿真。
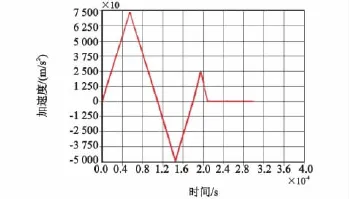
图6 1.5m跌落状态下过载示意图Fig.6 Simplified diagram of fall off 1.5moverload
图7和图8显示了在1.5m跌落状态下贮液瓶各部位尤其是薄弱环节所受的应力情况和形变情况,由图可知1.5m跌落状态下薄弱环节处位移极小,受到的最大应力值为14.6MPa,远小于HDPE的抗拉压强度22MPa,这说明1.5m跌落试验不会造成贮液瓶破裂,可以做到跌落无损。

图7 塑料贮液瓶应力云Fig.7 Equivalent von-stress of plastic liquid storing bottle
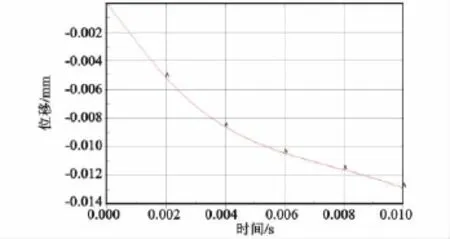
图8 薄弱环节处位移-时间曲线Fig.8 Displacement-time curve of weak link
4 结论
本文提出了一种考虑扭转力矩的薄弱环节尺寸设计方法。该方法将弹丸加速转动过程中角加速度造成的扭转力矩加入计算,利用发射过载-扭转力矩和跌落过载确定薄弱环节尺寸可行区间,通过调整安全系数逐步缩小尺寸可行区间获得尺寸最优值。仿真表明:通过该方法获得的薄弱环节尺寸可以提高安全系数,有效保证可靠激活和跌落无损,为旋转弹引信用铅酸储备电池塑料贮液瓶薄弱环节尺寸设计提供了思路。不足之处是本文的计算只是粗略估算,且没有考虑薄弱环节性能受加工工艺的影响变化,还需要做进一步研究。
[1]苟文选.材料力学[M].北京:科学出版社,2005.
[2]《塑料工程手册》编委会.塑料工程手册[M].北京:机械工业出版社,2000.
[3]郝好山.ANSYS12.0LS-DYNA 非线性有限元分析从入门到精髓[M].北京:机械工业出版社,2010.
[4]王佳伟,霍鹏飞,陈超.基于蒙特-卡洛法的冲推器数量与冲量优化[J].探测与控制学报,2010,32(1):92-95.WANG Jiawei,HUO Pengfei,CHEN Chao.Number and impulse optimization of lateral pulse jets based on Montecarlo method[J].Journal of Detection & Control,2010,32(1):92-95.
[5]徐蓬朝,黄惠东,揭涛,刘璞.高超音速侵彻引信中的泡沫铝垫片[J].探测与控制学报,2010,32(6):63-68.XU Pengzhao,HUANG Huidong,JIE Tao,LIU Pu.The foamed aluminium gasket in hypersonic penetrating fuze[J].Journal of Detection & Control,2010,32(6):63-68.

