基于协变光谱随机场理论的激光引信背景模型

田 博，于 宇，李 伟，李 鹏

（1.机电动态控制重点实验室，陕西 西安 710065；2.西安机电信息技术研究所，陕西 西安 710065）

0 引言

随着世界范围内局部军事冲突的日益加剧，各国在激光近炸武器研制领域研究不断加大投入，我国在20世纪60年代已开展了激光近炸引信研制并在此之后不断加快研制步伐。新的激光近炸引信的研制对激光引信的仿真提出了更高要求——仿真效率更高、仿真精度更高。在激光引信作用过程中，背景的随机性、复杂性使得背景模型成为制约系统仿真精度和效率的瓶颈，如何建立更高效、更精确的背景模型已成为激光引信仿真系统的关键问题，激光背景杂波模型的准确性关系到系统的整体仿真精度和可靠性，对其有着迫切的需求。

背景杂波从本质上讲是电磁波或光波照射到不确定的物体或背景上因散射而产生的杂散回波。这些物体或背景往往是不规则的客体，因此所产生的杂波也是不确定的。传统的杂波分析方法是从幅度分布和谱分布等方面入手，把杂波建成一种随机过程模型，如最初的正态分布以及后来的对数正态分布、Weibull分布，Rayleigh分布和 K分布等［1］。传统方法生成的海杂波模型方程求解困难，实时计算效率较低，且未考虑到引信使用中的系统分布及控制参数，不能满足激光引信仿真对实时性、真实性的要求。针对上述问题，本文提出了基于协变光谱随机场理论的地海杂波背景模型。

1 传统杂波随机场理论

由于海浪变化的随机性、不确定性，传统杂波随机场理论通常把海浪看作是一种具有各态历经性的平稳正态随机过程，属于线性海浪理论的范畴。对于海浪模型的研究，一般利用海浪的频谱方法，通过随机过程理论分析给出各种情况下海浪运动的统计特性。

目前，地海杂波模型方面研究较多的是海杂波电磁散射模型。Ward提出了复合K分布海杂波，它不仅能够很好地拟合海杂波的幅度，还便于描述海杂波的时间和空间相关性；Berizzi［2］等建立了一维和二维海面分形模型，并且发展了海杂波分形仿真和目标检测方法；吴振森、郭立新等研究了分形粗糙面的电磁散射，并给出了散射场的分形规律［3］。在光波段海杂波模型研究方面，Fournier采用参数曲面来模拟波峰卷曲的波浪，但不能对几组波进行叠加；Foster［4］采用数值迭代方法求解二维的Navier－Stokes方程，即利用经典流体力学来建立水波模型；史春波提出基于PM海浪谱的随机海浪模型［5］，并利用线性叠加法进行了海浪的仿真。

上述传统随机场理论在生成海杂波时，都是生成服从一定概率分布的海杂波，前提是事先知道海杂波的功率谱密度，且这种方法只适用于对静态观测时的海杂波进行建模。如海杂波线性理论模型中，海浪可看作一个随机过程，是由无限个随机的余弦波叠加而成的：

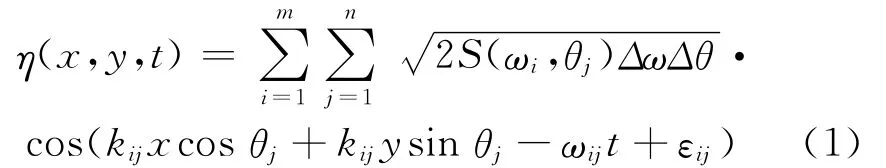
式（1）中，η（x，y，t）是海洋表面在t时刻的瞬时幅度函数；S（ωi，θj）为海浪方向谱；Δω为频率计算步长，其划分一般采用频率等分法或者能量等分法；Δθ为方向计算步长，采用等分法获取；kij为谐波数；εij为在0～2π范围内服从均匀分布的随机初相位；ωij为波频。

而在实际情况下，海杂波的功率谱密度是未知的，采用K分布、对数正态分布、Weibull分布，Rayleigh分布等这些常见分布形式的地海杂波模型与实际功率谱差异较大且适用范围受到限制，如大入射角、特定海情等限定条件。传统随机场模型的上述局限无法满足现代激光引信仿真计算结果真实性、仿真环境复杂性的要求。

2 基于协变光谱随机场理论的激光引信背景模型

基于协变光谱随机场理论的激光引信背景模型将均匀各相同性随机场非典型光谱模型与协变函数函数及多维分布定律合成，将背景的不可预期分布用非典型光谱随机亮度分布场来模拟。与传统随机场理论有所区别的是，随机场分布函数不是采用目前常见的分布形式，而是根据大量实测背景模型数据统计特征，使用计算机将光电雷达（引信探测、信号处理系统）的背景干扰［6］信号响应作用以协变函数及分布定律来描述、约束随机场分布从而复现出真实信号。综上，建立基于协变光谱随机场理论的激光引信背景模型分为三步：首先找到具有真实背景场统计特征的协变函数；其次结合光谱理论将随机场亮度分布求解转化为随机频率、功率谱及概率密度求解，以避免求解大量复杂方程提高计算效率；最后融合上述两步模型数据，形成最终模型。这种模型不但可描述海面背景，通过协变函数的变化还可以描述诸如草原、沼泽、灌木丛、雪地等背景，在激光武器仿真中可以很方便地模拟各种背景情况，具有较好的适应性。相比目前常见的各种杂波背景模型，解决了模型用途单一、方程求解困难、不适应激光引信系统仿真应用的问题。

2.1 具有真实背景场统计特征的协变函数

将具有零数学期望值和单位离散差的多维均匀随机场非典型光谱参数模型ε（x1，…，xN）表示为独立谐波统计总合的形式：

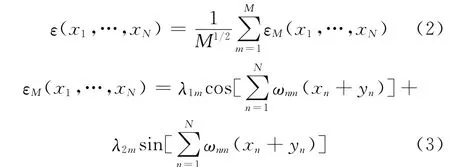
式（3）中，λ1m，λ2m为零数学期望和单位离散差的独立随机量；｛ω11，…ωn1｝，…，｛ω1M，…ωNM｝为 M 个随机矢量｛ω1，…ωN｝的独立实现值。

不难看出，公式（3）描述的随机场是均匀的，具有零数学期望值和数值为1的单位离散差，且它的光谱密度与随机量｛ω1，…ωN｝的 N 维概率密度WN（V1，…，VN）相一致。换句话说，公式（2）描述的协变函数与随机量λ1m、λ2m的分布形式无关。

为使上述均匀随机场能够代表某种背景场，通过对大量真实背景场的实测数据进行统计分析，找出合适的协变函数结构来约束随机量｛ω1，…ωN｝的分布规律。经过实测数据统计获得的协变函数约束后，背景亮度随机场的分布具有了该种背景的统计分布规律。这种基于协变函数的背景亮度随机场概率密度函数可以表示为：

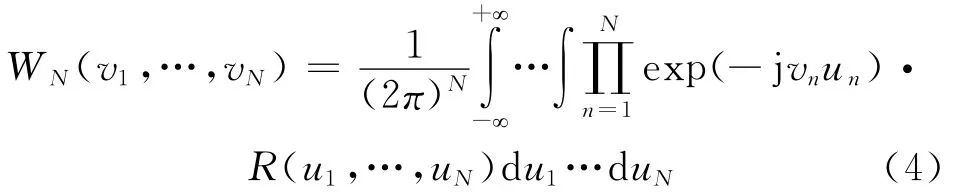
2.2 结合光谱理论的背景亮度随机场近似计算方法

使用基于协变函数的背景亮度随机场概率密度函数方法描述某背景时，可将求解均匀各向同性场光谱模型随机频率ωN的问题转化为计算RN的概率方向和概率密度的随机量。

对于大多数振荡协变函数来说，上述概率密度函数很难进行有限积分。因此，需要结合光谱理论对实际应用的频率矢量模分布规律进行近似计算。

当随机场的协变函数在衰减区间内有4个以上极值时可以把概率密度W1（v）对N维矢量模分布的导数分解成级数形式。当协变函数在衰减区间内有3～4个极值的情况下可以用协变函数最小近似误差标准来优化。在协变函数极值为1～2个时则采用矢矩法进行求解。

在概率密度为W1（v）的光谱场频率矢量计算时，N维矢量模展开并求积分后得到：

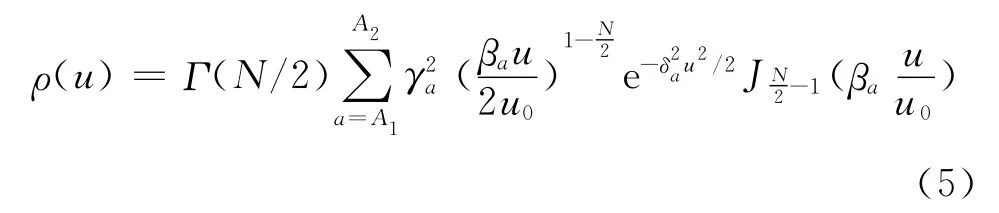
式（5）中，βa为函数（t）的根级数；u0为函数ρ（u）的衰减半径。

上述级数公式能很好地描述协变函数。利用此公式按照场协变函数近似计算的最小误差标准计算求出参δa，γa的值。计算表明A1值最好选择等于协变函数的极值数量，这时分解两项就可以精确地计算出协变函数的近似值。

2.3 基于协变函数、光谱理论的激光引信背景随机场模型

为了仿真计算方便，假设上述公式（2）中的光谱场模型独立随机振幅λ1m，λ2m（m ＝1，2，…，M）是均匀分布的。此时按中心边界定理在M增大时随机场的分布趋向于法向分布，偏移的大小等于该分布的累积系数，其中也包括非对称系数及过度量。无法使用改变随机振幅概率密度的办法来得到随机场的高斯均匀分布。

为得到带有均匀分布函数和协变函数的非高斯均匀各向同性场可以利用高斯场的非线性无惯性变换得到。在对非高斯均匀各向同性场η（x1，…，xN）变换时，高斯场分布随着协变函数（u）的变化而变。其变化关系可用下述累积方程表示：

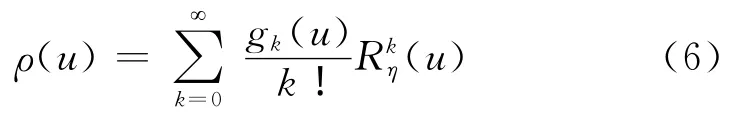
由此可知，在相关理论范围内随机场非线性无惯性变换问题核心在于求出函数gk（u）。此函数可以非线性随着随机场分布η（x1，…，xN）的全部累积量的变化而改变。为了提高仿真计算速度，对函数gk（u）进行了近似计算从而快速得到非高斯均匀各向同性场η（x1，…，xN）。

3 模型验证分析

通过大量的自然界背景外场实测试验表明，均匀各向同性随机场接近于法向分布及振荡协变函数，并且在初始区间上有较快的衰减速度。这种随机场是诸如草原、沼泽、灌木丛、海水、雪地等背景类型光学亮度场的最佳统计模型。

以雪地背景为例，图1是雪地实测亮度场相关系数与模型计算的协变函数相关系数对比曲线。由图中可以看出实测背景亮度场相关系数与仿真模型计算协变函数相关系数曲线统计均方差（RMS Error）为10.4%，根据此组协变函数相关系数可用基于协变光谱随机场理论的激光引信背景模型合成上述背景随机场的概率密度函数及随机概率函数。最终使用不同数量的空间谐波实现基于协变光谱随机场理论的背景亮度分布图（图2）及频率概率密度曲线（图3）。

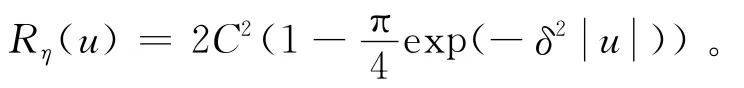
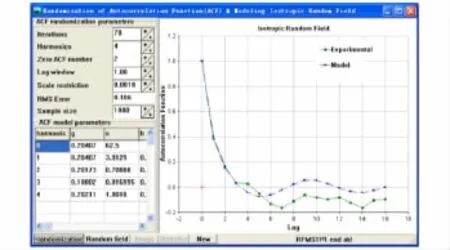
图1 雪地背景实测与仿真协变函数曲线Fig.1 The form for snow－covered field background model

图2 雪地背景仿真图像Fig.2 Simulation image of snow－covered field background model

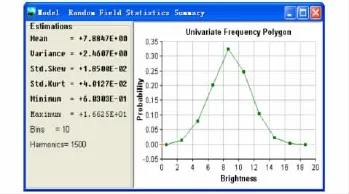
图3 雪地背景频率概率密度统计特征图Fig.3 Sample statistics of snow－covered field background model

由雪地背景、微浪海面背景及其它一些地海背景的仿真计算可以看出，基于协变光谱随机场理论的激光引信背景模型仿真结果统计均方误差（RMS Error）不大于20%，具有较好的精度。

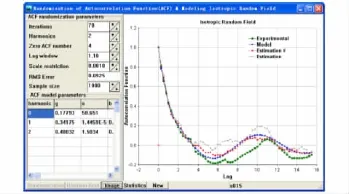
图4 微浪海面实测与仿真协变函数曲线Fig.4 The form for surf background model

图5 微浪海面亮度仿真图像Fig.5 Simulation image of surf background model

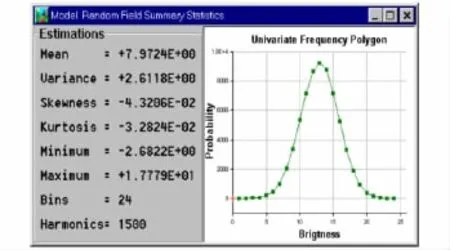
图6 微浪海面频率概率密度统计特征图Fig.6 Sample statistics of surf background model

4 结论

本文针对传统地海杂波随机场模型进行改进，提出了基于协变光谱随机场理论的激光引信背景模型。该模型首先找到具有真实背景场统计特征的协变函数，再结合光谱理论将随机场亮度分布求解转化为随机频率、功率谱及概率密度求解，最后融合上述理论得到背景模型。经实际测试验模表明：实测结果与仿真结果误差小于20%，模型可用于各种激光近炸引信仿真中。需要注意的是，约束模型的协变函数是通过对实测数据统计获取的，对一类背景建模时必须获取一定样本量的实测数据对模型进行训练优化才能得到最佳的协变函数。因此，仿真前必须获取足够的测试数据保证模型计算精度。

［1］Farina A，Gini F，Greco M V.Analysis of sea clutter radar data Radar［J］.Proceedings of the CIE International Conference of Radar，1996（10）：115－118.

［2］Berizzi F，Dalle－Mese E.Scattering from a 2－D Sea Fractal Surface：Fractal Analysis of the Scattered Signal［J］.IEEE Trans on A＆P（S0018－926X），2002，50（7）：912－925.

［3］王运华，郭立新，吴振森.改进的二维分形模型在海面电磁散射中的应用［J］.物理学报，2006，55（10）：214－222.WANG Yunhua，GUO Lixin，WU Zhensen.The application of an improved 2Dfractal model for electromagnetic scattering from the sea surface［J］.ACTA Physica Sinica，2006，55（10）：214－222.

［4］Foster N，Metaxas D.Modeling water for computer animation［J］.Communications of the ACM（S0001－0782），2000，43（7）：60－67.

［5］史春波，苏建忠，马献华.激光引信飞行仿真中的随机海浪模型［J］.探测与控制学报，2009，31（3）：5－8.SHI Chunbo，SU Jianzhong，MA Xianhu.Random wave model establishment for laser fuze flying simulation［J］.Journal of Detection ＆ Control，2009，31（3）：5－8.

［6］王广生.激光引信抗超低空地杂波干扰技术研究［J］.探测与控制学报.2004，26（1）：13－17.WANG Guangsheng.Study on anti－ground－clutter techniques for laser fuze at extreme low－altitude［J］.Journal of Detection ＆ Control，2004，26（1）：13－17.