高速微注射成型中熔体充填模式及裹气机理研究
张世勋,曹 伟,叶曙兵,李 倩,申长雨
(1.郑州大学橡塑模具国家工程研究中心,河南 郑州450002;2.深圳市兆威机电有限公司,广东 深圳518103)
高速微注射成型中熔体充填模式及裹气机理研究
张世勋1,曹 伟1,叶曙兵2,李 倩1,申长雨1
(1.郑州大学橡塑模具国家工程研究中心,河南 郑州450002;2.深圳市兆威机电有限公司,广东 深圳518103)
为了准确模拟聚合物熔体在型腔中的流动及前沿位置和形态,建立了熔体、气体两相流流动模型,构造了熔体流动的黏弹性本构关系,并采用水平集方法预测和跟踪熔体流动前沿,模拟了熔体在低速、中速、高速条件下的流动状态和充填模式,分析了高速微注射成型中气孔产生的原因和可能出现的位置,开展了实际产品的高速微注射成型实验,比较了模拟结果和实验结果。研究表明,熔体充填模式与注射速度、材料特性、型腔尺寸密切相关,在喷射充填模式下可能产生裹气。
微注射成型;两相流;充填模式;黏弹性模型
0 前言
与常规注射成型相比,高速微注射成型数值模拟需要考虑尺寸效应及气体聚积现象。Yao等[1]建立了微流动的微观黏度模型,并在常规Hele-Shaw流动模型中加入了滑移边界和表面张力等边界条件,发现边界滑移效应随尺寸的减小而增大,而表面张力效应随注射压力的增大而显著减小,Kim等[2]用三维数值模拟也发现了类似的规律。最近,Choi等[3]提出了模拟带有微特征制品成型的多尺度方法,而且发现当微特征的尺寸小于10μm时需要加入滑移边界条件。随着注射速度的增加,型腔中聚积的气体会对熔体的充填产生阻碍作用,并对多型腔流动平衡产生影响,曹伟等[4]和Griffiths等[5]分别用数值模拟和实验方法研究了气体的聚积及其对熔体充填及流动平衡的影响。
虽然学术界在滑移边界、表面张力及微观黏度等尺寸效应研究上取得了重要进展,但屹今为止尚未出现高速注射成型中有关流体充填模式的报道,也未发现熔体裹气现象及机理等相关研究,而深圳兆威机电有限公司在实际生产中发现当以800mm/s的注射速度成型带有微特征的斜齿轮时,熔体在较大型腔内产生了喷射,并在壁厚方向形成了气孔。由此可见,在高速微注射成型中,熔体不完全按照传统的近至远顺序充填模式充满整个型腔,可能在较大空腔处产生喷射,并可能与后期到达的熔体形成裹气。因此,探索高速注射成型熔体的充填模式及裹气机理对微注射成型模拟及制品质量预测是十分必要的。
本研究借鉴金属压铸成型中两相流模拟裹气原理[6-7]建立耦合的熔体流动、气体流动模型,用数值模拟方法探索高速微注射成型熔体的充填模式,研究熔体裹气产生的力学机理,分析影响熔体充填模式的主要影响因素。开展实际制品的微注射成型实验,比较模拟结果与实验结果,分析误差产生的原因。
1 气-熔两相流数学模型
1.1 控制方程
在微注射成型过程中,熔体的充填和型腔气体的排出是相互依存的两相流,若排气顺畅,气体的密度将不会有较大变化,熔体和气体均可以看作不可压缩流体,忽略流体的重力,等温熔体流动的控制方程为:

式中 um——熔体流动速度,m/s
ρm——熔体密度,kg/m3
t——充填时间,s
pm——熔体压力,Pa
τm——外应力张量,Pa
气体流动的控制方程为:

式中 ρg——气体密度,kg/m3
ug——气体流动速度,m/s
pg——气体压力,Pa
τg——气体外应力张量,Pa
对于气体,忽略弹性,只考虑黏性,则:

ηg——气体黏度,Pa·s
与纯黏性的气体不同,熔体是黏弹性非牛顿流体,本研究采用单松驰时间谱的PTT模型建立熔体在流动过程中的本构方程[8]:

ξm——材料常数
上随流导数定义为:
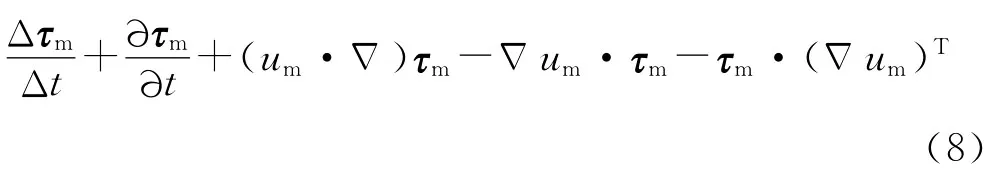
在气-熔界面上,法向上的合力差应等于界面的表面张力(σ):

式中 κ——表面曲率
I——单位矩阵
在模壁上采用滑移边界条件:

式中 β——滑移长度,m
图3、4:作者根据参考文献[11],以及ht t p://designer.home.163.com/case/main/2367/44668.html(即下山建筑平面)进行叠加绘制;
us——壁面滑移速度,m/s
τs——壁面剪切应力,Pa
1.2 界面演化方程
用水平集方法跟踪气-熔界面的移动和演化。定义d(X,Γ)为点X到界面Γ的最短距离,水平集函数φ(X)为点X到界面Γ的符号距离[7],即:

式中 Ωm——熔体区域
Ωg——气体区域
因此,任意时刻气-熔界面即为水平集函数φ(X)的零等值面,界面的法向、曲率可用水平集函数表示为:

界面的演化方程为:

在界面上,考虑表面张力的贡献,两相流的控制方程和本构方程可以统一表示为:Δ
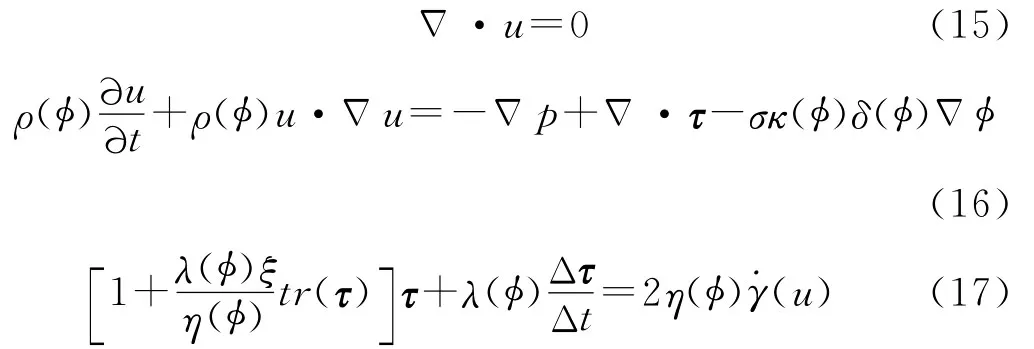
式中 tr——张量的迹,tr(τ)=τxx+τyy+τzz
对应于熔体,变量ρ,p,u,τ分别取ρm,pm,um,τm,气体则取ρg,pg,ug,τg;对于气体区域,本构方程(17)中λ=0,PTT模型简化为纯黏性模型。
为了研究界面的演化与熔体的流速、黏弹性等之间的关系,对上述方程进行无量纲化运算,设:

式中 L——型腔的特征长度,m
U——熔体的特征速度,m/s
将上述变量代入方程(15)~(17),去掉标记“′”后方程变为:
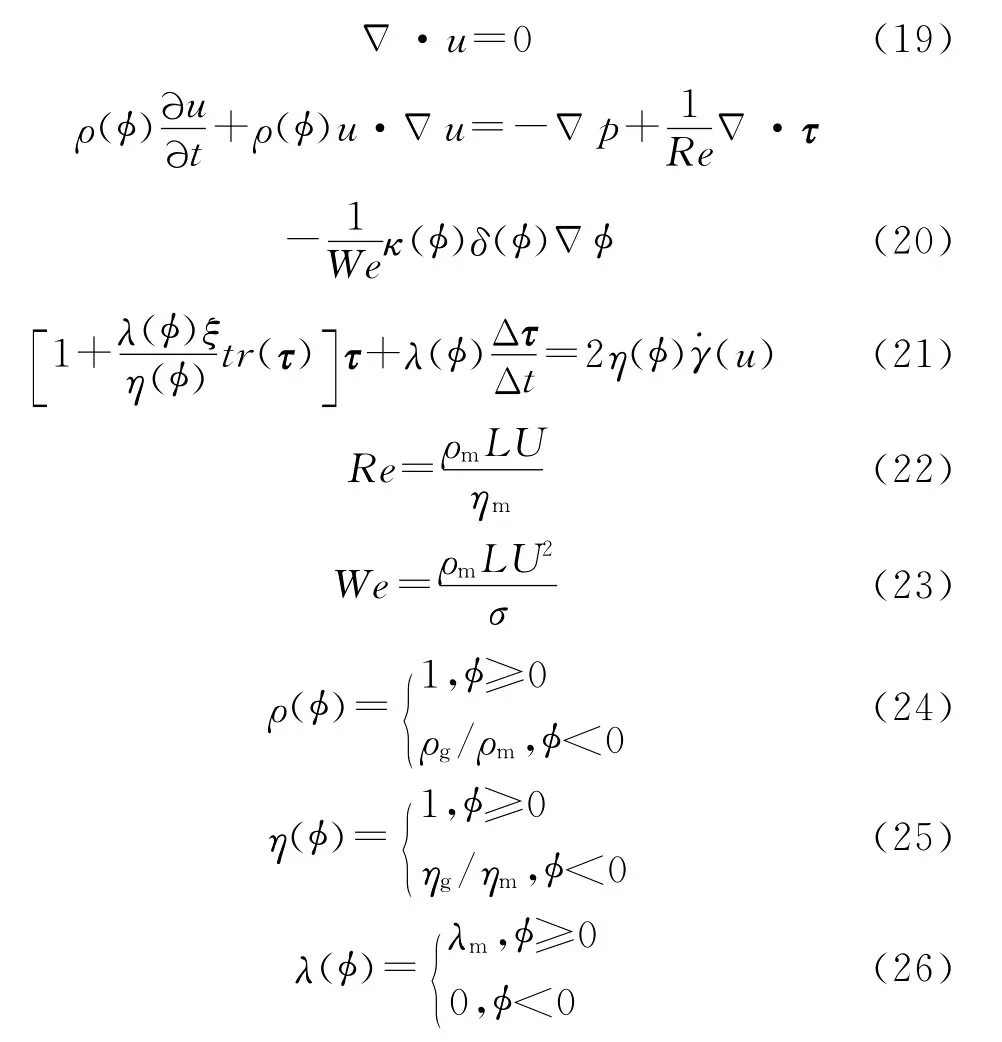
式中 Re——雷诺数
We——韦伯数
ρ(φ)——密度,kg/m3
η(φ)——黏度,Pa·s
λ(φ)——松驰时间,s
2 数值方法
由于微注射成型制品结构复杂,大多没有规则的几何形状,适宜于用有限元法求解成型问题。用检验函数q,v分别乘以方程(19)、(20),再积分得到变分方程:

为了保证数值方法的稳定性,采用DG(Discontinuous Galerkin)方法离散本构方程[9]。用检验函数S双点积方程(7),然后在熔体充填区域积分得:

式中 τext——上游邻接单元应力,Pa
为了保证数值算法的稳定性,插值多项式必需满足 Ladyzenskaya-Babuska-Brezzi条件[9],为此本文采用二阶单元离散速度场,一阶单元离散压力场、应力场,变分方程(27)~(29)离散后为代数方程组(30),是非线性代数方程组,采用Newton-Raphson迭代法求解:
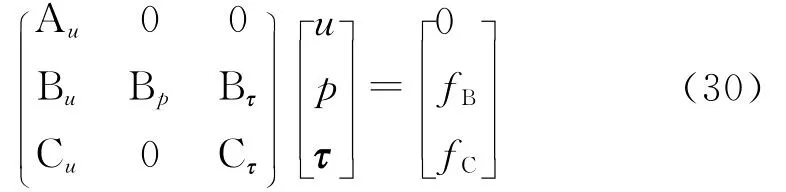
解出速度场之后,用有限元法更新水平集函数,确定前锋面位置。用检验函数r(X)乘界面演化方程(14),再用高斯公式分步积分得到关于水平集函数φ的变分方程:

用一阶单元离散变分方程(31),求出前锋面上的符号距离φ。从方程(31)解出的φ并不总是距离函数,即满足|Δφ|=1,而且,当两界面汇合后φ演化为跳跃函数,所以,需要对φ进行重新初始化。本文采用Sussman方法[10]重新初始化水平集函数,设变分方程(31)的解为φ0,构造初始化求解问题:

式中 tr——参考时间,s
sgn(φ0)——符号函数
ε——网格尺寸的高阶小量,用以保证分母的非奇异
用有限差分法求解问题(32),得到的稳态解即为重新初始化后的水平集函数。
3 实验部分
3.1 模拟材料
模拟材料选用聚甲醛(POM),其主要性能材料参数如表1所示,其中流变性能参数是用旋转流变仪(ARES 2000,Rheometric Scientific,USA)在温度为210℃,载荷为2kg条件下测得。

表1 POM的性能参数Tab.1 Properties parameters of POM
3.2 设备及工艺参数
实验选定的塑料斜齿轮是深圳兆威机电有限公司设计和加工的齿轮箱配件,齿高和齿厚分别为1.08mm和0.73mm,长15mm,如图1所示。将该齿轮应用在微注塑机(Sodic LD30EH20)上,锁模力30kg,最大注射速度800mm/s,成型过程设置的工艺参数如表2所示。

图1 斜齿轮实体模型及尺寸Fig.1 Solid model and dimension of skew gear

表2 斜齿轮加工的工艺条件Tab.2 Process conditions for skew gears
4 结果与讨论
在成型过程中发现在位于浇口一侧壁厚方向上出现气孔,而且重复度很高,任何干燥方法及保压压力都无法避免这一缺陷,说明气孔的形成与材料是否潮湿及收缩无关,是熔体流动过程中裹入气体产生的。同时,缺料注射发现熔体进入底部空腔后出现喷射,如图2所示,说明熔体不再以传统的顺序充填模式充满型腔,充填模式的改变可能是形成气孔的主要原因。本研究以该塑料齿轮成型为研究对象,探索充填模式与注射速度之间的关系,分析气孔的形成机理。塑件脱模后在室温下放置1h,然后沿轴向剖开,确定气孔位置及尺寸。

图2 斜齿轮短射的实验结果Fig.2 Short shot image for skew gears
当熔体以200mm/s速度注射时,入口处雷诺数Re=0.00136、黏性力54300Pa、惯性力1446Pa,黏性力远远大于惯性力,熔体流动处于压力驱动模式,熔体由近到远顺序充满整个型腔,如图3(a)所示。当熔体速度提高1倍,剪切速率也相应增加1倍,受剪切变稀影响,熔体黏度降低了42%,于是,入口处雷诺数Re=0.00468,黏性力63360Pa,惯性力17054Pa,虽然黏性力仍大于惯性力,但属于同一量级,惯性力的作用逐渐显现,与低速流动相比,惯性力使熔体沿流长方向前进了更长的距离,如图3(b)所示。当熔体流速提高到800mm/s时,剪切速率进一步增大,黏度降低了66%,入口处雷诺数上升到0.016、黏性力73992Pa、惯性力173349Pa,惯性力大于黏性力,熔体在惯性力作用下快速向前充填,进入较大空腔后呈喷射状态,快速达到型腔末端,如图3(c)所示。由此可见,注射成型充填过程中聚合物熔体的流动形态是黏性力与惯性力相互竞争的结果,与注射速度、型腔尺寸、材料特性等密切相关,对于给定的材料及制品尺寸,当注射速度提高到某一临界值后,熔体将冲破黏性力的束缚转入喷射充填模式。虽然控制方程中加入了表面张力的贡献,但只有当塑件尺寸足够小时表面张力效应才会显著,对于本文研究的塑件,表面张力在斜齿上达到最大(132Pa),但远小于黏性力和惯性力,对充填速度、流动模式基本没有影响。

图3 不同注射速度时的充填模式.Fig.3 Filling mode corresponding to different filling speed
当熔体以800mm/s高速进入型腔时,惯性力较大,占主导地位。由于齿轮上部厚度较小(1.65mm),受边界上黏性力束缚熔体仍然向横向充填,但在流动方向充填的长度大于横向充填宽度。而熔体进入较大空腔后(带齿厚度2.6mm),流动处于惯性驱动模式,熔体以较细的射流喷入型腔,由于网格不完全对称,熔体喷射出现了轻微摆动。随着流长的增长和温度的降低,流动阻力增大,流速减小;另一方面,浇口周围的压力增大,压力梯度也随之增大,熔体在压力驱动下向周围空腔充填,所以,充填呈现出喷射与顺序注射共存的现象,如图4(a)所示。熔体到达底部后开始堆积,形成反向充填,位于浇口一侧熔体流速较快,反向充填速度、充填体积也较大,易形成锯齿状流动前沿,如图4(b)所示。随着充填熔体的增多,充填阻力持续增加,充填速度逐渐下降,惯性力降低,流动又回到压力驱动模式,熔体按距离浇口远近由近到远顺序向前充填,并与前期喷射的熔体汇合,在交汇处空隙较大的地方形成裹气,如图4(c)所示。当熔体持续充填,将型腔中的气体挤压至流动末端,由分模面排出,同时将不能顺畅排出的气体包裹形成气孔,如图4(d)所示。

图4 高速(800mm/s)充填过程中熔体前沿的演化Fig.4 Evolution of melt front advancement during filling stage of high speed injection(800mm/s)
从以上分析及模拟结果可以看出,裹气的形成与注射速度有密切关系。当注射速度较低时,惯性力比黏性力小,熔体处于顺序充填模式,全部气体从分模面排出,不会形成裹气。只有当注射速度足够大时,惯性力才大于黏性力,形成喷射,也只有喷射足够强时,熔体射到底部后才能持续堆积,形成反向充填,与后续顺序充填的熔体汇合形成裹气。同时,位于浇口一侧的反向充填、顺序充填速度均高于其他位置,反向充填速度越高越易于形成锯齿状的流动前沿,产生较大的孔隙,也易于与后续高速顺序充填的熔体在边界处汇合形成空腔,从而包裹其中的气体,形成气孔。因此,只有高速注射时,熔体才能改变顺序充填模式,在反向充填与顺序充填最前端的前锋面处形成裹气,如图5(a)所示。采用本研究方法模拟的气孔位置与实际加工的气孔位置[见图5(b)]基本一致,然而,由于本研究数学模型中没有考虑气体的可压缩性及计算熔体密封气体之后的充填及保压阶段熔体持续流动产生的气孔变形,所以模拟的气孔形状与实际结果有差异。
5 结论
(1)当注射速度达到某一临界值后,惯性力大于黏性力,熔体在流动方向的充填速度大于横向充填速度,并在较大空腔处形成喷射,微注射成型中熔体的流动模式与材料特性、型腔尺寸和注射速度密切相关;

图5 模拟的气孔位置与实际加工的气孔位置Fig.5 Air trap locations with simulation and manufacture
(2)在高速微注射成型的充填初期,熔体的速度高、惯性大,熔体以喷射的方式流入较大空腔,由于微成型制品尺寸较小,熔体快速喷至型腔末端,并开始堆积,形成反向充填;随着流动阻力的增大,熔体流动速度降低,熔体流动又转向常规的顺序充填,反向充填与顺序充填的熔体前沿在汇合处包裹空气,形成气孔。
[1] D Yao,B Kim.Simulation of the Filling Process in Microchannels for Polymeric Materials[J].J Micromech Microeng,2002,12:604-610.
[2] S W Kim,L S Turng.Three-dimensional Numerical Simulation of Injection Molding Filling of Optical Lens and Multi-scale Geometry Using Finite Element Method[J].Polymer Engineering and Science,2006,46:1263-1274.
[3] S J Choi,S K Kim.Multi-scale Filling Simulation of Micro-injection Molding Process[J].J Mechanical Science and Technology,2011,25(1):117-124.
[4] W Cao,S Gan,S Ye,et al.Study on Air Accumulation and Influence on Flow Balance in Micro-injection Molding[J].J Manufacturing Science and Engineering,2011,133:401-406.
[5] C A Griffiths,S S Dimov,S Scholz,et al.Cavity Air Flow Behavior During Filling in Microinjection Molding[J].J Manufacturing Science and Engineering,2011,133:601-610.
[6] 李帅君,熊守美.应用两相流模型模拟压铸充型过程的卷气现象[J].金属学报,2009,45(10):1153-1158.Li Shuaijun,Xiong Shoumei.A Two-phase Flow Model for Simulaiting Air Entrapment During Mold Filling of High Pressure Die Casting Process[J].Acta Metallurgica Sinica,2009,45(10):1153-1158.
[7] 张明远,陈立亮,庞盛永,等.基于投影-水平集方法充型过程气-液两相流数值模拟[J].铸造,2010,59(5):478-481.Zhang Mingyuan,Chen Liliang,Pang Shengyong,et al.Numerical Simulations of Gas-liquid Two-phase Flow During Filling Process Based on Projection Level Set Method[J].Foundry,2010,59(5):478-481.
[8] G W M Peters,F P T Baaijens.Moldeling of Non-isothermal Viscoelastic Flows[J].J Non-Newtonian Fluid Mechanics,1997,68:205-224.
[9] Arjen C B Bogaerds,Wilco M H Verbeeten,Gerrit W M Peters,et al.3DViscoelastic Analysis of a Polymer Solution in a Complex Flow[J].Comput Methods Appl Mech Engrg,1999,180:413-430.
[10] M Sussman,P Smereka,S Osher.A Level Set Approach for Computing Solutions to Incrompressible Two-phase Flow[J].J Comput Physics,1994,114:146-159.
Study on Melt Filling Mode and Trapping Air Mechanism in High Speed Micro-injection Molding
ZHANG Shixun1,CAO Wei1,YE Shubing2,LI Qian1,SHEN Changyu1
(1.APPT NERC,Zhengzhou University,Zhengzhou 450002,China;2.Shenzhen Zhaowei Machinery and Electronics Co,Ltd,Shenzhen 518103,China)
In order to simulate the melt flow and melt front more precisely,mathematic models of coupled melt and air flows were formulated in terms of two phase flow theory.A viscoelastic model rather than conventional viscous model was employed to represent the relationship between stress and shear rate.The melt front was tracked using level set method.Based on the proposed mathematic models and numerical methods,three types of flows and filling modes for low-,medium-,and high-speed micro-injection molding were investigated.In addition,the mechanism of air-trapping was analyzed and the possible location of trapped air was predicted.To verify the validity of the proposed method,a skew gear was designed and manufactured using high speed micro-injection molding.The actual trapped air location was in good agreement with the simulated results.This study showed that the filling mode depended on injection speed,material characters,and cavity size.The air-trapping was likely to occur at the jetting mode.
micro-injection molding;two phase flow;filling mode;viscoelastic model
TQ320.66+2
B
1001-9278(2012)01-0065-06
2011-10-28
国家自然科学基金资助项目(10872185);河南省重大公益项目[HNZB(2010)N91号]
联系人,zsxzzu@zzu.edu.cn
(本文编辑:赵 艳)

