切入磨削与纵向磨削的磨削力分析与比较
李 厦 李郝林
上海理工大学,上海,200093
0 引言
磨削加工技术是先进制造技术中的重要内容,磨削加工的品质往往决定着工件的最终加工精度。外圆磨削是一种主要的磨削方式,它包括切入磨削(plunge grinding)和纵向磨削(traverse grinding)。切入磨削时,砂轮与工件之间只有径向运动;纵向磨削时,砂轮与工件之间既有径向运动又有轴向运动,适用于工件长度大于砂轮宽度的情况,并且比切入磨削复杂。
磨削过程的在线监控对提高磨削加工质量有重要意义,因此国内外学者均对此进行了大量的研究。在线监控利用的主要信号有磨削力、电流、功率、声发射和振动信号等[1-2]。目前,对外圆磨削监控的研究主要局限为单一的外圆磨削方式,要么是切入磨削,要么是纵向磨削[3-4],而对两者进行比较研究的文献较为鲜见。本文分析了同一工况下的切入磨削和纵向磨削(先切入磨削后纵向磨削的情况),并针对纵向磨削,在传统阶梯模型的基础上提出了砂轮磨损的抛物线模型,并分析了两种模型下的切向磨削分力,推导了比较公式,利用砂轮主轴功率信号验证了研究结果。
1 外圆纵向磨削砂轮磨损
纵向磨削相比切入磨削最大的区别是加工过程中砂轮的径向磨损是变化的。外圆纵向磨削过程如图1所示。
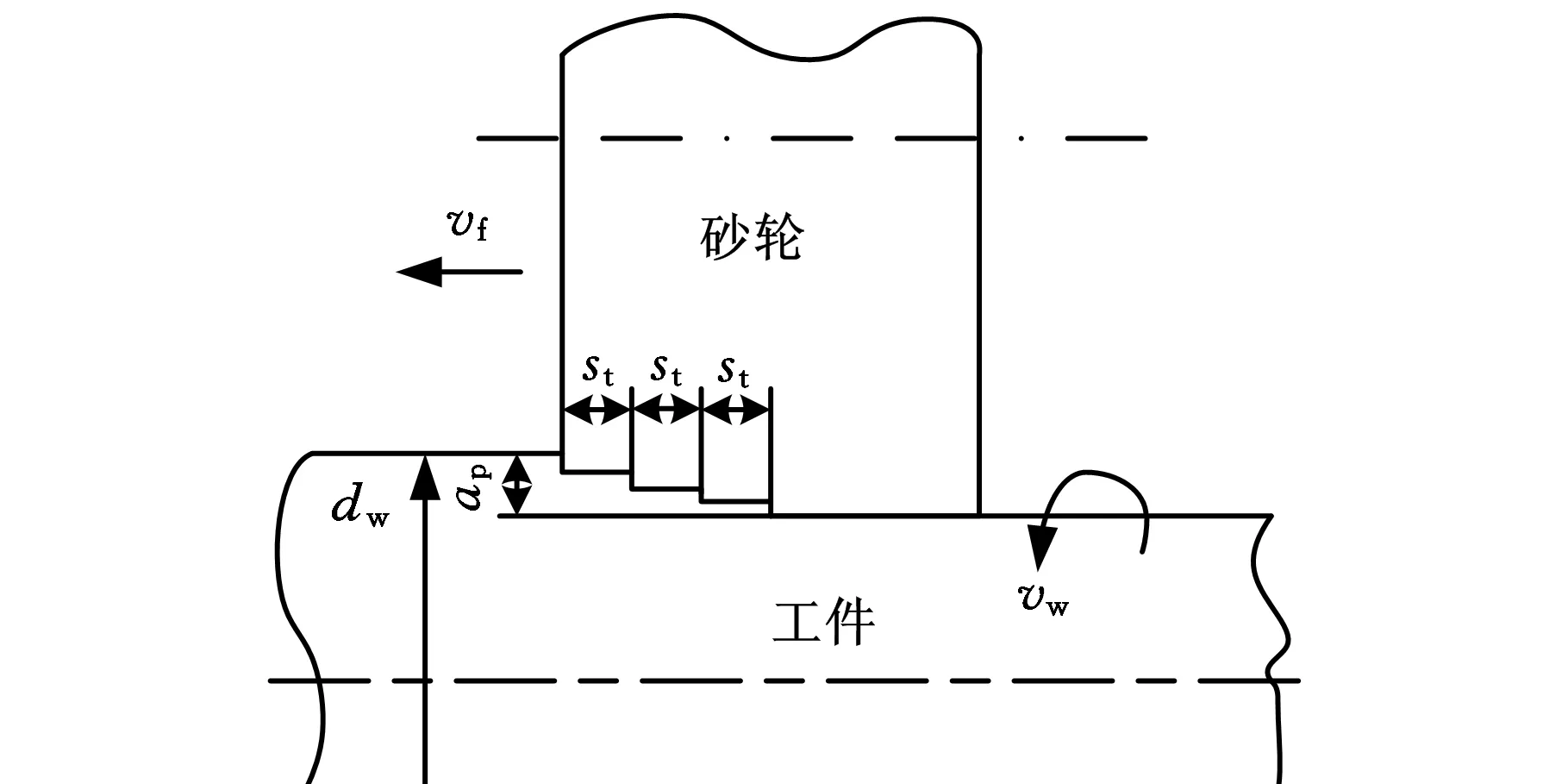
图1 外圆纵向磨削示意图
工件每旋转一周的进给量st为
(1)
式中,dw为工件直径;vw为工件线速度;vf为砂轮纵向进给速度;nw为工件转速。
文献[5]最早研究了纵向磨削的砂轮磨损情况,并提出了纵向磨削砂轮磨损的阶梯模型,由于有砂轮磨损存在,切深的一部分将在砂轮的下一转中留给和前缘st宽度相邻近的第二个st宽度的砂轮来去除,砂轮的磨损同样又引起砂轮宽度上的第3个st部分的磨除作用,并以此类推。砂轮越靠前缘的部分磨除金属越多,自身磨损也越快,按st的大小把砂轮沿宽度方向分成若干等分段,对于被加工工件的同一部分而言,砂轮的各等分段将依次对它进行磨削。
设砂轮的切深是ap,因此起始台阶的砂轮径向切深最大值为ap,后面台阶的切深都小于ap,假设一共有k个台阶,第j级台阶砂轮径向切深为apj,根据工件表面粗糙度要求,第k台阶的砂轮径向切深apk=0[6],因此纵向磨削可以看作宽度为st的k-1个砂轮做切深递减的切入磨削。将砂轮等效成宽度相等的k-1个小砂轮是后面进行比较研究的基础。
由于实际纵向磨削砂轮磨损的形状不是阶梯形,而是曲线形的[5-6],因此在传统的阶梯模型基础上,本文提出以抛物线来模拟实际曲线的研究模型(简称抛物线模型),并分别对以阶梯模型和抛物线模型表示的纵向磨削与切入磨削进行比较研究。
2 磨削力比较
2.1 磨削力
对于外圆切入磨削,磨削力可分为切向分力Ft和法向分力Fn,对于外圆纵向磨削,还应附加上一个平行于砂轮主轴的纵向进给磨削分力Fs,如图2所示。对于Fs来说,虽然从一个磨粒的角度来看, 这个分力应该是很大的,但由于各磨粒具有随机分布的正负磨削力倾角, 会使其各分力相互抵消,因此总磨削分力Fs的值不会很大[7],分析时一般不考虑Fs。

图2 纵向磨削加工中的磨削力
研究磨削力的文献较多[8-10],以磨削切向分力为例,其经验表达式如下:
(2)
de=dwds/(dw±ds)
式中,K、α、β、γ均为磨削力因数;vs为砂轮线速度;de为砂轮当量直径;ds为砂轮直径。
法向分力一般大于切向分力,并且二者成比例关系。根据式(2)可以看出,磨削切向分力Ft主要与砂轮线速度vs、工件线速度vw、砂轮当量直径de和磨削切深ap有关。因此,从易于测量的角度出发,只需分析磨削切向分力,就可很容易得出磨削力。对于在同一工况下的先切入磨削后纵向磨削的情况,vw、vs和de是相同的,不同的是磨削切深ap。因此,可以将磨削切向分力公式简化为
(3)
磨削切向分力Ft的测量是通过测量磨削功率来实现的。由于工件的线速度远小于砂轮的线速度,因此磨削功率P可简化表示为
P=Ftvs
(4)
在已知vs的情况下,通过测量磨削功率P,即可间接获得磨削切向力Ft。下面主要比较切入磨削情况下的切向分力和纵向磨削情况下的切向分力。
2.2 切入磨削的切向分力
由于将砂轮看成是由k-1个小砂轮组成的,则切入磨削时的每个小砂轮的切深都是ap,其切向分力用F′t表示,则切入磨削的切向分力总和为
(5)
2.3 纵向磨削的切向分力
2.3.1阶梯模型的切向分力
将图2中的砂轮放大,为了进行近似的定量分析,假设阶梯的倾斜角度为定量,如图3所示。L为砂轮宽度,Lk为砂轮前缘到第k级台阶宽度,此处砂轮切深为0,ψ为砂轮磨损形成的斜面角度。分析中不考虑由于工件是细长杆件而引起的支架和工件的弹性变形,也不考虑工件和砂轮的接触变形。
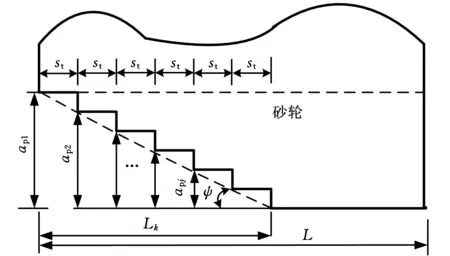
图3 阶梯模型砂轮切深示意图
取ap=ap1,Lk=L,此时整个砂轮都参与纵向磨削,切向磨削分力最大。根据图3可以推得
(6)
用F″表示纵向磨削的切向分力,则纵向磨削的切向分力总和为
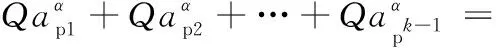
(7)
由于st/L≪1,因此将幂函数用泰勒级数展开,忽略高阶项,得
(8)
将k=L/st代入式(8),得
(9)
则切入磨削与阶梯模型的纵向磨削的切向分力之比为
(10)
2.3.2抛物线模型的切向分力
纵向磨削砂轮磨损的抛物线模型如图4所示,以砂轮轴向方向为x轴(图4中x方向为正方向),以砂轮径向方向为y轴,建立砂轮切深抛物线方程y2=2px,推导时取最大切向分力,即ap=ap1,Lk=L。
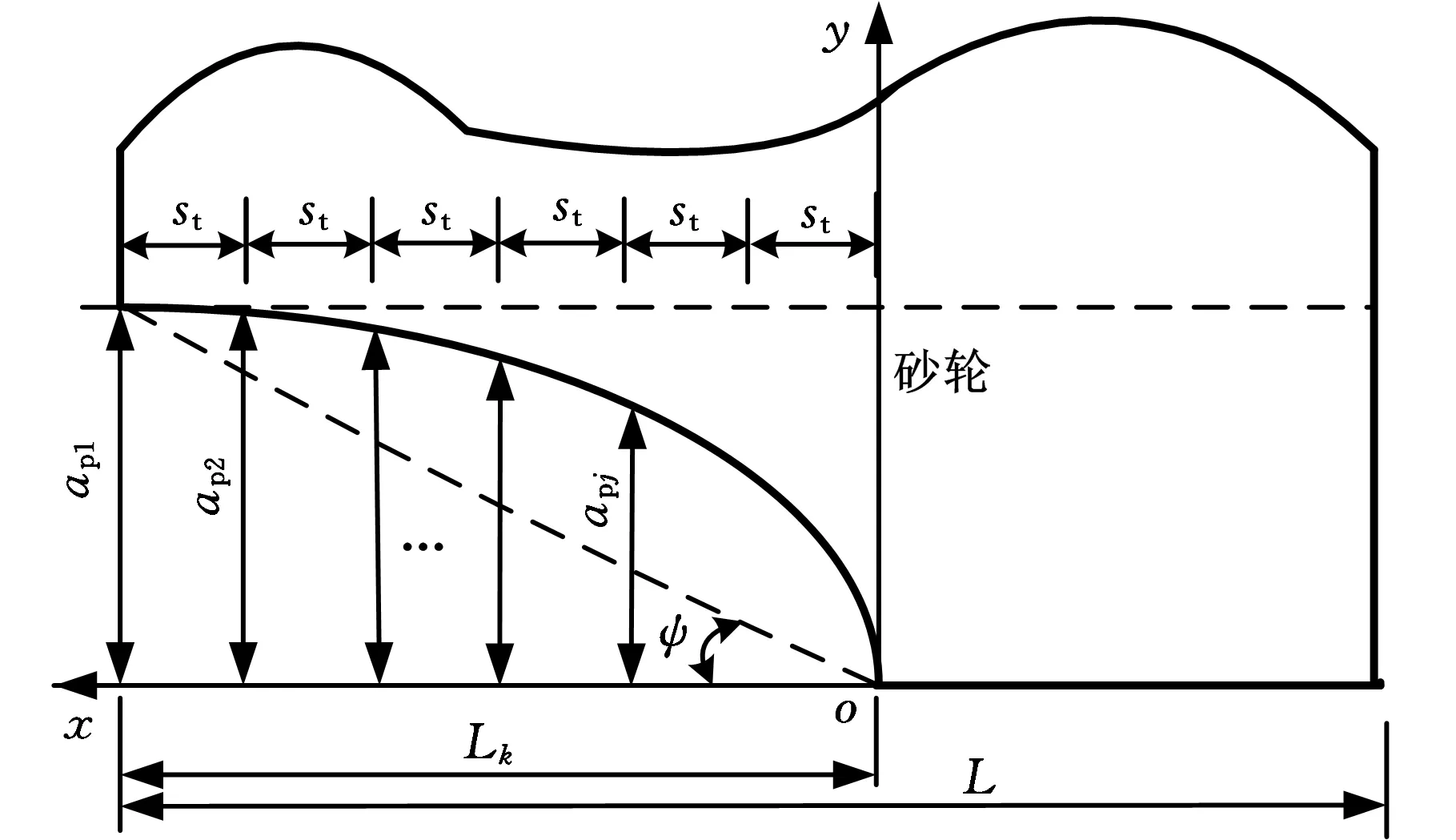
图4 抛物线模型砂轮切深示意图
则
每个小砂轮的切深用抛物线的前点表示,则根据抛物线方程可得每个小砂轮的切深:
(11)
那么纵向磨削的切向分力总和为
(12)
由于st/L≪1,因此将幂函数用泰勒级数展开,忽略高阶项,得
(13)
将k=L/st代入式(13),得
则切入磨削与抛物线模型的纵向磨削的切向分力之比为
(14)
3 实验验证
磨削实验是在德国斯来福临公司的K-C33数控内外圆磨床上进行的。磨床的主轴转速为1~1500r/min,最小进给量为0.1μm;砂轮型号为53A80L15V,宽度为62mm,直径为440mm;实验试件为圆柱体,直径为61.5mm,长度为120mm,材料为45钢,加工时通过双顶尖将其固定;冷却液为嘉实多Hysol R水基磨削液。试件的加工现场如图5a所示。
电流或功率信号常用于刀具磨损检测[11-12],也可用于切削力间接获得过程中[13-14]。本文采用的功率传感器型号为 Power Cell PH-3A,安装在电气柜内,与砂轮电机(EMWB F200L))的三相线连接如图5b所示。采集板卡型号为Spectrum M1.3120(2通道,12位A/D转换),采集软件为DEWESoft(版本6.31SE),功率信号采样频率为10kHz。

(a)试件加工现场(b)功率传感器图5 试件加工现场和功率传感器
磨削方式为多次切入走刀磨削,其过程如下:砂轮与工件端部对齐,先切入磨削,然后纵向磨削,到另一端部再切入磨削,然后再纵向磨削。对应的磨削过程为粗磨→半精磨→精磨→光磨,以纵向进给速度即走刀速度分别为100mm/min、200mm/min和400mm/min来采集实验数据,每个纵向进给速度下重复做三次,共采集9组实验数据。半精磨的切深分别为4μm和2μm,精磨的切深分别为2μm和1μm。工件转速为100r/min;砂轮线速度为35m/s。
通过DEWESoft软件采集的原始数据如图6所示,可以看出,切入磨削有明显的峰值,切入磨削和纵向磨削连续交替进行。
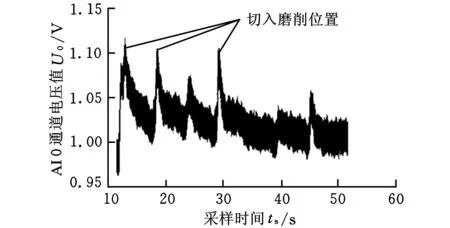
图6 功率信号波形图
砂轮电机功率信号中, 不可避免地含有种种干扰。根据信号的频谱图,主要的干扰有砂轮转速干扰、50Hz工频干扰,这些干扰常常使测量信号的波动过大。因此,为了进行准确的测量和监控必须消除被测信号中的干扰。首先,对信号进行切比雪夫低通滤波,截止频率为10Hz,切入磨削取功率采样电压RMS值的峰值,纵向磨削根据3σ准则去除突变信号[14],然后取功率采样电压RMS值的平均值。分别分析了不同进给量(4μm、2μm、1μm)和不同纵向进给速度(400mm/min、200mm/min、100mm/min)情况下的切入磨削和纵向磨削功率信号,纵向进给速度、切深和功率采样电压RMS值关系如图7所示。可以看出,功率采样电压RMS值与纵向进给速度成正比,同等工况下,切入磨削力大于纵向磨削力,随着纵向进给速度的增加,切入磨削的功率采样电压RMS值变化大于纵向磨削的功率采样电压RMS值。
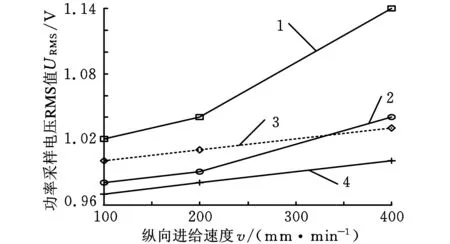
1.切入磨削,切深2μm 2.纵向磨削,切深2μm3.切入磨削,切深1μm 4.纵向磨削,切深1μm图7 纵向进给速度、切深和功率采样电压RMS值关系图
根据切入磨削和纵向磨削的功率采样电压RMS值,求出其比值,根据经验,磨削系数α取0.4,以切深2μm为例,实验数据与理论值的比较见表1。从表1可以看出,抛物线模型的准确率高于阶梯模型的准确率,切入磨削和纵向磨削的切向分力的理论比值随着纵向进给速度的增大而增大,实验数据的比值随着纵向进给速度的增大而减小。
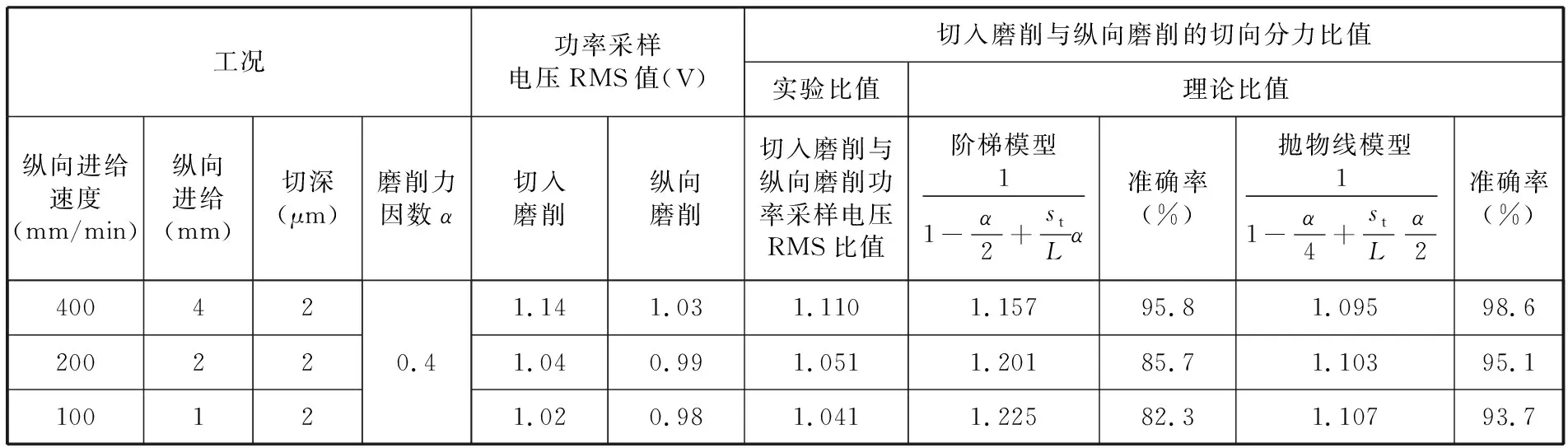
表1 实验数据与理论值比较表
4 结论
(1)由式(10)、式(14)和图7可知,切入磨削与纵向磨削的切向分力比值与磨削力因数、砂轮宽度和纵向进给量有关,同等工况下,由于切深的原因,切入磨削力大于纵向磨削力。
(2)实验结果证明:纵向磨削的抛物线模型相比阶梯模型更接近实际情况,当纵向进给速度分别为100mm/min、200mm/min、400mm/min时,其准确率分别为98.6%、95.1%和93.7%,高于阶梯模型的95.8%、85.7%和82.3%。
(3)砂轮纵向进给速度减小,使磨削切向分力减小,砂轮主轴功率减小。切入磨削和纵向磨削的理论比值随着纵向进给速度的增大而增大,实验数据的比值随着纵向进给速度的增大而减小,其原因有待于进一步分析。
[1] Liang S Y,Hecker R L,Landers R G.Machining Process Monitoring and Control: the State-of-the-art[J].Journal of Manufacturing Science and Engineering, Transactions of the ASME, 2004,126:297-310.
[2] Abellan-Nebot J V,Romero Subiron F.A Review of Machining Monitoring Systems Based on Artificial Intelligence Process Models[J].International Journal of Advanced Manufacturing Technology, 2010,47:237-257.
[3] 丁宁.外圆纵向智能磨削研究[D].长春:吉林大学,2004.
[4] Kruszynski B W,Lajmert P.An Intelligent System for Online Optimization of the Cylindrical Traverse Grinding Operation[J].Journal of Engineering Manufacture,2006,220(3):355-363.
[5] Verkerk J.Plunge Grinding Data for the Control of Traverse Grinding Operations[C]//North Am Manuf. Res. Conf. Proc., 8th.Rolla:Manufacturing Engineering Transactions,1980:80-98.
[6] 庄司克雄.磨削加工技术[M].郭隐彪,王振忠,译.北京:机械工业出版社,2007.
[7] 臼井英治.切削磨削加工学[M] .高希正, 刘德忠,译.北京:机械工业出版社,1982.
[8] Patnaik D,Singh V,Rao P V.A New Model for Grinding Force Prediction and Analysis[J].International Journal of Machine Tools and Manufacture,2010,50:231-240.
[9] Liu Q,Chen X,Wang Y, et al.Empirical Modelling of Grinding Force based on Multivariate Analysis[J].Journal of Materials Processing Technology,2008,203:420-430.
[10] 张建华,葛培琪,张磊.基于概率统计的磨削力研究[J].中国机械工程,2007,18(20):2399-2402.
[11] Li X L,Guan X P.Time-frequency-analysis-based Minor Cutting Edge Fracture Detection During and Milling[J].Mechanical Systems and Signal Processing,2004,18:1485-1496.
[12] Gangopadhyay A,Barber G,Zhao H.Tool Wear Reduction Through an Externally Applied Electric Current[J].Wear,2006,260:549-553.
[13] 李斌,张琛,刘红奇.基于主轴电流的铣削力间接测量方法研究[J].华中科技大学学报(自然科学版),2008,36(3):5-7.
[14] 焦阳,李郝林.数控磨削过程中砂轮电机电流的实时监测[J].上海理工大学学报,2009,31(1):77-79.

