基于最大树聚类的多超球体一类分类算法及其应用研究

刘丽娟 陈 果

南京航空航天大学，南京，210016

0 引言

相对于多类分类算法对样本数量的要求较高，一类分类[1-4]方法仅仅需要一类样本对象。如状态监测与故障诊断运行状态中，相对于大量正常状态的样本，异常状态的样本往往很少，而且表现出各种各样的异常模式[5]，而其主要任务是识别状态正常与否，采用一类分类法就能有效解决该问题。

一类分类器仅需一类样本通过机器学习生成一个闭合的超球体作为该类样本的决策边界。如果测试样本点在超球体的外面，则认为这些样本点是异常样本(野点)，反之则判断为正常样本。但是在实际应用中发现，即使是正常状态的训练样本，在数据分布或者结构信息上还是会存在差异(特别是当训练样本的数据是成簇分布时)，如果只按照单超球体一类分类建模，那么构造的单个超球体不仅包围了训练数据，而且还包围了簇间的空白区域[6]，这样一来很可能将非正常的样本也错误地判为正常样本。虽然通过引入核函数，调节核参数(如高斯核参数)可以使上述情况有所改善，但是这无法从根本上解决问题。因此本文采用多个超球体来覆盖训练样本，研究了基于最大树聚类的多超球体[7-8]一类分类器，分别将该方法应用于仿真数据、UCI标准数据集以及转子故障诊断三个实例中，并且与常用的基于单超球体的一类分类方法进行了比较，结果表明了该方法的有效性。

1 单超球体一类分类器

一类分类器针对一类对象(如故障诊断中的正常运行状态，为正类)，而相对于该类对象的其他对象(如故障诊断中的非正常运行状态，为负类)统称异常对象(野点)。单超球体一类分类器本质上是寻找一个能够包含全部正类样本的最小超球体，在球体外的点视为野点。设有一个正类样本集{x1，x2，…，xN}，将该正类样本集全部样本包围的最小球体的半径设为R，球心设为a,为了实现错误划分和区域范围之间的折中，在优化过程中引入松弛变量，此时样本集满足：

(1)

定义Lagrange函数：

(2)

其中，C为惩罚因子，ξi为对应第i个样本的松弛变量，Λ={αi}，对应的Lagrange系数αi≥0，γi≥0。将式(2)分别对R和α求偏微分，并令其等于0，得到相关的优化方程如下：

(3)

引入高斯径向基核函数K(x,y)，即

(4)

用核函数K(x,y)替代(x,y)，得到对应的优化方程：

(5)

实际上，根据KKT(Karush-Kuhn-Tucker)条件，大部分αi为0，只有一小部分αi>0，而与这些不为零的αi所对应的样本点决定了超球体边界的构成，为此，将这些样本点称为支持对象(support objection)。

对于待定状态数据z，其到球心的距离的平方为

(6)

取任一支持对象xs，则球体半径的平方为

(7)

依据下式可判断z是否为正类样本：

(8)

2 基于最大树聚类的多超球体一类分类器

单超球体一类分类器在进行建模时，没有考虑到样本间的分布结构以及同类样本之间存在的差异，因此本文采用多超球体来代替单超球体覆盖训练样本。图1中，“o”表示的是正常样本，“*”表示的是异常样本。图1a所示是采用单超球体覆盖训练样本的示意图，图1b所示是采用多超球体覆盖训练样本的示意图。通过比较发现图1b的方法较之于图1a的方法具有更高的识别率。

(a)单超球体

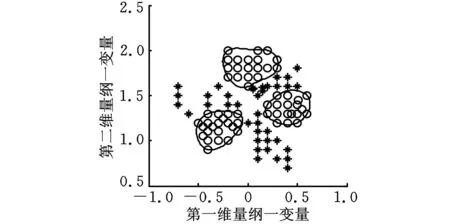
(b)多超球体图1 单超球体与多超球体比较图

相对于单超球体的一类分类器，多超球体一类分类器首先要对训练样本进行聚类，然后对聚类后的各子类分别进行一类支持向量机分类器学习，最后得到对应的多个超球体一类分类模型。

2.1 聚类

本文采用最大树[9-10]聚类算法进行聚类。用绝对值减数法：

(9)

2.2 基于最大树聚类的多超球体一类分类法流程

基于最大树聚类的多超球体一类分类法具体的过程如下：

(1)对所得样本数据进行特征提取，得到对应的训练样本集、测试样本集。

(2)将训练样本集按最大树聚类算法聚为多个子类。根据所聚成的子类个数将训练样本集的各个子类分别进行一类支持向量机分类器学习，得到各个子类所对应的单超球体，各子类对应的单超球体相组合就构成对应于训练样本集的多超球体一类分类模型。

(3)采用得到的多超球体一类分类模型对测试样本集进行决策。只要存在一个超球体能包含测试样本，就将该测试样本视为正常类；若没有一个超球体能包含该测试样本，就将该测试样本视为异常类。

图2是其对应的流程图，可以看出当训练样本集聚类为一个子类(即m=1)时，所得的多超球体分类模型就是单超球体分类模型。即单超球体一类分类器可以看作是多超球体一类分类器将其对应的训练样本集聚为一个子类的特例。

图2 算法流程

3 实验与应用

3.1 仿真数据实验

为了验证基于最大树聚类的多超球体一类分类法的可行性，本文首先选用图1所示的具有聚类特性的仿真数据进行验证。从图1可以看出，正常样本聚类特征明显，倾向于聚为3个子类。

随机选择正常样本的2/3作为训练样本，剩余的1/3样本作为正类测试样本，所有的异常样本作为负类测试样本。采用最大树聚类法(α取0.5)，选取聚类子类数10以内对应的结果，如图3所示。根据图3a所示的参数λ与聚类后子类数c的关系,图3b所示的误差平方和Je与聚类后子类数c的关系，选取参数λ=0.88，聚类后聚为3个子类，这一点与图1中样本簇分布的趋势一致。

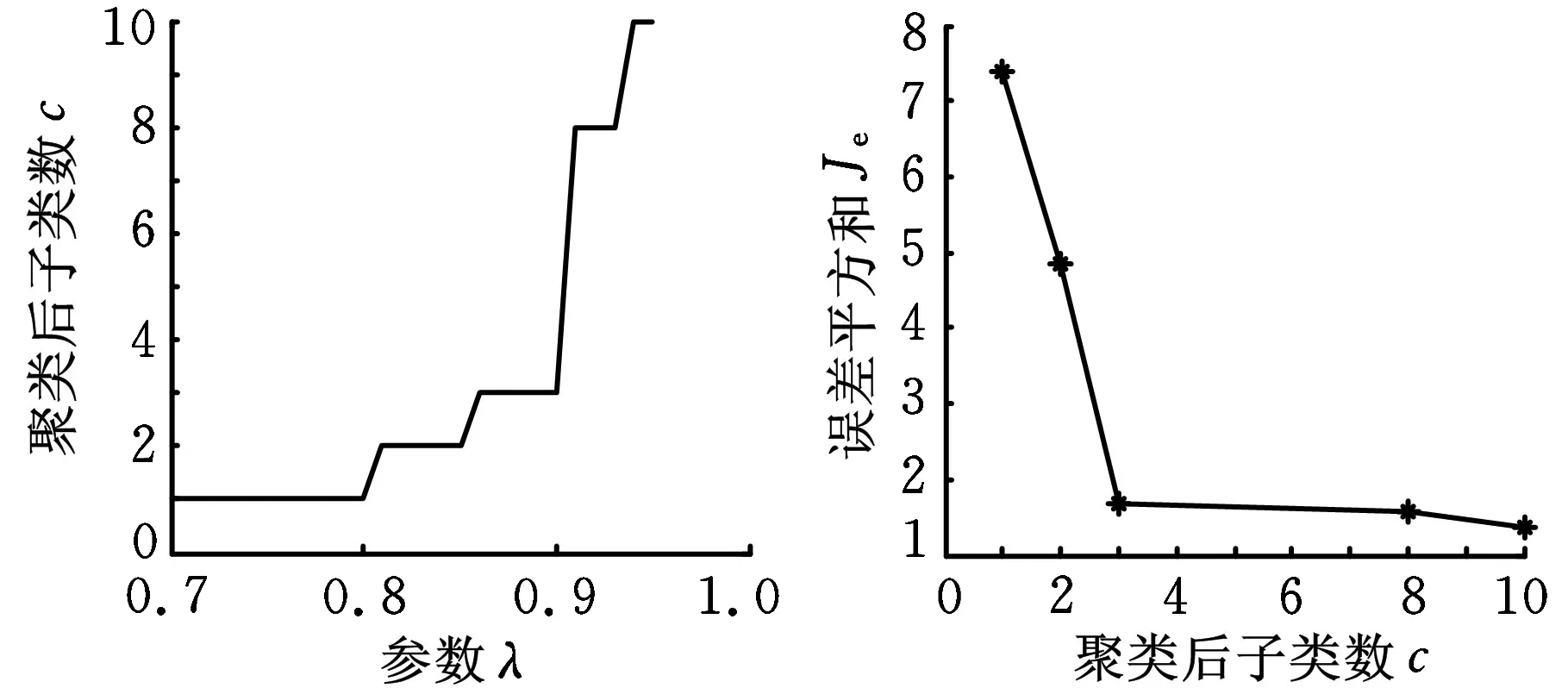
(a)参数λ与子类数关系(b)子类数与误差平方和关系图3 仿真数据聚类结果

根据聚类的结果，分别采用单超球体一类分类器和多超球体一类分类器进行学习，两种算法中涉及的惩罚因子C与高斯核参数σ，均采用文献[12-14]中提到的粒子群优化算法对其进行参数自适应优化。两种算法在最优参数下得到的识别率如表1所示。其中，T为正类训练样本数；T1为正类测试样本数；T2为负类测试样本数；N为支持向量个数；R1为正类识别率；R2为负类识别率；R为平均识别率，R=(R1+R2)/2。

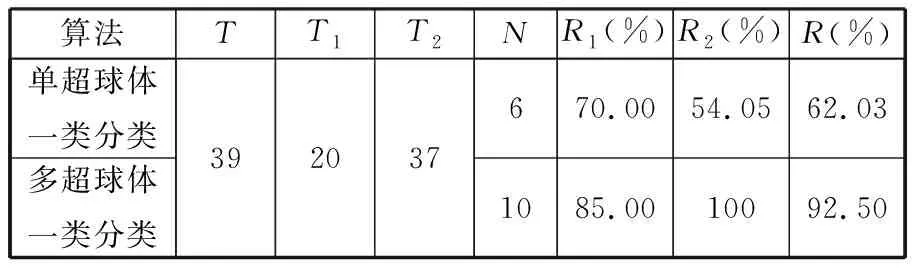
表1 多超球体一类分类器与单超球体一类分类器对仿真数据的实验结果

表1所示结果表明，当训练样本呈聚类特征分布时，多超球体一类分类算法相对于单超球体一类分类算法具有优越性。

3.2 UCI标准数据集实验

为了进一步验证该算法的可行性。本文选取UCI数据库中的Sonar这个两类数据集产生两个单类数据来验证。获取的Sonar数据集包含两类，分别记为Sonar1、Sonar2。首先对获取的数据在信息量保持0.95的情况下，得到主成分分析(principle component analysis，PCA)特征压缩后的两类样本数据。图4a与图4b分别是部分Sonar1和Sonar2数据取最大3维主分量的可视化分布图，从一定程度上反映了高维数据簇分布的趋势。

和仿真实验中一样，分别针对每一类样本集，随机选取其中的2/3样本作为正类训练样本，剩余的1/3同类样本作为正类测试样本，另一类的1/3样本作为负类测试样本。图5、图6分别是对Sonar1及Sonar2采用最大树聚类法(α取0.2)，对应聚类子类数10以内的结果。因此Sonar1、Sonar2分别取：参数λ=0.87、聚类后聚为3个子类以及参数λ=0.88、聚类后聚为3个子类。

(a)Sonar1 样本三维分布图

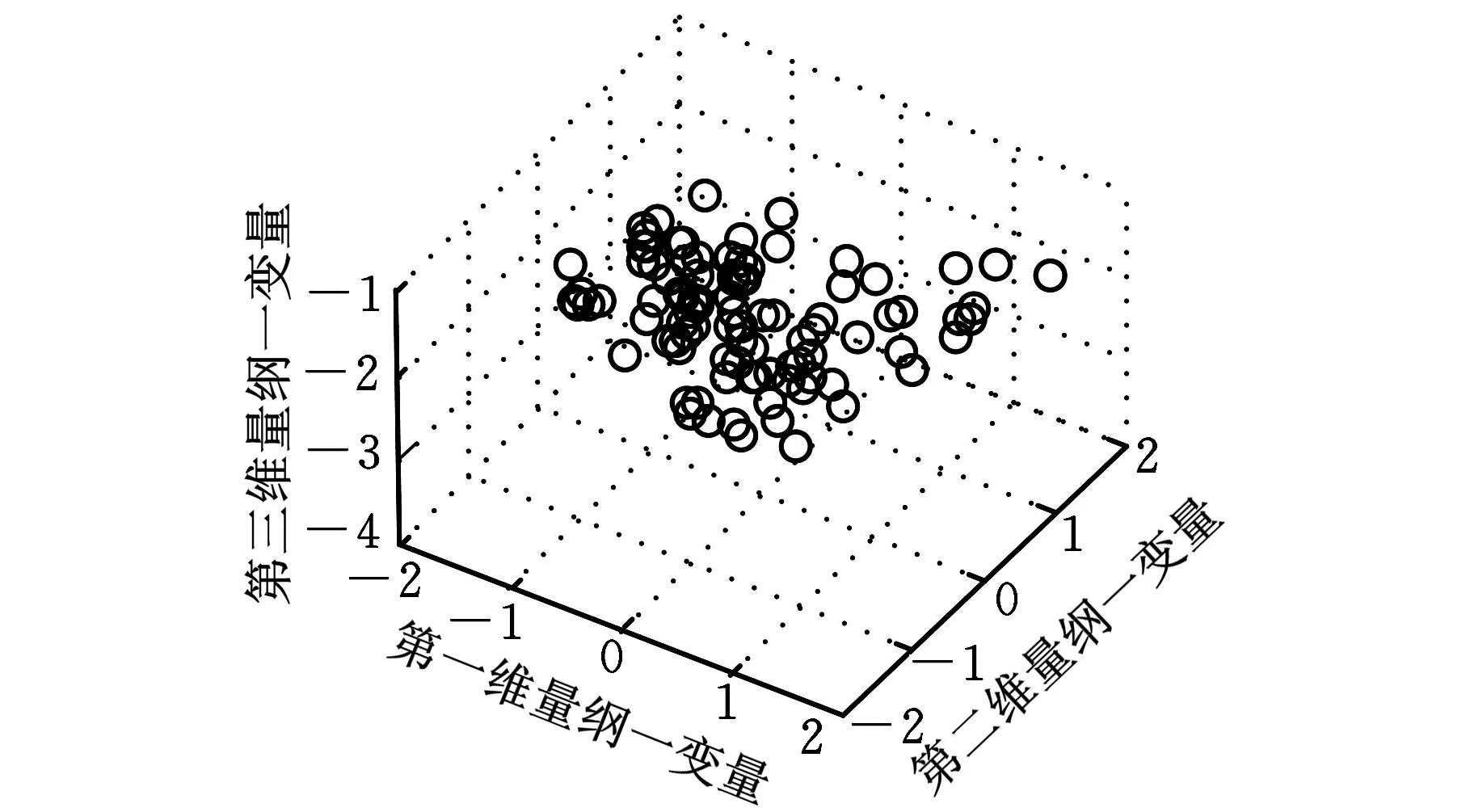
(b)Sonar2 样本三维分布图图4 Sonar数据集的可视化分布图

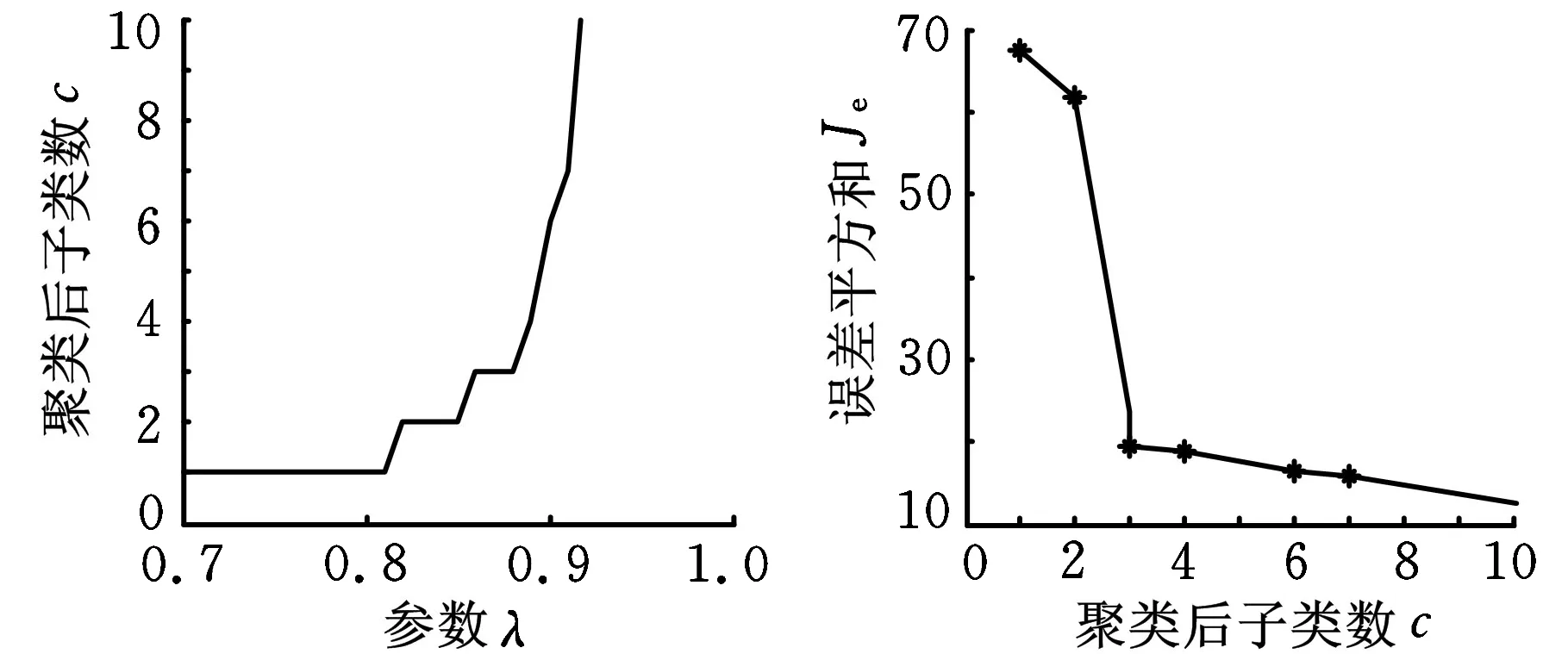
(a)参数λ与子类数关系(b)子类数与误差平方和关系图5 Sonar1聚类的结果

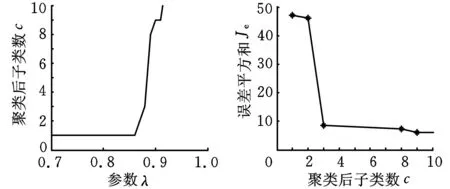
(a)参数λ与子类数关系(b)子类数与误差平方和关系图6 Sonar2聚类的结果

同时采用粒子群优化算法对多超球体一类分类器与单超球体一类分类器两种算法中涉及的惩罚因子C与高斯核参数σ进行参数自适应优化，两种算法在最优参数下得到的识别率如表2所示。

从表2可以看出，Sonar1中多超球体的平均识别率要比单超球体的平均识别率提高了近15%，而Sonar2中两种方法的平均识别率比较接近，这是由于Sonar2的数据聚类特征不是很明显，这与图4b的三维可视图的分布是相符的。对标准数据多超球体一类分类器首先考虑了数据内部的簇分布情况，其对正负类样本的平均识别率总体上与单超球体一类分类器相比均有所提高，可见该算法的有效性。

3.3 转子故障诊断

借助ZT-3多功能转子实验台以及DH5922动态信号测试分析系统，在不同的转速下采集了不平衡、不对中、碰摩以及油膜涡动4类转子故障样本：不平衡25个，不对中22个，碰摩29个，油膜涡动31个。

表2 多超球体一类分类器与单超球体一类分类器对标准数据集的实验结果

本文将实验提取的4类转子故障的样本数据进行频谱分析，得到信号频谱后，对频谱进行归一化处理，然后直接对频谱数据在信息量保持率为95%的情况下进行PCA特征压缩。分别对压缩后的4类特征样本集建立其对应的多超球体一类分类器：不平衡对应所有类别、不对中对应所有类别、碰摩对应所有类别、油膜涡动对应所有类别。建立每个模型时，分别对每一类故障数据随机选取其中2/3的样本数据作为正类训练样本集，将剩余的1/3样本作为正类测试样本集，将其他各故障的1/3样本组合成负类测试样本集，依照本文提出的基于最大树聚类的多超球体一类分类器进行学习。

图7～图10所示为采用最大树聚类法(α均取0.6)，分别对四种转子故障的训练样本集进行聚类的结果。图7b中10个子类以内聚为n个子类与n+1个子类间的误差平方和的差距很小(小于0.001)，因此对于不平衡样本，聚类后的子类个数仍为1。因此根据图7～图10所示聚类后参数λ与子类数c的关系、子类数c与误差平方和Je的关系，分别对每一类故障选择的参数λ以及所得的子类数是：不平衡——0.98，1；不对中——0.99，2；碰摩——0.99，2；油膜涡动——0.98，2。

(a)参数λ与子类数关系(b)子类数与误差平方和关系图7 不平衡样本聚类结果

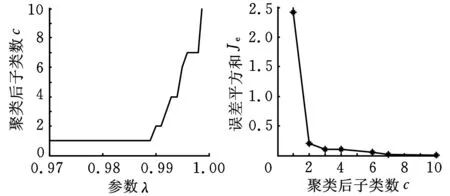
(a)参数λ与子类数关系(b)子类数与误差平方和关系图8 不对中样本聚类结果

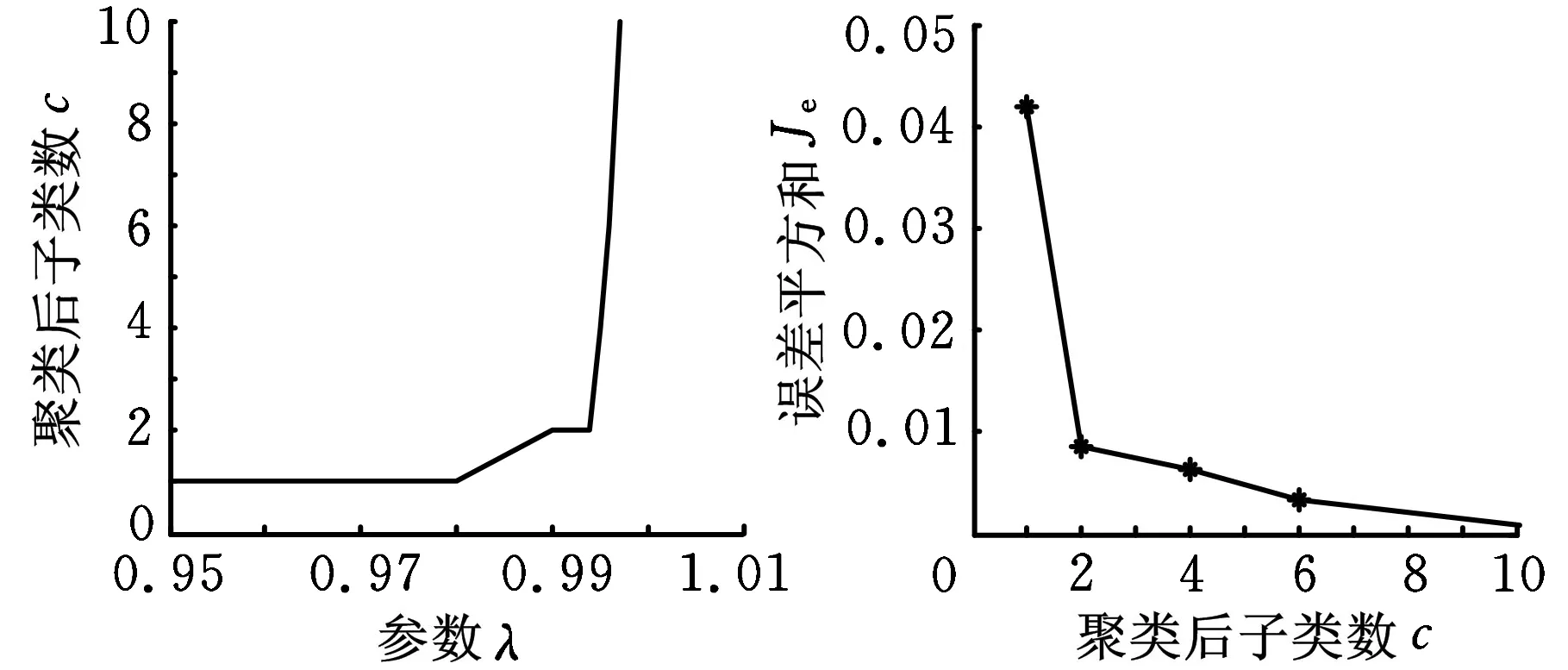
(a)参数λ与子类数关系(b)子类数与误差平方和关系图9 碰摩样本聚类结果

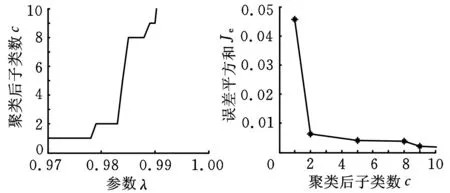
(a)参数λ与子类数关系(b)子类数与误差平方和关系图10 油膜涡动样本聚类结果

根据聚类后的结果采用本文提到的多超球体一类分类器建立模型，同时与常用的单超球体一类分类器比较了实验结果。同样对两种算法均以粒子群优化算法优化各算法中所涉及的惩罚因子C与高斯核参数σ。在最优参数下所得到的识别率如表3所示。从表3的实验结果可知，由于不平衡样本经最大树聚类后仍聚为一个子类，故对于不平衡样本的单超球体一类分类算法即可看成是其多超球体一类分类算法的特例，两者结果一样。其他三类故障样本经聚类后均聚为两个子类：不对中样本采用多超球体一类分类算法不仅支持向量个数比单超球体一类分类法少了，且其对应的识别率也提高了；碰摩样本使用多超球体一类分类法后在支持向量个数增加的情况下，识别率有了提高；油膜涡动样本对应的多超球体一类分类法虽然支持向量个数增加了，但是最后的识别率同样达到了100%。由此可见，该算法相对于常用的单超球体一类分类法在识别率上表现了其有效性。

表3 多超球体一类分类器与单超球体一类分类器对转子故障的识别率

4 结语

本文从考虑数据内在分布的角度出发研究了一种基于最大树聚类的多超球体一类分类算法。首先对经PCA特征降维后的训练样本集采用最大树聚类算法实现聚类,得到对应的内在分布簇形成的各子类；然后对各簇子类分别进行一类支持向量机分类器训练，并且利用粒子群优化算法获取最优参数，得到各子类对应的超球体；最后建立由各子类对应的超球体而形成的多超球体一类分类模型。分别将该方法应用于仿真数据、UCI标准数据集以及转子故障数据这三个实例中，实验结果表明，当样本数据呈簇类分布时，尤其是聚类特征比较明显时，该方法相对于常用的单超球体一类分类方法具有可行性及有效性。

[1] Juszczak P. Learning to Recognise:a Study on One-class Classification and Active Learning[D]. Delft: Delft University of Technology, 2006.

[2] Camci F, Chinnam R B. General Support Vector Representation Machine for One-class Classification of Non-stationary Classes[J]. Pattern Recognition,2008, 41: 3021-3034.

[3] Tsang I W,James T K,Li S.Learning the Kernel in Mahalanobis One-class Support Vector Machines[C]//Proceeding of the International Joint Conference on Neural Networks.Vancouver,Canada,2006:1169-1175.

[4] Tax D. One-class Classification: Concept-learning in the Absence of Counter-examples[D].Delft: Delft University of Technology,2001.

[5] 谭真臻, 陈果, 孙丽萍. 基于Hilbert谱图特征的航空发动机转子故障智能诊断[J].机械科学与技术,2010, 29(9):1177-1181.

[6] 冯爱民,陈松灿. 基于核的单类分类器研究[J].南京师范大学学报(工程技术版),2008,8(4):1-6.

[7] 戴蒙,林家骏,刘云翔.基于FCM聚类的多超球体一类分类数字图像隐藏信息[J].中国图像图形学报,2008,13(10):1918-1921.

[8] Wang D, Yeung D S, Tsang E C C. Structured One-class Classification[J].IEEE Trans. on Systems, Man, and Cybernetics-Part B:Cybernetics,2006,36(6):1283-1294.

[9] 肖健华. 智能模式识别方法[M]. 广州: 华南理工大学出版社, 2006.

[10] 杨梦宁,杨丹,张强劲.基于最大树法的模糊图像分割方法[J].计算机科学,2005,32(8):190-191.

[11] Duda R O,Hart P E,Stork D G.模式分类[M].李宏东,姚天翔,等,译.2版.北京：机械工业出版社，2003.

[12] Chapelle O, Vapnik V, Bousquet O, et al. Choosing Multiple Parameters for Support Vector Machines[J]. Machine Learning,2002,46(1):131-159.

[13] 王东,吴湘滨.利用粒子群算法优化SVM分类器的超参数[J].计算机应用,2008,28(1):134-135.

[14] 邵信光,杨慧中,陈刚.基于粒子群优化算法的支持向量机参数选择及其应用[J].控制理论与应用,2006,23(5):740-743.