地铁列车牵引计算的研究

林 青

（西南交通大学 信息科学与技术学院，成都 610031）

城市轨道交通是城市公共交通客运系统的骨干，是以大众化、大运量、大站距为特点的安全、舒适、快速、准时的绿色交通工具，是采用独立的专用轨道、高密度运行的、为中长运距服务的、现代化的城市客运快速骨干系统，通常是指服务于城市内部为主和适当外延的线路。对城市轨道交通车辆运行过程进行实时仿真模拟可以更好地满足运输需求。准确、快速地计算出列车在各种不同条件下的运行效果并予以评价是牵引计算的任务。

1 城市轨道交通的特点

城市轨道交通与大铁路在诸多方面有很大不同，主要表现在：紧急制动距离很短；区间长度比较短，类似公共汽车的站间距；在运行中存在频繁的启动和制动过程；线路条件苛刻，曲线半径有时甚至小于250 m，坡度有时很大（很小），甚至超过4 %；操纵要求非常严格，启动和制动过程要求快速、平稳，停站要求非常准确，舒适度要求较高等。

2 CBTC安全制动模型

IEEE1474.1关于CBTC系统推荐的典型的安全制动模型如图1。

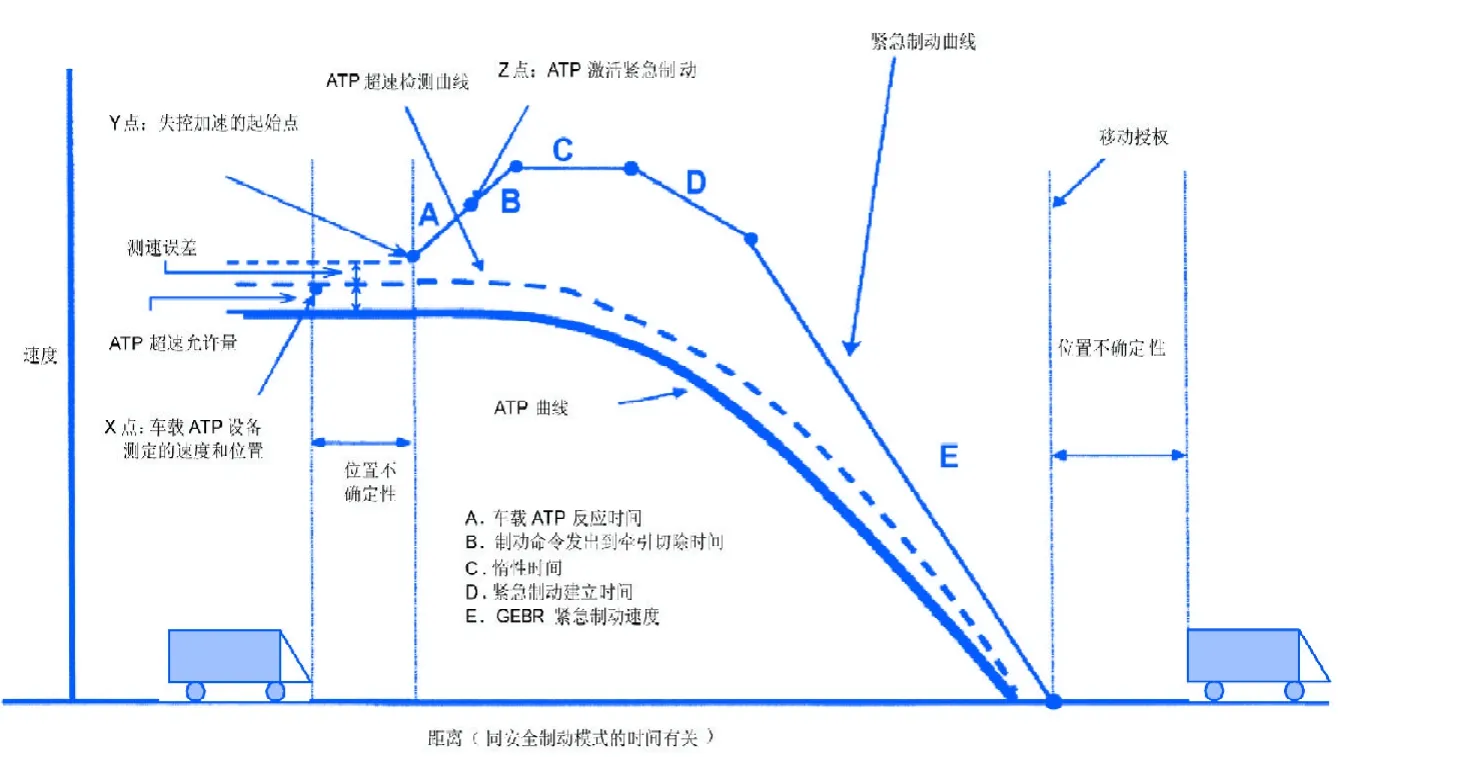
图1 CBTC系统安全制动模型

图中紧急制动曲线表示的是在最不利情况下的开环速度-距离曲线。一旦施加紧急制动，列车将遵循该曲线运行制动列车停止。紧急制动曲线必须保持等于或小于安全速度曲线，若超过安全速度曲线，就会出现严重的危险（脱轨或撞车）。

图中的ATP超速检测曲线就是本文以后将会提到的紧急制动触发曲线，指如果ATP子系统一旦发现列车在某检测点的测量速度超过该曲线，就会立即触发紧急制动程序的速度-距离曲线。激活紧急制动后，ATP子系统就脱离原来的控制，列车按照（或者低于）紧急制动曲线进行紧急制动。紧急制动曲线包括一个失控牵引阶段，这个阶段直到牵引完全取消为止。ATP曲线是指低于ATP超速检测曲线一个超速容限的速度-距离曲线。它是ATP子系统所使用的基本曲线。

3 建模

本文在上述IEEE1474.1关于CBTC系统推荐的典型的安全制动模型的基础上，建立了如下的列车制动模型，如图2。

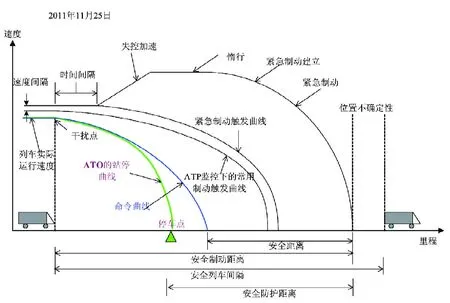
图2 列车制动模型

列车制动模型的计算：EB包络线的计算，紧急制动触发曲线（EB触发曲线）的计算，全常用制动触发曲线（FSB曲线）的计算，列车命令速度曲线的计算，实际运行速度曲线的计算。

4 牵引计算

4.1 EB包络线的计算

根据IEEE1474.1标准安全制动模型绘制的列车制动模型，EB包络线由列车失控加速曲线、列车惰行曲线、列车紧急制动曲线构成。

EB包络线中列车失控加速曲线是列车制动时，由于某些原因，列车没有制动反而以更大的加速度前冲的过程。失控加速完成时，列车的速度达到最大值。按列车运行方向计算时，列车的失控加速度按列车失控加速前的速度来选取；按列车运行反方向计算时，列车的失控加速度按列车失控加速后的速度来选取，且取为反向的失控加速度。

EB包络线中列车惰行曲线是列车停止失控加速到开始制动的过程，列车保持一段时间的惰行状态，惰行完成后，列车进入紧急制动状态。按列车运行方向计算时，列车的惰行加速度按列车惰行前的速度来选取；按列车运行反方向计算时，列车的惰行加速度按列车惰行后的速度来选取，且取为反向的惰行加速度。

EB包络线中列车紧急制动曲线：列车在失控加速、惰行后进入紧急制动状态，直到列车完全停止运行。列车的紧急制动减速度由用户设定。

EB包络线的绘制通常采用反向绘制的方法。EB包络线的反向绘制是由安全停车点开始，倒推列车的紧急制动曲线，惰行曲线，失控加速曲线，是一次绘制而成的。安全停车点可以由用户设定。

4.2 EB触发曲线的计算

EB触发曲线的计算是在包络线计算的基础之上进行的，必须先进行包络线的计算，才能进行EB触发曲线的计算。

EB触发曲线与包络线的关系：EB触发曲线是由EB包络线反向推导而成，EB包络线的离散化后的（V-S）点通过列车惰行、失控加速的反向运算，推出EB触发曲线的离散化（V-S）点，然后连续化成为列车的EB触发曲线。

EB包络线的离散化：EB包络线是一条连续的曲线，为了计算EB触发曲线，必须将其离散化，本系统采用位移的离散化，离散的间隔由用户设置，一般取为10 cm～100 cm。

EB包络线离散点推EB触发曲线离散点：从EB包络线离散点推导出惰行前的（V-S）点，简称中间点。从中间点推导出失控加速前的（V-S）点，此即EB触发曲线离散点。

4.3 FSB触发曲线的计算

FSB触发曲线（列车常用全制动触发曲线）又称ATP Supervised Service Brake Profile（ATP监控的常用制动曲线），FSB触发曲线由EB触发曲线推导。

FSB触发曲线的性质：全常用制动速度是非安全监控速度曲线，当列车速度触及常用制动触发曲线时，车载控制器将施加全常用制动；列车速度系统引用全常用制动触发速度的目的是为了提高系统的可用性，避免系统频繁发生紧急制动；与紧急制动的区别是当列车速度降低到正常范围之内后，全常用制动的制动命令解除，列车无需完全停止。

FSB触发曲线与EB触发曲线的间隔为当前速度下的时间间隔Teb-fsb和速度间隔Veb-fsb；本系统中Teb-fsb和Veb-fsb均为用户可设，Teb-fsb默认值为3.0 s，Veb-fsb默认值为2.5 km/h。

FSB触发曲线的计算步骤：

（1）对EB触发曲线实行离散化，本系统采用位移的离散化，离散的间隔由用户设置，一般取为10 cm～100 cm；

（2）取紧急制动触发曲线上的离散点（Xeb,Veb）；

（3）计算当前速度下的FSB触发点位置：

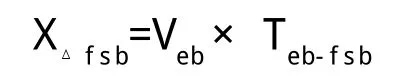
（4）计算全常用制动触发点速度：

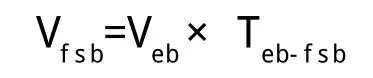
（5）得到对应的FSB触发点：(Xfsb,Vfsb)

当紧急制动触发曲线用函数表达：

Vebtrigger=f(s)

全常用制动触发曲线可用函数表示为：

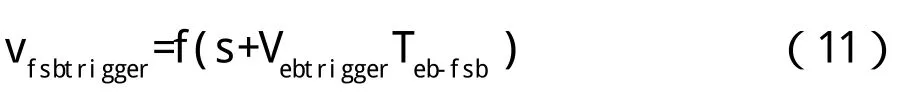
为了保证全常用制动触发曲线上的任何一点的瞬时制动率都小于全常用制动率，用Teb-fsb（s）替代公式（11）中的Teb-fsb，并且：

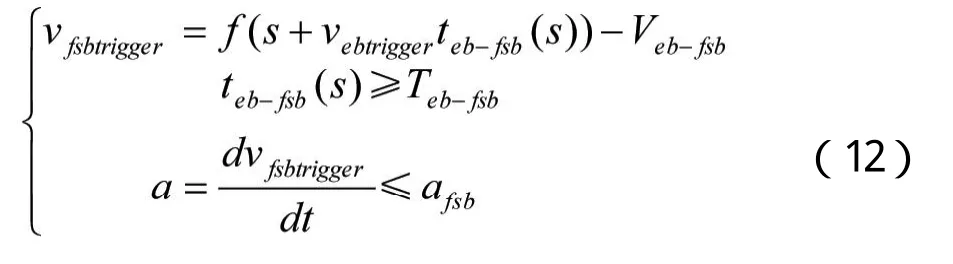
其中afsb为全常用制动率。

4.4 命令曲线的计算

基于同样的算法，命令速度曲线与全常用制动触发曲线的间隔为当前速度下的时间间隔Tfsb-ato和速度间隔Vfsb-ato，本系统中取Tfsb-ato为3.0 s，Vfsb-ato为2.5 km/h。

上式描述了列车采用ATO可变制动率点的停车方式（ATO variable brake rate），但列车在功能停车点（车站停车点或折返停车点）停车时，命令速度采用恒定制动率：

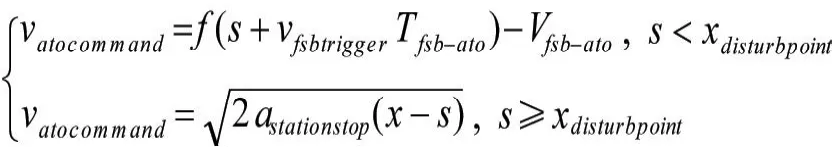
其中，x为车站停车点，astationstop为列车停站的恒定制动率，xdisturbpoint为停站初始点，即列车开始按照恒定的停站制动率进站停车的位置。

4.5 实际速度曲线

列车按照命令速度曲线行驶，形成列车实际速度曲线。与命令速度曲线基于同样的算法。

4.6 仿真结果

以成都地铁1号线为例，对该模型进行仿真验证，得到的结果如图3。

图3 成都地铁1号线仿真结果

5 结束语

列车的牵引计算过程是一个很复杂的过程，这是由于在实际运行过程中可以有不同的机车、不同的牵引曲线、不同的线路坡度组合。因此，本文根据一定的牵引原则，利用计算机对列车的牵引计算进行了模拟研究，较好地实现了在整个列车运行过程中牵引过程的模拟。

[1]谢小淞. 城市轨道交通列车牵引计算系统的研究[J]. 交通运输工程学报. 2005，5（4）：20-26.

[2]钮泽全. 牵引计算学[M]. 北京：中国铁道出版社，1984.