基于排队论的应急物资装载模型研究

李 聪，李建国

（兰州交通大学，机电技术研究所，兰州 730070）

目前，国内对应急物流装运车辆方面的研究主要有车辆的调配、物资运输的路径设计、车辆运输路径优化等，对排队论在应急物流方面的研究较少。应急物流是指以提供重大自然灾害、突发性公共卫生事件及公共安全事件等突发性事件所需应急物资为目的，以追求时间效益最大化和灾害损失最小化为目标的特种物流活动。本文以应急物流中的车辆到达、装运等在应急物流活动中耗时较大的环节为研究对象，采用排队论思想重点考察车辆到达应急物流中心耗时和等待应急物资装载耗时，以期得到应急物流中车辆装运配送的理论指导方法。

1 应急物资装载GI/M/1模型建立

1.1 模型建立条件和参数符号说明

本文研究的是单个应急物流中心运送救灾物资到单个救援点的模型。模型建立有以下假设：

（1）到达时间分布：车辆到达应急物流中心的时间服从正态分布，即服从N～（ηε3）。

（2）服务机构：应急物资装载服务台有1台。

（3）服务规则：首先到达应急物流中心车辆首先安排应急物资装载，即遵循先到先服务原则。

（4）服务分布时间：应急物流中心应急物资服务台的服务时间服从参数为η负指数分布。

（5）车辆到达应急物流中心的间隔时间之间相互独立，车辆到达应急物流中心间隔时间与应急物资装载服务时间相互独立。

根据上述的假设，建立应急物资装运GI/M/1模型。

1.2 排队论应急物资车辆装运模型建立[1]

设Vn+1为第n个车辆与第n+1个车辆到达应急物流中心的间隔时间内，服务台装载服务完的车辆数，则：

这样，在应急物流中心第n个车辆到第n+1个车辆的间隔时间内，系统从状态i转移到状态j，按全概率公式转移概率为：

由排队论可知，当λ/μ<1时，到达应急物流中心车辆的队长平稳分布。此平稳方程记作{P－n}。

其中，σ为待定常量。

把（4）式带入（3）式，得：

把（2）式代入（6）式，得：

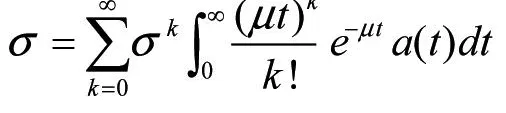
其中，A*(s)是a（t）的拉普拉斯变换。

车辆到达应急物流中心的时间间隔服从正态分布：

将（8）式代入（7）式，得：

解得，

等待装载应急物资的车辆的等待时间分布函数为：

等待装载应急物资的车辆平均等待时间为：

2 理论计算与仿真分析

2.1 理论计算

应急运输车辆到达应急物流中心时间服从正态分布，假设其期望η=4 ，标准差ε=3。

应急物流中心的服务台服务时间，即应急物资装载时间为负指数分布，假设其参数μ=3。

由（10）式可知，σ=0.63。

根据式（12）式和（14）式，得等待装载应急物资的车辆，其平均等待队长为：

等待装载应急物资的车辆平均等待时间为：

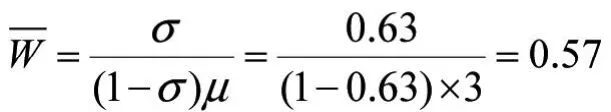
2.2 仿真分析

同样参数情况下，利用ExtendSim仿真软件对等待装载应急物资的车辆，其平均等待时间和平均等待队长进行仿真，先建立一个单到单的服务模型见文献[2]。取仿真时间为1 440 min。同样的假设，应急运输车辆到达应急物流中心的分布为正态分布N ～ (4,9)。应急物资装载服务取服务时间服从负指数分布且参数取值为3，时间单位都为min。取其中一次的部分参数如表1。

表1 仿真数据

由此可知，等待装载应急物资的车辆的总队长为：

等待装载应急物资的车辆平均等待时间为：

等待装载应急物资的车辆平均等待队长为：

因此，对比理论分析结果和本次仿真的结果可知，理论计算与仿真数据差异不大，在此参数条件下，可以满足应急处置要求。仿真结果可为考虑实际应急物资运送时救灾能力是否足够提供有效的依据。若仿真数据和理论计算之间差异较大，即当应急中心等待装载应急物资的车辆，其平均等待时间和平均等待队长过长时，应考虑重新配置救灾力量。如果等待装载应急物资的车辆，其平均等待时间过短或者平均等待队长过短，几乎没等待时间或等待队长，表明可能是服务台过多、车辆过少，根据应急处置具体情况决定应减少服务台或者增加装载运输的车辆。

3 结束语

由于应急物流具有很大的不确定性，车辆配送问题模型的结构与算法选择会有较大的不同。采用仿真方法可以最大限度地模拟实际应急物流活动发生的情况。本文从车辆装运配送理论的角度对等待装载应急物资的车辆进行了研究，推导计算并仿真了等待装载应急物资的车辆的平均等待时间及平均等待队长。为实际情况下决策者考虑是否应增减服务台和增减应急救灾车辆提供了有效的依据。

[1]孟玉珂. 排队论基础及应用[M]. 上海：同济大学出版社，1989.

[2]秦天保，王岩峰.面向应用的仿真建模与分析-使用ExtendSim[M]. 北京：清华大学出版社，2009.