基于Simulink的LDPC码仿真研究
王卫华,樊红莉
(湖北汽车工业学院 电气与信息工程学院,湖北十堰442002)
1962年Gallager首次提出了LDPC(Low Density Parity Check)码[1],这是一种具有稀疏校验矩阵的分组码,其性能非常接近Shannon极限[2],具有超强的纠错抗干扰能力。由于其良好特性,LDPC码成为差错编码领域里的研究热点。IEEE802.lln[3],IEEE802.l6e[4],DVB-T2[5],CMMB(China Mobile Multimedia Broadcasting)[6],CDTTB(Chinese Digital Terrestrial Television Broadcasting)[7]等众多标准都开始采用LDPC码作为信道编码方案。
LDPC码离广泛应用有一定的差距,阻碍其发展的难点在于校验矩阵的设计。上述的诸多标准没有校验矩阵的构造思路,仅仅只有校验矩阵的具体数值,对LDPC码的发展非常不利。文献[8-10]介绍的几种LDPC编码构造方法都能使校验矩阵具有满秩特点,但是都有较多缺点,比如LDPC码的高斯消元法编码,计算复杂度较高,并且变换后的矩阵不具有稀疏特性;基于近似下三角矩阵的有效编码方法,也是要经过非常复杂的矩阵处理,不利于构造超长码长的LDPC好码;构造半随机校验矩阵的编码方法,虽然方法简单,也利于硬件实现,但是存在列重为1的列,这对迭代译码过程非常不利,有可能会产生误码平台;至于具有循环码特性的LDPC码的编码方法,其构成的通信系统性能远低于随机构造的系统性能。鉴于此,本文在Gal-lager的构造方法[1]基础上提出了一种新的具有满秩特点的校验矩阵构造方法。
1 LDPC码的校验矩阵构造方法
LDPC码是线性分组码的一员,它的名字来源于具有稀疏特点的校验矩阵,即校验矩阵中仅有少量的1,大部分位置上为0,如图1所示。

图1 LDPC码的校验矩阵
Galager最早给出了LDPC码的定义,它的校验矩阵H满足下面3个条件[1]∶1)H的每行有ρ个“1”;2)H的每列有λ个“1”,λ≥3;3)与码长m和H矩阵的行数w相比,ρ和λ都很小。
通常用F(m,dz,ds)来表示LDPC码,m代表该码的长度。编码中的所有比特位数均参与检验dz个校验等式,而每个校验等式均有ds个不同的比特位包含的码字组成。其中的校验等式数为

编码效率为

式(2)成立条件为校验矩阵是满秩矩阵。
根据线性分组码的特性,域V中m×k维的P能由(m-k)×m维的校验矩阵H表示:
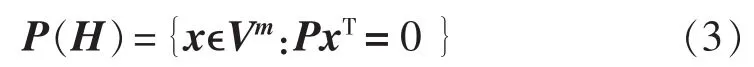
Gallager利用简单的矩阵任意置换和重联来构成校验矩阵,即由固定的方法构造规则矩阵(比如单位矩阵),将该矩阵的全部列做任意的排列和组合,形成一系列新的规则矩阵,最后由这些规则子矩阵联合成所需要的校验矩阵。校验矩阵H的样式如式(4)所示。
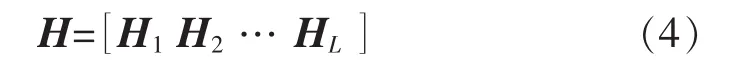
2 满秩的校验矩阵算法描述
1)初始化矩阵H的行列常数n和k;
2)生成一个(n-k)行和n列的矩阵,并初始化值为全零;
3)使每列随机产生3个1;即列重为3;
4)求出每行1的最多个数,即行重的最大值;
5)尝试在列上分散1的位置,使行重分布尽量均匀;如果某行行重大于行重的最大值,则进行随机选择某一该行上为1的列来处理,将改行上的1分散到其他行上;
6)尝试消除4环,尽量使每2列之间重叠‘1’的个数不大于1;这样构造的矩阵由于每2列之间重叠“1”的个数不大于1;
网络文学变现方式多样化,尤其是优质网络文学作品,主要通过创新性和趣味性满足受众的心理需求,持续关注和讨论即可实现内容变现。如盛大文学拥有的内容资源,它的变现方式分为以下几种。
7)假定 i初始值等于(n-k+1);如果 i等于(n+1),则退出程序;
8)依次判断矩阵H2的主对角线上的值是否为1;如果等于1,程序直接跳到第11)步;
9)如果不等于1,进行以下操作:循环扫描该值y(假设该行参数为k1)对应列下面的所有元素,遇到1停止,记录此时对应的行数为k2;如果扫描到最后一行都没有碰到1,则将y强行赋1,同时i自动加1,然后转到第7)步;
10)交换H矩阵中k1和k2的所有值;
11)i=i+1,转到第7)步。
算法中的核心部分是构造校验矩阵H中的H2,使方阵的对角线全部变换成1,也就是第7)步到第11)步,该算法在MATLAB中运行效果良好,生成的校验矩阵H绝大部分满足满秩条件。基于这个原因,每生成一个矩阵,必须利用Simulink提供的“fec.ldpcenc”函数进行判断,如果判断出子矩阵不可逆,必须重新运行上面的程序,随机生成新的校验矩阵,直到生成的矩阵满足子矩阵可逆条件为止。经过大量的实验证明,计算机重复寻找的次数不会超过10次。
3 仿真模型及性能分析
为了验证新的算法构造出的LDPC码性能,根据数字通信系统的基本工作原理,构造出图2的LDPC编解码系统仿真模型。

图2 LDPC编解码系统仿真模型
图2中的信源为二进制数据比特流,经过LDPC纠错编码和调制映射后通过AWGN信道;接收端进行调制映射和LDPC译码,信宿输出二进制比特流。其中的误码率检测模块对该系统进行误码率统计。对应的Simulink仿真系统如图3所示。

图3 LDPC系统Simulink仿真图
3.1 不同校验矩阵构造方法对应的LDPC系统性能
为了比较新校验矩阵构造方法和Galager校验矩阵构造方法对应的LDPC码性能,利用Galager的方法构造了码率为1/2,码长为2000的LDPC码。图4是两者比较的性能仿真图形。从图4中可以看出,新的校验矩阵构造出的LDPC码系统性能优于Galager构造的LDPC码系统性能。如SNR等于1.6dB情况下,本文提出的新的校验矩阵构造的LDPC码系统BER比Galager随机构造的LDPC码系统BER下降约0.6dB。
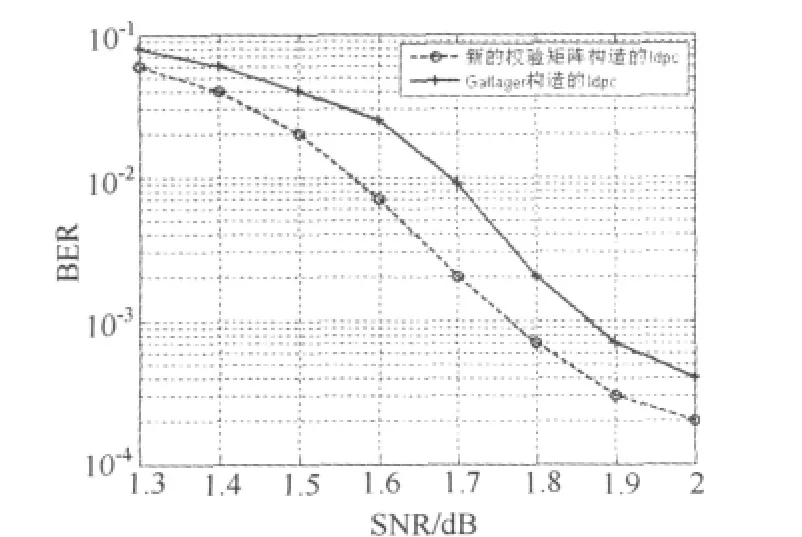
图4 不同校验矩阵对应的LDPC系统仿真图形
3.2 不同码长对应的LDPC系统性能
研究不同码长的LDPC码对系统性能的影响。图5是在码率为1/2的情况下,码长分别为500、1000和2000时系统性能的仿真结果,可以看出,在信道信噪比相同的情况下,随着LDPC码长的增长,系统的BER越来越小。如SNR为1.8dB时,码长为2000的LDPC码较码长为1000的LDPC码的性能要好大约1dB,而码长为2000的LDPC码较码长为500的LDPC码的性能要好大约1.5dB。
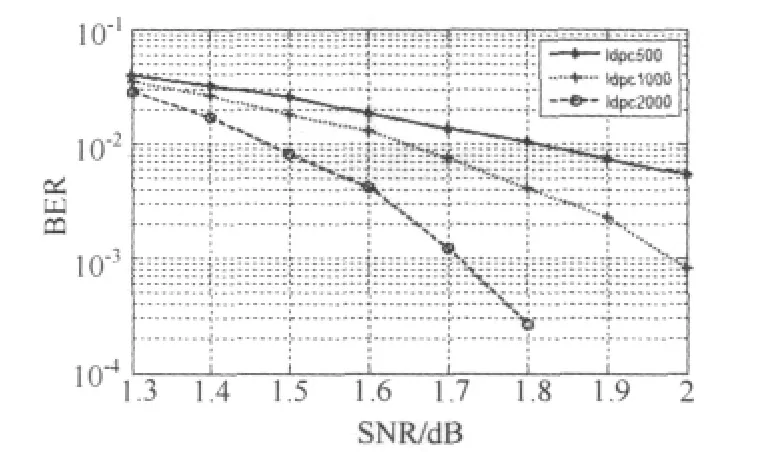
图5 不同码长的系统性能曲线
3.3 不同码率对应的LDPC系统性能
对于LDPC码来说,码率等于信息位与码长的比值。码率越低,说明有用的信息比特越少,同时用于校验的比特越多。
图6给出了码长为2000时采用不同码率的系统性能曲线。从图6中可以看出,在SNR等于1.5dB时,码率为1/2的LDPC码较码率为3/4的LDPC码的性能要好大约1.1dB。
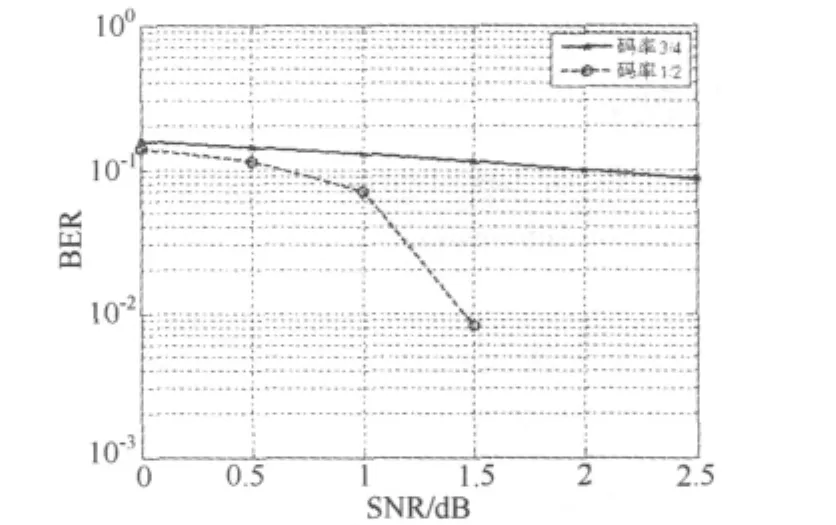
图6 不同码率的系统性能曲线
3.4 不同迭代次数对应的LDPC系统性能
LDPC译码采用了外信息传递的处理方法,通过迭代,后一步可以充分利用上一步得到的外信息来不断提高译码的可靠性。随着迭代次数的增加,译码性能会越来越好。
图7是码长为2000的LDPC码在不同迭代次数下的译码性能曲线,它清楚地反映了迭代次数对译码性能的影响。如SNR等于1.8dB情况下,迭代10次时的BER比迭代20次后的BER接近下降了约0.6dB;而迭代30次较迭代10次时的BER下降了1.2dB。
4 结 论
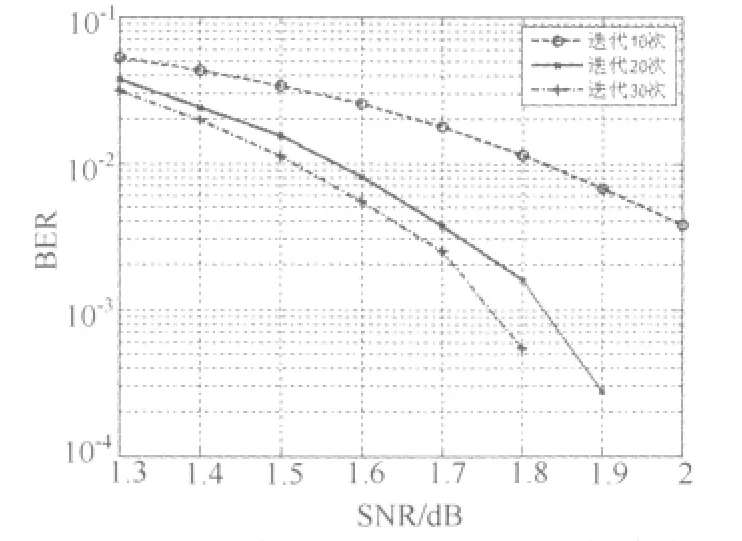
图7 不同迭代次数对应的系统性能曲线
本文提出了一种新的具有满秩特点的校验矩阵构造算法,结合Simulink进行了系统级仿真,对不同的校验矩阵、码长、码率、迭代次数对应的LDPC编码分别进行分析,证明了该算法的科学性。通过对比表明,新的校验矩阵构造出的LDPC码系统性能优于Galager构造的LDPC码系统性能;LDPC码的误码性能短码劣于长码;LDPC码的码率越高性能越低;LDPC译码增加迭代次数后性能提升。该算法对应用越来越广泛的LDPC编码技术研究有一定的参考价值。
[1]Gallager.R.G.Low-Density Parity-Check Codes[D].IRE Trans on Information Theory,1962,8(3):208-220.
[2]D.J.MacKay,R.M.Neal.Near Shannon limit performance of lowdensity Paritycheck codes[J].IEEE Transactions on Communications letters,1996,32(8):1645-1646.
[3]Draft Standard for local and metropolitan area networks– specific requirements– Part 11∶Wireless LAN Medium Access Control(MAC)and Physical Layer(PHY)specifications[S].IEEE P802.ll/D2.00,February 2007.
[4]IEEE Standard for LAN/MAN part16∶Air Interface for Fixed and Mobile Broadband Wireless Access Systems[S].IEEE Std 802.16e-2005 and IEEE Std 802.16-2004/Cor 1-2005(Amendment and Corrigendum to IEEE Std 802.16-2004),February 2006.
[5]Draft ETSI EN 302 755 Vl.1.1(2008-04).frame structure channele coding and modulation for a second generation digital terrestrial television broadcasting system(DVB-T2)[S].
[6]GY/T 220.1-2006,CMMB广播信道帧结构、信道编码和调制[S].
[7]GB20600-2006,数字电视地面广播传输系统帧结构、信道编码和调制[S].
[8]T.J.Richardson,R.Urbanke.Efficient encoding of low density parity check codes[J].IEEE Trans On Inform Theory,2001,47(2):638-656.
[9]Y.Kou,S.Lin,M.Fossorier.Low Density Parity-Check Codes Based on Finite Geometries:A Rediscovery and New Results[J].IEEE Trans On Inform Theory,2001,47(11):2711-2736.
[10]Kamiya N.Efficiently encodable irregular QC-LDPC codes constructed from self-reciprocal generator polynomials of MDS codes[J].IEEE Communications Letters,2010,14(9)∶8660-862.

