飞轮在轨扰动问题地面试验验证

付国庆 ，姜 健

（1. 上海交通大学 机械与动力工程学院；2. 上海卫星装备研究所：上海 200240）

0 引言

飞轮作为卫星姿控系统中的主要执行机构，是高精度卫星的主要干扰源之一。飞轮在高速旋转过程中所产生的高频颤动和局部耦合的低频扰动对卫星的稳定与姿控精度产生不利影响。由于扰动中存在较多的非线性因素，所以单纯的理论分析或数值仿真无法有效针对扰动问题提出解决方案[1]，需要进行有关地面试验验证。

“风云三号”气象卫星在轨运行过程中，发现服务舱的第Ⅲ象限基准A与第Ⅱ象限基准B两个飞轮同时工作时，卫星结构板局部扰动响应较大。根据遥测数据结合地面仿真和试验验证测试结果分析还发现：飞轮在某些转速下，结构板上除有高频颤动外，还会在特定部位产生强烈的低频振动，进而引起整体结构上的较大振动响应。这种耦合振动必然对卫星本体结构件及其他星上设备的可靠性产生影响。

为了避免后续型号产生同样问题，针对“风云三号”（02星）飞轮开展了地面验证试验，同时采取数值仿真与试验手段相结合的方式验证了改进措施的有效性，以避免飞轮与结构本体发生振动耦合。

1 飞轮在轨扰动问题分析

一般来讲，转动部件的固有频率或临界频率是由转子的质量和刚度以及支承结构来决定的。对“风云三号”卫星所采用飞轮的扰动进行分析，根据扰动源不同，其扰动原因主要有以下5方面。

1）飞轮转子不平衡

转子不平衡分为静不平衡和动不平衡两种情况。静不平衡是由于质量分布不均所造成的实际转子质心偏离几何中心或惯性轴中心而产生，而动不平衡是由于转子惯性轴和实际旋转轴不重合所导致。当飞轮工作时，由不平衡而引起的力和力矩将直接作用于高速转子，使其产生一定的自激振动，进而对卫星的正常工作造成不利影响。而飞轮不平衡的原因直接与其加工制造精度密切相关。

2）飞轮结构挠性

飞轮结构具有一定的挠性，可能与转子不平衡引起的高频激励产生谐振，从而出现结构弹性振动。如果由不平衡特性而引起的高频激励频率接近飞轮的固有频率，则会产生共振现象，使卫星的稳定度和姿态控制精度受到更加严重的影响。因此，在飞轮设计时，通常会让飞轮的固有频率远离转子旋转速度上限。尽管如此，在实际运行中仍会存在不同程度的结构振动现象[2]。

3）安装刚度与轴承振动特性

目前星上的姿控飞轮主要采用机械支承。对于大质量飞轮加小刚性支架构成的系统，由于安装支架刚度较弱，飞轮转速变化而产生的自激振动模态会通过支架传递给其他有效载荷。另外，滚动轴承是传递其他振动的中间环节，再加上它本身的动态特性，在转子的旋转过程中必然会诱发出具有多种高频成分的复杂振动。系统实际输出的控制力矩除电动机驱动力矩外还包含轴承的摩擦力矩。当反作用轮工作并且其转速过零时，往往会出现转速变化滞后和轴承摩擦力矩抖动的现象，从而使飞轮产生扰动。轴承润滑及其摩擦特性所引起的低速摩擦扰动是目前控制系统设计时所要考虑的主要扰动因素之一[3]。

4）电动机输出转矩特性

转矩特性是电动机重要的性能指标，其中包括平均转矩和转矩的平稳性。飞轮一般采用永磁无刷直流电动机。由于这种电动机的结构特点，使得其平均转矩比其他类型的电动机高，但是转矩的平稳性不如其他电动机。这会对飞轮控制力矩的准确输出产生一定程度的干扰，并导致飞轮产生高频扰动。此外，电动机在反作用轮正反转过零时容易出现低频振荡，影响控制力矩的输出，对卫星稳定和姿态控制产生影响[3]。

5）其他转动部件的振动耦合

飞轮执行姿轨控时，往往需要多个运动机构协同工作，如步进机构、消旋组件机构和其他运动机构，这些都是自激振动源。多重振动叠加所引发的复杂频段的扰动与星体支撑结构板的固有频率相耦合，对星上设备构成不利影响。

2 问题解决方案

经过数值仿真分析，我们把研究重点放在改变系统频率、增加阻尼以降低响应量级的方向上，主要措施是安装局部吸振器或进行局部刚度加强。

选用4个进口飞轮（分别标为1号、2号、3号和4号）进行改进方案的研究，主要内容包括：

第一步为初步优选，对飞轮进行了3种状态的振动测试。

1）飞轮及支架柔性悬吊状态扰动测试（以下简称悬吊试验）；

2）飞轮及支架刚性固定状态模态及振动测试（以下简称刚性固定试验）；

3）飞轮及支架安装在星上振动测试（简称星上状态试验），掌握各个飞轮的扰动形式和扰动量级。

第二步为有效性试验，即根据第一步得到的试验数据，挑选两个扰动剧烈的飞轮在初样星上进行以下3项减振方案的有效性验证试验。

1）进行局部结构加强，提高响应频率以避开共振耦合频率；

2）安装等效于两个振子的串联吸振器；

3）在飞轮支架上附加纵向约束阻尼支杆。

第三步，对上述试验的工作、试验数据及分析结果进行对比分析，得出优化的改进方案。

3 星上单飞轮特性摸底试验

本试验目的是获取飞轮工作时所引起的星上振动量级和固有频率，筛选出 2个扰动较大的飞轮，分别安装在初样星服务舱的第Ⅲ象限基准 A和第Ⅱ象限基准 B的位置上，并加装侧板。先后对这两个飞轮进行试验，给定工况是控制飞轮从3 000 r/min持续加速到6 000 r/min左右，记录各传感器的响应。

3.1 未加刚性过渡板条件下的飞轮测试结果

服务舱的第Ⅱ象限基准 B位置处飞轮的加速度测试传感器布置如图1所示（1#、2#、3#传感器在支架上，4#在轮缘上，5#、6#、7#分布在支撑板上，其中5#靠近中心承力筒和隔板）。

图1 服务舱第II象限基准B飞轮的测点布置Fig. 1 Measurement point layout of B flywheel on the left upper quadrant of service module

将飞轮转速从3 000 r/min提高到6 000 r/min，1#传感器的3个方向时域响应和FFT平均谱如图2所示，其中红色为x方向的响应，绿色为y方向的，蓝色为z方向的，以下各图（有定义的除外）的颜色定义相同。

对时域响应的最大峰值处进行频谱分析，得到的频率为94.5 Hz，其对应转速为5 670 r/min。由于飞轮的工作转速一般为5 400±200 r/min，因此该频率引发大量级共振的可能性很高。当转速为5 670 r/min时，飞轮转轴附近x、y、z方向的振动响应幅值分别为1.3 g、0.8 g、0.5 g。

图2 1#传感器在x、y、z三个方向的加速度响应Fig. 2 Acceleration responses in x, y, z directions for sensor 1#

结构板上的振动响应以垂直板面方向即z方向为主，因此提取5#、6#、7#传感器z方向的响应进行比较（为便于比较，设定相同的横轴和纵轴范围），如图3所示。

图3 结构板上传感器z向的加速度时域响应Fig. 3 Time-domain acceleration response in z direction on the structural plate

5#、6#、7#传感器的时域振动响应峰值分别为0.100 g、0.720 g、0.049 g，这说明越靠近支架边缘，振动响应越大，而越靠近隔板或承力筒则响应越小。因此要使电子设备避开飞轮引发的振动干扰，应将其尽量远离支架并靠近隔板或承力筒进行布置。

对采集到的各测点不同转速下的时域数据进行频谱分析，部分结果见表1。

表1 不同转速下传感器响应幅值Table 1 Sensor response amplitude at different speeds

如表1显示：如果将工作转速从5 400 r/min下调到4 200 r/min，则无论是支架上的还是结构板垂直方向上的振动响应均可下降到原来的10%以下。

根据无阻尼单自由度结构振动理论，可估算降速之后振动响应幅值与降速之前的比值为(5 6702-5 4002)÷(5 6702-4 2002)=20.6%。如果与共振状态相比，则下降更为明显。因此，采取降低飞轮转速的措施来减小扰动是有效可行的。

3.2 增加刚性过渡板条件下的飞轮测试结果

测试前，在服务舱Ⅲ象限基准A飞轮的安装板上增加一层2 mm厚的钢板作为结构加强措施；试验时加装了侧板。加速度测试传感器布置如图4所示。其中，1#、2#、3#传感器布置在支架上，4#在轮缘上，5#、6#、7#分布在支撑板上，其中6#靠近支架边缘，5#和7#靠近中心承力筒。

图4 服务舱第III象限基准A飞轮的测点布置Fig. 4 Measurement point layout of flywheel A on the left lower quadrant of the service module

分别进行两种工况试验：

1）飞轮从3 000 r/min加速到6 000 r/min，1#传感器时域响应未见明显振动峰值（见图5(a)）；

2）飞轮从5 500 r/min加速到7 000 r/min，可以看到强烈的振动峰值（见图5(b)）。

为便于比较，图5中两个时域响应图的纵轴坐标范围相同。

图5 1#传感器x、y、z方向加速度时域响应Fig. 5 Acceleration responses in x, y, z directions for sensor 1#

时域响应显示的 1#测点（支架上飞轮转轴附近）x、y、z方向的振动幅值约为1.3 g、3.6 g、0.27 g。对第二次试验结果做FFT平均谱（见图6），得到振动峰值处的频率为 109.5 Hz，其对应转速为6 570 r/min。这说明通过增加结构刚度，可明显提高共振频率。

图6 转速5 500～7 000 r/min时1#传感器x、y、z方向的FFT平均谱Fig. 6 FFT spectrum in x, y, z directions at 5 500～7 000 r/min for sensor 1#

在不加装侧板的情况下，无钢板和有钢板加强措施的共振频率分别为 66.41 Hz、75.50 Hz（如图 7），与加装侧板后试验验证的有钢板加强措施所产生的移频效果是一致的。但这两个频率明显小于109.5 Hz的共振频率，究其原因是未加装侧板刚度偏弱所致。

图7 两种条件下x、y、z三方向响应历程的FFTFig. 7 FFT of response history in x, y, z directions under two conditions

通过实测转速下的时间历程谱分析可见，飞轮上测点响应与转速有很强相关性，因此考虑降低飞轮转速，以减小振动响应量级并改变共振频率。表2列出了不同转速下加速度响应幅值。

表2 不同转速下传感器响应幅值Table 2 Sensor response amplitude at different speeds

如果转速从5 400 r/min下降到4 200 r/min，对于扰动较为强烈的支架以及结构板上紧靠支架边缘的测点（如6#），其响应衰减为原来的20%左右。根据振动理论估算为(6 5702-5 4002)÷ (6 5702-4 2002)=54.9%，即使是结构板上离支架较远的测点（如5#、7#），响应也减小为原来的40%～50%。因此，采取降低飞轮转速的措施来减小扰动是有效可行的。

比较表1和表2发现：采用钢板加强措施之后，降速达到的减振效果不如未加强的。究其原因应该是钢板加强后提高了共振频率，5 400 r/min和4 200 r/min两个转速均远离了共振频率。

4 减振方案验证试验

经过以上试验得知飞轮扰动的形式和量级，也基本确定了引发结构共振的频率。基于相关测量数据和试验验证工作，对飞轮进行了减振设计：其中一个方案是加装吸振器，另一个方案是加装摩擦阻尼支架。然后对二者分别进行试验，以验证它们的减振效果。采取减振设计的飞轮仅针对服务舱第III象限基准A飞轮，其转速范围取3 000～6 000 r/min。

4.1 局部采取钢板加固但无减振设计的飞轮的验证试验

针对基准 A飞轮进行了钢板加固，开展了验证试验以测试默认状态以及钢板加固后的振动响应。提取了垂直于加固钢板方向（z向）4个通道（3-1通道位于轮缘上，3-2通道位于支架转轴附近，3-3、3-4通道位于加固钢板上）的峰值保持平均谱，如图8所示。

图8 基准A飞轮钢板加强前、后各通道Z向响应比较Fig. 8 Comparison of z-direction responses of flywheel A with and without the steel plate

在不加装侧板的情况下，钢板加固后使得结构共振频率从66.41 Hz上升到75.50 Hz，提升百分比为13.7%。3-1通道（轮缘上）的共振频率变化不大，其幅值较小；其他3个通道的振动幅值下降较为明显，从约1.0 g衰减到了0.1 g。

飞轮在轨实际工作转速约为5 400 r/min，相当于工作频率为90 Hz，与最初无刚性过渡板的共振频率94.5 Hz相当接近。在加装侧板条件下，使用了钢板加固后，基准A飞轮共振频率为109.5 Hz，比加固前提升了15.8%，有效避开了在轨工作频率（90 Hz），响应则明显下降。

根据单自由度结构振动理论估算，加固前、后的响应幅值之比为（109.52-902）÷（94.52-902）=4.69，也就是说，结构加固后使响应降低78.7%。如果进一步降低飞轮转速，则响应降低的效果还将进一步提高。

当然，结构加固除了降低振动响应之外，还可以提高结构的可靠性，而减振措施就不具备这个作用。

4.2 采取吸振器设计的飞轮的验证试验

增加了吸振器的飞轮装置以及传感器测点布置如图9所示。

图9 增加了吸振器的飞轮装置及传感器布置Fig. 9 Flywheel with additional vibration absorber and the layout of its sensors

根据振动理论，吸振器安装在飞轮支架上，可视为两个振子串联的结构：一个振子为吸振器，另一个为支架。其耦合频率有两个：一个大于两个振子固有频率的较大者，另一个小于两个振子固有频率的较小者。吸振器的设计频率约为 80 Hz。吸振器的减振目的是将耦合频率的较大者右移到飞轮转速范围之外，这虽然会产生较小的共振频率，但其扰动力量级较小。

吸振器的减振效果究竟如何，需要重点关注并评估支架本身以及结构板上靠近支架边缘的位置等部位的响应。为此，吸振器采用了单自由度可调设计：

1）小质量块可在后支杆上移动以调节频率（移动范围为0～40 mm），并可锁定位置固定频率；

2）对完全相同的 4根后支杆，表面分别敷设1 mm和4 mm厚的丁基橡胶阻尼层，另取1根未敷阻尼层的后支杆以对比研究阻尼层的减振效果。

分别取无阻尼和两种厚度阻尼层的后支杆，以及调节小质量块处在最近端和最远端位置，合计有6个状态进行试验，然后将这些试验结果与不安装任何减振装置的原始状态作对比。

小质量块处在后支杆最近端，阻尼层取 4 mm状态下的1#传感器时域响应与FFT平均谱如图10所示。安装吸振器之后，结构的共振频率发生了漂移，变为77.8 Hz。

图10 安装吸振器之后1#传感器x、y、z方向的响应Fig. 10 Response of sensor 1# in x, y, z directions with the vibration absorber

表3给出了各个测点响应的FFT平均谱与实时谱分析结果。考虑到垂直方向振动给层板结构带来的隐患较大，所以重点确定了1#传感器z向（记为1#-z）的共振频率以及该频率对应的响应幅值，另外还列出了支架上2#传感器的响应幅值。

表3 不同工况下峰值频率及响应幅值Table 3 Frequency and amplitude of the response under different conditions

表3显示：

1）吸振器减振性能对阻尼选择、质量块位置等设计参数具有很强的敏感性，但未发现减振效果有严格单调的变化趋势。如要获得最好减振效果，则需要通过数学仿真计算以寻求最优的参数并反复试验验证。考虑到实际卫星结构可能因环境或者老化而发生改变，吸振器原有的理论最优设计未必可以保证在卫星工作寿命期内始终获得最好效果。因此，吸振器的敏感性也成为阻碍其应用的一个缺陷。

2）采用阻尼材料后响应幅值均较工况②有所下降，因此阻尼层对吸振器是必要的。虽然工况①效果是所有工况中最好的，但鉴于无阻尼状态下吸振器响应过大可能导致疲劳寿命缩短的问题，故不宜采用。

3）对比工况③和④，以及工况⑤和⑥，可以看出小质量块在后支杆上的移动对频率影响并没有收到明显的效果。

为进一步显示吸振器的效果，图 11给出了 4个通道 1#-z、2#-x、2#-y、2#-z分别在工况⑥（加吸振器）、工况⑦（无吸振器）下的线性平均谱。

图11 各通道在安装吸振器前、后频谱比较Fig. 11 Spectrum of each channel with and without the vibration absorber

图11显示，吸振器的确使得在结构响应曲线的共振峰附近出现了凹峰——这证实了其吸振效应的存在。同时也可以看到，紧邻共振峰两侧，安装吸振器之后的响应比原始状态下的响应有所上升，而距离共振频率较远的地方基本上无改善效果，这与振动理论对吸振器的评价是一致的[5]。

4.3 增加摩擦阻尼支杆的飞轮验证试验

增加了摩擦阻尼支杆的飞轮装置以及传感器测点（3个）如图12所示。根据现场实测以及理论推算都可断定垂直隔板方向的响应较另两个方向为大，因此隔板的响应水平评价以 3#传感器 x方向为准。

图12 安装了摩擦阻尼支杆的飞轮装置及传感器布置Fig. 12 Flywheel with friction damping strut and the layout of its sensors

试验中连续 3次增加可调节摩擦螺钉的预紧力，支架受到阻尼支杆的摩擦力依次递增，3种情况分别记为工况一、工况二和工况三。为便于对比，最后撤除所有减振装置（即恢复原始状态），进行了相同的测量，典型频谱如图13所示。图中红色曲线为1#-z的频谱，绿色为2#-x的，蓝色为2#-y的，黑色为2#-z的。不同工况下的响应数据见表4。

图13 安装摩擦阻尼支杆前、后频谱比对Fig. 13 Spectrum before and after the installation of friction damping strut

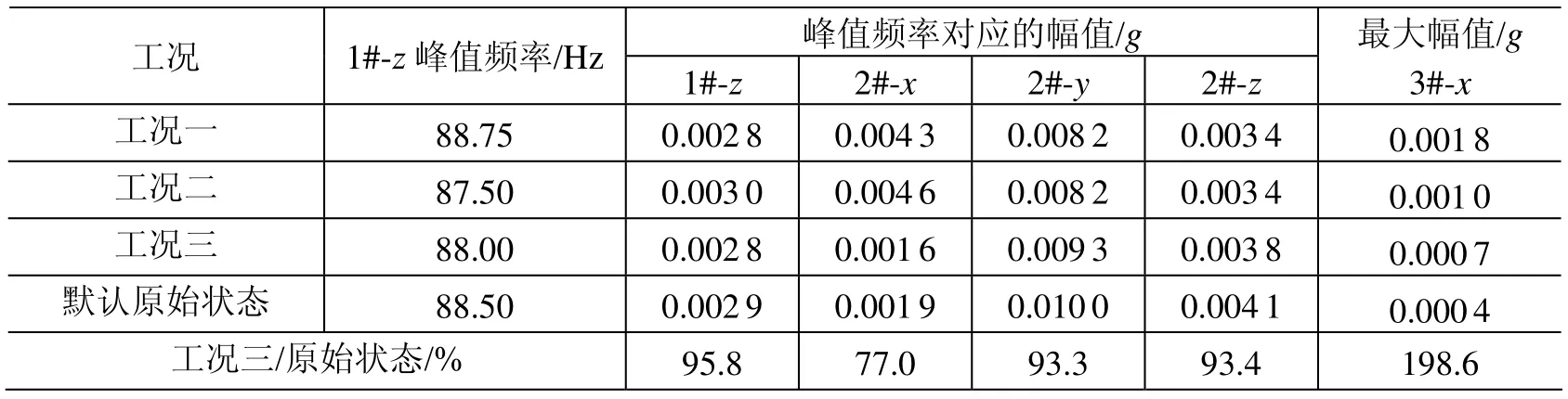
表4 不同工况下峰值频率及响应幅值（线性平均）Table 4 Peak frequency and amplitude of the response under different conditions (linear average)

表4显示，采用摩擦阻尼支杆对层板垂直方向的刚度影响较小，所以1#-z峰值频率几乎无变化。总体上看来，增大预紧力以提高摩擦阻尼对响应的改善程度有限，而且与原始状态相比可能会增大隔板上的响应。工况三与原始状态的 2#-z响应频率对比曲线如图14所示。

图14 工况三与原始状态的2#-z响应频率曲线对比Fig. 14 Response comparison of 2#-z between the working condition III and the original state

由图14可见，在60～100 Hz内，摩擦阻尼支杆对于峰值频率附近的响应有一定改善，其他区域效果不明显。

5 结论

1）结构板加强是飞轮减振行之有效而且具有较高可靠性的措施。

2）在设计条件允许的情况下，适当降低飞轮转速，即将工作转速从5 400 r/min降低到4 200 r/min可以显著地减小振动响应，使得不平衡所产生的激励力大幅下降，所激励的响应也会明显削弱。

3）吸振器减振性能对结构参数变化较为敏感。在阻尼较低的情况下，响应偏大，对其自身可靠性影响较大，目前不适于星上使用。

4）摩擦阻尼支杆的使用导致侧板响应增大且减振效果不明显，考虑其还具有摩擦运动生热以及产生多余物等缺陷，因此也不适于星上使用。

（References）

[1]孙贤军, 王树文, 张天序. 反作用轮扰动对三轴稳定地球同步卫星姿态影响分析[J]. 计算机与数字工程,2005, 33(12): 55-59 Sun Xianjun, Wang Shuwen, Zhang Tianxu. Effects of reaction-wheel induced disturbance on the attitude of three-axis-stabilized geostationary satellite[J]. Computer& Digital Engineering, 2005, 33(12): 55-59

[2]尹秋岩, 赵健康, 戴金海. 反作用飞轮内干扰抑制方法研究[J]. 电子与信息学报, 2007(6): 1521-1524 Yin Qiuyan, Zhao Jiankang, Dai Jinhai. A method of control inner disturb to the reaction wheel[J]. Journal of Electronics& Information Technology, 2007(6): 1521-1524

[3]王全武, 虎刚. 飞轮扰动原因与测量技术现状[J]. 空间科学学报, 2009, 29(1): 40-41 Wang Quanwu, Hu Gang. Analysis of flywheel disturbance and measuring technology[J]. Chinese Journal of Space Science, 2009, 29(1): 40-41

[4]章仁为. 卫星轨道姿态动力学与控制[M]. 北京航空航天大学出版社, 1998: 139-175

[5]屠善澄. 卫星姿态动力学与控制[M]. 4版. 北京: 中国宇航出版社, 2006