基于超声波电机的三维微动平台的设计*

王 帅，苏 刚

(1.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016;2.中国科学院研究生院，北京 100049）

0 引言

精密运动平台是指行程小、分辨率和精度高的运动平台，是精密机构与精密仪器的组成部分之一［1］。它既是重要的进给元件，也是对工艺系统误差进行动态、静态补偿的关键元件，直接影响精密、超精密切削加工水平、精密测量水平及超大规模集成电路生产水平的关键环节。因此，精密运动平台成为国内外研究热点。

目前，大多利用压电陶瓷作为驱动装置对平面工作台进行精细的位姿调整，但是其系统需要电压高，驱动电路较为复杂［2］，不适用航空和宇航领域所要求的低电压、轻量化等适合太空环境的特点。而超声波电动机具有驱动电压低、小型轻量、响应速度快、能获得低速大转矩和可用于直接驱动、断电时具有高自锁力矩，不受电磁场干扰等优点［3］。因此，面向空间生物医学用三维微动平台采用超声波电机进行驱动。但是，采用超声波电机驱动方式的微动平台驱动力小、行程大，因此采用缩小机构将执行器的位移缩小再传递给输出端以提高运动精度。而且由于柔性铰链具有体积小、无间隙、无机械摩擦、运动灵敏度和分辨率高等优点，柔顺机构依赖于柔性构件的变形，其能量便以应变能的形式储存在柔性构件中，利用储存在柔性构件中的应变能可实现微动平台的微位移［4］。因此，研究基于柔性铰链微位移缩小机构对面向空间生物医学用三维微动平台的研制具有重要意义。

1 微动平台的设计与制作

面向生物医学实验用空间手套箱开发的超声波电机驱动的微动平台，根据操作对象的几何尺寸、微尺度下的受力特点，拟定微动平台的设计指标为:工作空间为90μm×150μm×150μm，精度为亚微米级。本微动平台主要用于对末端探针进行微位姿调整，从而实现对细胞的微操作。图1为微动平台柔性铰链模型图。根据伪刚体模型法［5］，圆弧型柔性铰链处看作是含扭转弹簧的活动铰链，其他杆件为刚性杆。其中孔k1、k2、k3、k4通过螺钉与基座固连作为支点。根据杠杠原理，当下部的杆L1受到向内的推力时，上部的杆L2向上运动，反之，当下部的杆L1受到向外的推力时，上部的杆L2向下运动。当相对的两个杆L1、L3向同方向运动时，微动平台可以实现一个方向的自由度，即向X或Y方向运动;当四个杆同时向内或向外推时，微动平台可以实现Z方向的运动，这样即可实现三个自由度的运动。

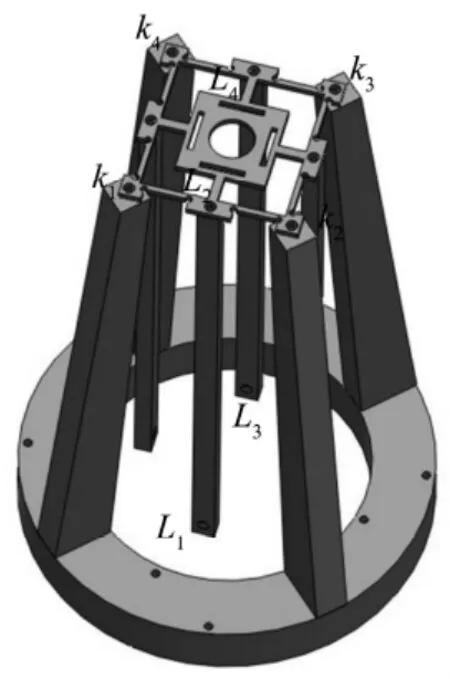
图1 柔性铰链模型

取微动平台的1/4进行分析，机构的受力分析如图2所示。根据单轴柔性铰链的设计计算公式［6］和杠杆定理可得:

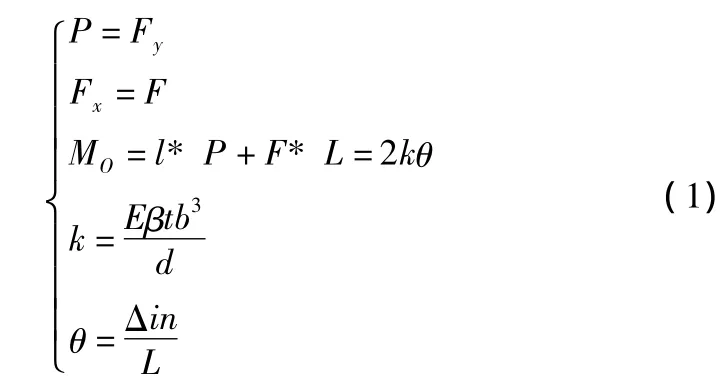
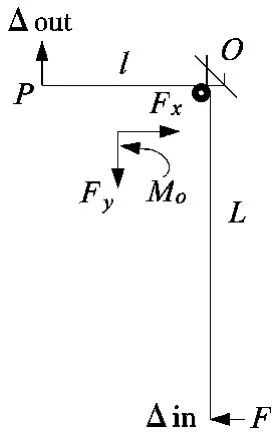
图2 机构的受力分析

整理得:

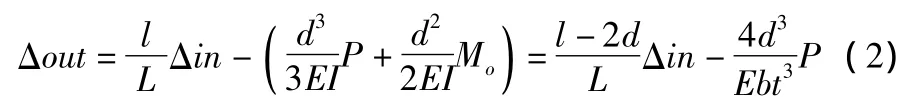
负载忽略不计，带入数值，缩小倍数为0.025。

2 微位移缩小机构运动学分析

由于微动机器人的运动范围小，与传统的机器人比，在运动学等方面有其自身的特殊性［7］。因此，采用微分法，对三自由度并联微动平台进行运动学分析。上平台有3个自由度，其运动是有4个超声波电机驱动底部杠杆并通过缩小机构来实现的。4个连杆分别用A-a、B-b、C-c和D-d表示，其中A、B、C、D 为支柱与基座的连接点，a、b、c、d 为支柱与上平台的连接点。建立固定坐标系OXYZ和动坐标系oxyz。取A、B、C、D构成的正方形的中心O为固定坐标系OXYZ的原点，X轴通过AB和CD的中点，Y轴通过AD和BC中点，指向如图3所示。动坐标系oxyz的原点取为运动平台上 a、b、c、d构成的正方形的中心，x轴通过ab和cd的中点，y轴通过ad和bc的中点。

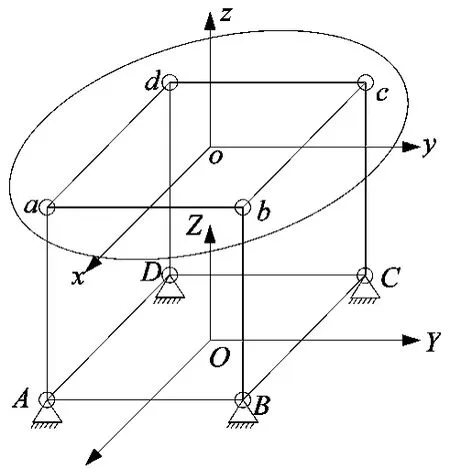
图3 坐标系设定

当超声波电机驱动下端连杆运动时，引起动平台沿X、Y、Z轴的平动可用以下公式描述:

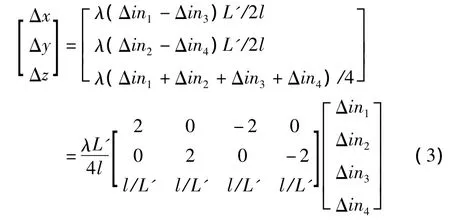
式中:λ为微位移缩小机构的位移缩小倍数;Δini(i=1，2，3，4）为超声波电机输入位移量，L'为微动平台上端物体的长度。带入数值，Δx、Δy、Δz分别为167.5μm、167.5μm 、90.3μm。

3 ANSYS的有限元分析验证

采用解析法对柔性铰链进行计算时，假设除了柔性铰链外微位移机构其余部分均为刚体［8］，而在实际应用中，整个柔性铰链机构是一个弹性体，因此实际应用与理论计算之间会存在一定误差。利用有限元分析软件对微位移机构在极限工作状态下进行结构静力分析，主要考虑微位移机构在载荷作用下的形变量大小及工作部分的位移是否满足设计要求［9］。

首先，利用Solidworks软件建立微位移机构三维模型，然后根据有限元分析的需要用其自带软件Solidworks Simulation合理地划分网格，设置材料为铝合金7075(密度为2.85g/m3，弹性模量72Gpa，泊松比为0.33，屈服强度570Mpa），对其四个分支分别施加向内0.5N的作用力后，柔性机构的极限位移如图4a所示。从图中可以看出柔性机构实现了Z向的移动90.8μm。其应力云图如图4b所示，最大应力341.4Mpa，小于许用应力，符合设计要求。对其相对的两个分支分别施加向内0.5N的作用力后，柔性机构的极限位移如图4c所示。从图中可以看出柔性机构实现了X、Y向的移动166.4μm，其应力云图如图4d所示，最大应力479.2Mpa，小于许用应力，符合设计要求。

图4 仿真结果

4 实验验证

为了精确测出三个自由度的运动距离，搭建了微位移工作台试验系统。该系统由控制计算机、微位移工作台、探针、摄像头装置等组成。微位移工作台实验系统中最重要的部分是微位移工作台，它是整个实验系统的核心，如图5所示。

图5 微动平台实物图

面向生物医学实验用超声波电机驱动微动平台，采用超声波电机(SQL-RV-1.8(2.8×2.8×6mm），最大位移6mm，最大力 0.5N，精度0.5μm）进行驱动。对比匹配点的初始位置和运动后位置(如图6所示），可以得到X、Y向位移为168.1μm，Z向位移为89.8μm。经过验算，与理论计算差异小于5%，从而验证了理论的正确性。

图6 微动平台实验图像

5 结束语

本文设计了一种采用超声波电机驱动的微动平台的模型，该微动平台采用柔性位移缩小机构提高运动精度，实验证明该微动平台工作空间为90μm×168μm×168μm，具有亚微米级运动精度。

对比有限元仿真和理论分析发现:由于理论分析假设系统除了柔性铰链部分外其他部分是刚性，系统其他部分的变形影响了系统的运动缩小倍数和应力分布。但两者结果相差不大，实际设计中可以先用理论模型进行设计，再用有限元模型校验。在柔性铰链微动平台设计中，加强机构中柔性铰链固定端和杠杆臂的刚度可以使理论结果和有限元分析结果更接近。

［1］谢卫东.精密微位移工作台系统综述［J］.自动化与仪器仪表，1991(1）:8-9.

［2］丁晓辉，董再励，刘柱，等.纳米级微动平台的结构力学特性及实验研究［J］. 机器人，2010，32(3）:321-325.

［3］贠远，徐青松，李杨民.并联微操作机器人技术及应用进展［J］. 机械工程学报，2008，44(12）:12-23.

［4］李庆祥，王东生，李玉和.现代精密仪器设计［M］.北京:清华大学出版社，2004.

［5］Howell L L.Compliant Mechanisms［M］.New York:John Wiley and Sons Inc，2001.

［6］鹰飞，周兆英.柔性铰链的计算和分析［J］.机械设计与研究，2002，6(3）:29-30.

［7］立宁，安辉，张涛，等.微动运动学分析的基础研究［J］.仪器仪表学报，1998，19(5）:464-470.

［8］立峰，李蓓智，杨建国，等.压电驱动微进给工作台设计与性能研究［J］. 压电与声光，2007，29(2）:240-242.

［9］张磊，刘莹.基于柔性铰链的微位移机构设计［J］.机床与液压，2010，38(5）:87-89.