卧式加工中心误差建模与补偿技术的研究*

范晋伟，雒 驼，李 云，蒙顺政，李 伟，罗建平

(北京工业大学机电学院，北京 100124）

0 引言

四轴卧式加工中心由于可进行多面加工，其刚度和稳定性又优于普通的五轴机床，在加工精度与加工效率的平衡上，卧式精密加工中心具备三轴与五轴机床都不具备的优势。但是在零件的实际加工过程中，由于机床各环节都不可避免的存在误差，通过运动链最终都会影响机床的加工精度，直接影响汽车、微电子、航空航天、武器制造等工业领域中最终产品的质量，影响着行业的整体发展。所以在保证加工效率的基础上如何有效的提高加工精度是当前亟待解决的问题。

提高机床的精度有两种方法，误差防止法和误差补偿法。其中误差补偿法通过误差补偿软件预先修正机床加工指令，进行误差补偿，使刀具轨迹满足精度要求。为机床建立合适的误差模型，是误差补偿法的关键步骤之一。

机床误差中，几何误差、热变形误差、载荷误差和刀具误差占总误差的70% ～90%［1］。其中几何误差及在稳定工作状态下的热变形误差都属于稳定的系统误差，最高可占总误差的65%［1］，几何误差模型就是将这部分误差产生的几何变形映射到几何误差上来分析。因此，几何误差建模实际上并不限于分析几何误差，是一种综合空间误差建模，具有误差补偿效果好，补偿效果稳定，不受误差形式局限的优点。本文误差建模的主要目标是以多体系统理论为基础，建立综合空间误差模型与刀具姿态误差模型，为误差补偿打下理论基础。

在建立综合空间误差模型的基础上，还要有合适的误差补偿方法才能对机床数控指令进行修正。本文分析了刀具轨迹与数控指令映射关系，选择采用迭代法添加判定条件的手段修正数控指令。

最后，本文针对四轴卧式加工中心的机床结构与误差形式，以多体系统理论为基础，为加工中心建立了综合空间误差模型以及刀具姿态误差模型，以误差模型和刀具轨迹与数控指令的映射为指导，编写了基于C++的刀具轨迹仿真软件。并对理想刀具轨迹、实际包含误差的刀具轨迹以及补偿后的实际刀具轨迹都进行了仿真，验证了误差建模环节的正确性以及误差补偿的有效性。

1 卧式加工中心的几何误差模型

1.1 基于多体系统理论的机床结构描述

四轴卧式加工中心是由床身、X轴导轨、Y轴导轨、主轴、刀具、Z轴导轨、工作台、工件所组成的多体系统。其结构简图如图1所示，图2为根据结构简图提炼出的拓扑结构。根据多体系统基本理论，以其特有的低序体阵列描述多体系统的拓扑结构，任意物体的较低序号的物体，用L(K）表示，L表示低序体算子，K表示物体的序号，它满足:

且补充定义L(K）=K，L(0）=0。则车铣中心的拓扑结构各体的各阶低序体序号，如表1所示。表2为其自由度，它表示机床各单元之间的约束情况，其中“0”表示不能自由运动，“1”表示能自由运动。

图1 四轴卧式加工中心的结构简图

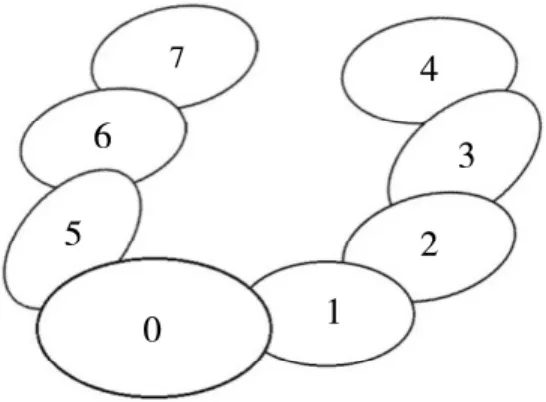
图2 四轴卧式加工中心的拓扑结构图

表1 四轴卧式加工中心的低序体阵列

表2 加工中心运动轴的自由度

1.2 四轴卧式加工中心的误差分析

四轴卧式加工中心共有47项几何误差，首先X、Y、Z三个平动轴各有6个，共计18项误差项，以X轴为例，有定位误差、Y方向直线度误差、Z方向直线度误差、滚摆误差、颠摆误差、偏摆误差:Δxx、Δyx、Δzx、Δαx、Δβx、Δγx;其次转动轴 B 有 6 项误差，X 方向跳动误差、Y方向跳动误差、轴向窜动误差、绕X轴转角误差、绕Y轴转角误差、绕Z轴转角误差:ΔxB、ΔyB、ΔzB、ΔαB、ΔβB、ΔγB;主轴有 6 项误差，X 方向跳动误差、Y方向跳动误差、轴向窜动误差、绕X轴转角误差、绕 Y 轴转角误差、绕 Z 轴转角误差:Δxφ、Δyφ、Δzφ、Δαφ、Δβφ、Δγφ;工件及刀具装夹各有 6 个总共12项误差，以工件为例:X方向直线度误差、Y方向直线度误差、Z方向直线度误差、绕X轴转角误差、绕Y轴转角误差、绕 Z 轴转角误差:Δxwd、Δywd、Δzwd、Δαwd、Δβwd、Δγwd;另有5 项单元间姿态误差:X、Y 轴垂直度误差、X、Z轴垂直度误差、Y、Z轴垂直度误差、B 轴与 X、Z 轴间的垂直度误差 2 项:Δγxy、Δβxz、Δαyz、ΔγxB与 ΔαzB。需要注意的是，由于研究初衷是为了补偿机床在测量后一段有效时间内的稳定误差，我们忽略了与装夹及更换刀具有关的易变误差、可以随时测量调整的B轴与X、Z轴肩的垂直度误差，以及与刀具具体形态有关的主轴误差，只留下机床中不轻易改变的27项固有几何误差进行建模。

1.3 基于多体系统理论的四轴卧式加工中心误差建模

空间综合误差及姿态误差推导所使用的四轴卧式加工中心的体间理想静止(运动）特征矩阵Tijp(a）、体间静止(运动）角误差矩阵Tijp(a）(R）及体间静止(运动）误差特征矩阵ΔTijp(a），均可由多体系统特征矩阵表［3］推出。

设刀具成形点在共建坐标系内的坐标是:

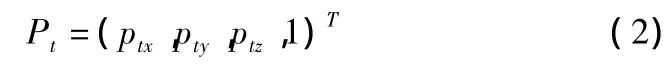
那么刀具成形点在工件坐标系内的理想成形函数为:

在四轴卧式加工中心上，由于进给系统中有一个回转运动，为成形过程中调整刀具与工件间的相对姿态提供了一定条件，在加工工件的复杂曲面时能在一定程度上提高精度，为此也需要控制成形过程中的刀具姿态。为了描述刀具的位姿变化，我们在刀具上固定一矢量，使其随刀具一起运动，然后考察该矢量的转动情况。设刀具上刀柄至刀尖两点之间的矢量V在刀具坐标系中的表达式为:

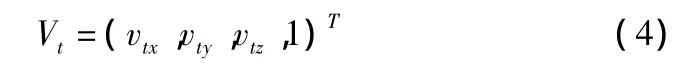
那么理想运动条件下，矢量V在工件坐标系中的表达式为:

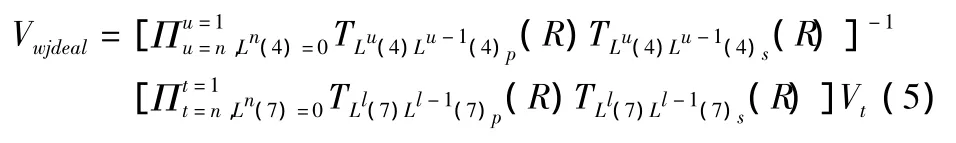
在机床的实际加工过程中，由于存在各种误差，所以刀具成形点在工件坐标系内的实际成形函数和无误差的理想加工过程不同，其实际成形函数为:

同理，在实际加工过程中刀具的姿态与理想加工过程中刀具的姿态也不相同，实际加工运动矢量V在工件坐标系中的表达式为:

在实际加工过程中，刀具成形点的实际位置由于各误差项的影响会偏离理想位置，产生综合空间位置误差。根据上文所述的坐标系间变换矩阵，即式(2）、(3）、(6）可对理想的成形空间点和实际刀具成形空间点进行坐标变换，以求解出刀具成形点的综合空间误差，其为:

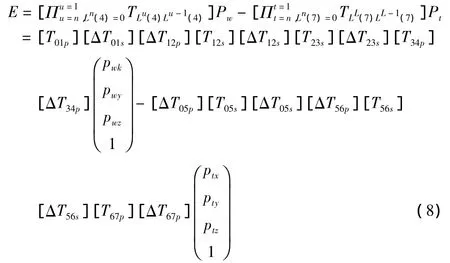
加工过程中，刀具相对于工件的实际姿态与理论姿态间，由于受到旋转轴及平动轴误差的叠加影响，也会存在偏差，这里用E表示，根据式(4）、(5）、(7），可得刀具的空间姿态误差为:

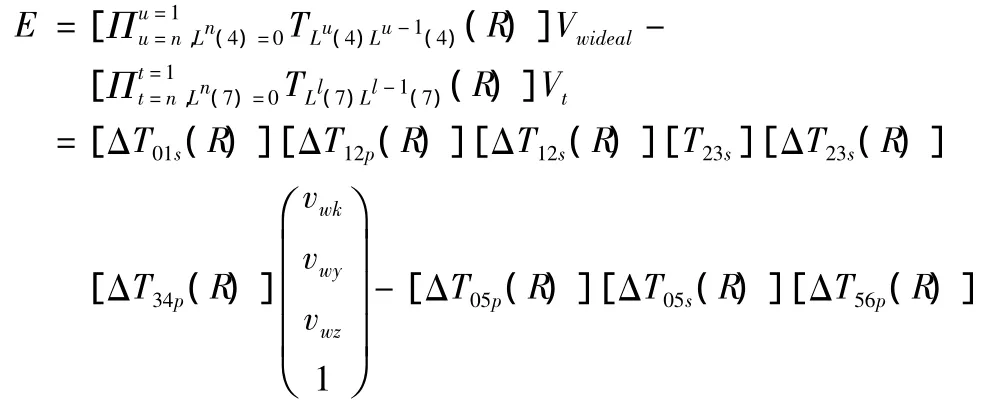
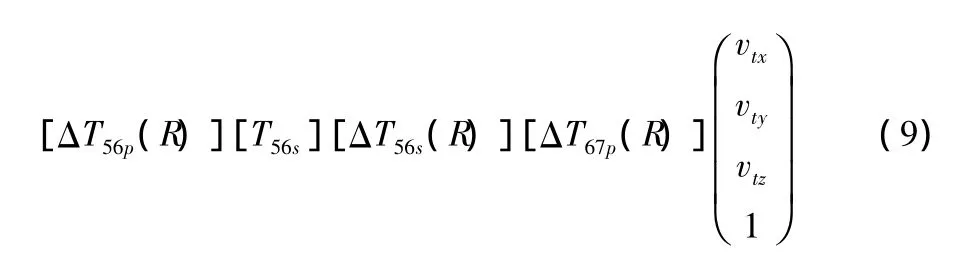
根据多体系统理论，经过运动误差分析，式(8）、(9）就是四轴卧式加工中心刀具成型点的综合空间运动误差模型及刀具空间姿态模型。该模型为进行误差补偿和编写误差补偿仿真软件提供了理论基础。

2 数控指令修正值求解

2.1 刀具轨迹的表达

刀具轨迹指的是机床刀具中心在工件坐标系内的运动轨迹，它有理想刀具轨迹和实际刀具轨迹之分，理想刀具轨迹指的是根据理想的机床运动模型，经理论计算而得的刀具轨迹;实际刀具轨迹指的则是机床刀具在相对于工件坐标系运动过程中实际产生的轨迹。

在理想条件下以及实际条件下，建立起数控指令及刀具轨迹二者间的相互映射关系，是软件误差补偿的关键环节之一。通过这些映射关系，不仅可以获得修正后的数控指令，而且还可以进行仿真和分析。

由于一条刀具轨迹上有无限个点，再考虑到数控指令的长度要求等问题，不可能去逐点控制刀具轨迹，只能通过修正映射关系的方法来控制刀具轨迹。

在理想条件下，不存在加工误差。数控指令到刀具轨迹的映射关系不受误差影响。而在实际条件下，映射关系则由误差参数确定。

2.2 采用迭代法修正数控指令

为求得修正后的数控指令，误差补偿软件采用迭代计算法直接修正数控指令。其计算步骤是:首先根据刀具轨迹与数控指令的关系求出迭代初值(x0，y0，z0）;其次将初值代入刀具轨迹与数控指令实际的映射关系，得到一次迭代后修正的数控指令值(x1，y1，z1）;然后判断所得的修正数控指令所驱动的实际刀具轨迹与理想刀具轨迹上相应点的位置偏差是否小于给定值，如果满足判别条件则迭代完毕;如果不满足判别条件，则以(x1，y1，z1）为初始值继续迭代，直到满足条件位置。设第i次迭代终止，则得到满足条件的修正后数控指令值为(xj，yj，zj），迭代的终止条件为:

式中 Δx、Δy、Δz分别为机床 X、Y、Z 轴的平移分辨率;Δα、Δβ、Δγ分别为机床绕 X、Y、Z 轴转动的分辨率。

3 仿真结果

依据四轴卧式加工中心的综合空间误差模型、刀具姿态误差模型与迭代法修正数控指令的方法，我们开发了基于C++的误差补偿仿真软件。该软件可以以综合空间误差模型为基础，生成加工中心的运动误差模型。该仿真软件的输入包括选取四轴卧式加工中心的结构参数、人工设定或导入误差参数、导入理想数控指令G代码文件;输出则包括生成理想刀具轨迹、生成实际刀具轨迹以及生成补偿后的实际刀具轨迹，同时也可以导出修正后的数控指令G代码(图3）。

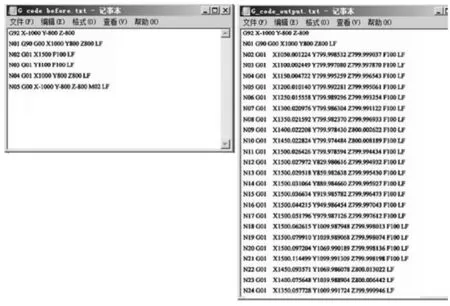
图3 数控指令修正前后的G代码对比

通过导入项目组实验测定的机床误差数据文件，依据给定的理想数控指令，仿真软件即可显示理想刀具轨迹与实际刀具轨迹在补偿前后的图形对比(图4）。

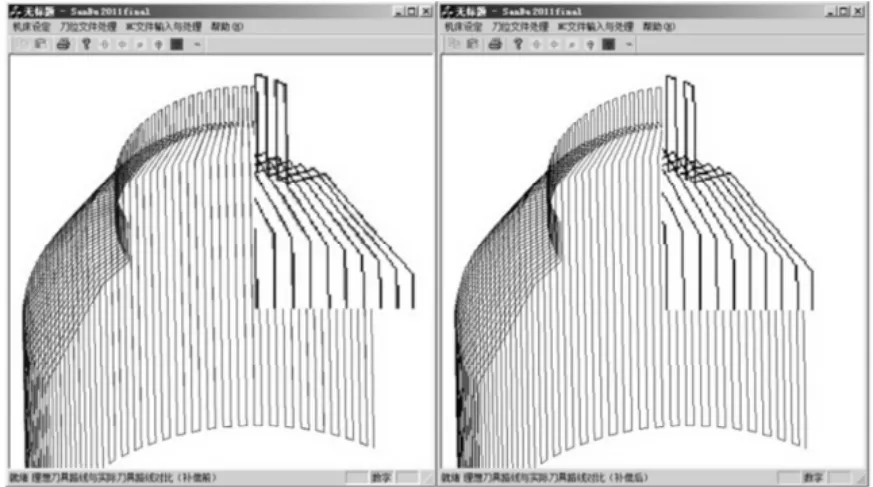
图4 理想刀具路线与实际刀具路线在补偿前后的对比

图中，蓝色线条表示的是理想刀具轨迹，绿色线条表示实际刀具轨迹，可以观察到补偿前图形中两轨迹不重合，而经过误差补偿后，实际刀具轨迹与理想刀具轨迹是重合的。这首先说明，在本次误差建模基础上编写的误差补偿软件确实生成了可行的刀具轨迹;其次说明引入的误差确实起到了改变实际刀具轨迹的作用;最后也证明了补偿算法确实对实际刀具轨迹进行了补偿。

4 结束语

(1）基于多体系统理论，以考虑位置误差与姿态误差的约束条件方程为前提，建立的四轴卧式加工中心的综合空间几何误差模型及综合空间姿态误差模型是正确的。且建模过程具有程式化，模块化，易于快速建模的特点。

(2）在数控指令和刀具轨迹的相互映射关系的基础上进行修正数控指令求解的补偿算法是可行的。补偿前后的刀具轨迹对比图表明，以此算法为基础的仿真补偿软件确实对实际刀具轨迹进行了有效的补偿。且具有低成本、效果好，准确快捷的优势。

［1］盛伯浩.数控机床误差的综合动态补偿技术［J］.制造技术与机床，1997(6）:19-21.

［2］范晋伟.基于多体系统运动学的数控机床运动建模及软件误差补偿技术的研究［D］.天津:天津大学，1996.

［3］李圣怡，戴一凡.精密和超精密机床精度建模技术［M］.北京:国防科技大学出版社，2007.

［4］粟时平.多轴数控机床精度建模与误差补偿方法研究［D］.长沙:国防科学技术大学，2002.

［5］刘又午，刘丽冰，赵小松，等.数控机床误差偿技术研究［J］. 中国机械工程，1998，9(12）:48-52.

［6］李小彭，刘春时，马晓波，等.数控机床加工精度提高技术的进展及其存在的问题［J］.组合机床与自动化加工技术，2010(11）:1-4.

［7］范晋伟.运用多体系统运动学理论建立数控机床空间误差模型［J］.北京工业大学学报，1999(2）:38-44.

［8］粟时平，李圣怡.多体系统理论在数控加工精度软件预测中的应用［J］.组合机床与自动化加工技术，2004(3）:26-30.

［9］任永强，杨建国，基里维斯，等.四轴数控机床误差综合建模原理及分析［J］.机械工程师，2003(8）:18-22.

［10］刘新宇.五轴数控机床回转工作台的设计［J］.组合机床与自动化加工技术，2009(6）:100-101.