某型通用机枪隔弹齿参数优化研究
张本军,王瑞林,李永建,和丽磊
(1.军械工程学院,河北 石家庄 050003;2.75130部队,广西 贵港 537103)
某型通用机枪存在首发装填困难的问题,其主要原因是装填过程中受弹机存在较大的阻力。受弹机在运动过程中,主要受到弹带运动阻力及脱弹过程中作用在拨弹板上的力。在手动装填过程中,弹带运动阻力相对较小,因此,减少拨弹板受力是解决首发装填困难的一个途径。
弹链对自动机产生的影响主要集中在弹链运动阻力上[1-4],针对脱弹过程对拨弹板作用力的研究相对较少,因此,要解决首发装填困难的问题,需要精确的研究受弹机运动过程中的阻力。
本文利用有限元接触理论,求解某型通用机枪的横向脱弹过程,进而给出一种求解脱弹过程对拨弹板作用力的方法。最后,对机枪隔弹齿的隔弹曲线进行优化设计,以期减小脱弹过程中拨弹板的受力。
1 脱弹过程求解
针对横向脱弹过程的分析,通常所使用的方法为阶梯形圆弧薄曲杆的方法[5]。该方法假设脱弹过程中链节的变形是对称的,这样将半个链节简化为一端固定,另一端支撑在刚性圆柱上的阶梯形圆弧薄曲杆。曲杆的横截面为矩形,其高等于链节厚度,宽度沿曲杆长度方向作阶梯形变化。该方法计算简单明了,应用比较广泛[6-7],特别武器的设计说明书中,应用的基本上都是这种方法。然而,该方法简化的过多,其计算结果可作为弹链初步设计时的参考,而想要得到更精确的计算结果,就需要一种更精确的方法。
1.1 基本假设
弹链的脱弹过程是相当复杂的,受供弹阻力、拨弹齿的压力、隔弹齿通过弹体传递的压力等作用。因此,需要作如下假设:
1) 弹链的变形在弹性范围内,不考虑弹链材料的非线性项。弹链在脱弹结束后,能够恢复到其初始状态,所以认为弹链的变形是在弹性范围内。
2) 求解过程中,弹体作为刚体进行处理。由于弹链开口的原因,使得弹体的刚度远远大于弹链的刚度,因此可将弹体作为刚体进行处理。
3) 认为弹链的变形完全是由弹链与弹体的过盈配合引起的,不考虑其它力引起的弹链变形。其它各种力综合引起的弹链的变形,相对于过盈配合引起的弹链变形是非常小的,可以忽略不计。
4) 认为脱弹过程中弹体的对称面与弹链的对称面始终重合,且不考虑惯性力的影响。
1.2 求解方法
横向脱弹过程从本质上讲是弹链与弹体弹性接触的过程,所以,可以利用有限元的接触理论对脱弹过程进行更精确的分析。本文从有限元接触理论的基本公式出发[8-9],推导了脱弹过程的计算公式。推导步骤及结果如下:
1) 利用枪弹参数,求得枪弹弹壳锥部外表面的函数以及各点法向量和切平面的表达式,建立局部坐标系。
2) 利用有限元接触理论中的不可穿透性和Coulomb摩擦模型给出弹链接触问题的定解条件和校核条件。
3) 分别用虚位移原理和引入罚函数的位能变分表示弹链的平衡条件,得到在局部坐标系下接触力与罚因子之间的关系。
4) 对弹链进行离散化处理,得到弹链各接触节点处的等效接触力与罚因子之间的关系式。
5) 将上一步得到的结果对所有接触的节点进行集成,可以得式(1)。
(1)

对于粘结接触状态:
(2)
对于滑动接触状态:
(3)
其中:g=[0,0,g3]T
式中:θ为局部坐标系与整体坐标系之间的转换矩阵,可以利用弹链节点的初始坐标与枪弹锥部点法线方程求得;g3为局部坐标系中初始法向穿透量;u1和u2分别是弹链节点在局部坐标系中两切向位移;uT为局部坐标系中切向位移向量;a1、a2和a3是罚因子;μ为摩擦因数。
所以弹链的有限元求解方程可以表示为:
(4)
式中:K为弹链在整体坐标系下的刚度矩阵;U为弹链各节点在整体坐标系下的位移向量。
利用Newmark算法求解式(4),得到弹链各节点的位移,进而求出等效节点力。这样,通过改变弹体的位置,就可以求得整个脱弹过程中弹链的受力情况。
与阶梯形圆弧薄曲杆方法相比,该方法考虑了弹链和弹体的锥度、应力沿弹链厚度方向的变化等,并且使模型可以更合理的添加边界条件,所以能够得到更精确的结果。
1.3 求解结果
利用所提出的方法对该枪的脱弹过程进行了求解,得到的结果如图1和图2所示。


图中正向压力代表的是弹链作用在枪弹上的垂直于脱弹方向的力。从图中可以看出,该枪在弹壳向弹链开口方向运动2.62 mm以后完成脱弹动作,即这时弹链的张开角达到180°;脱弹力在弹壳运动的初始阶段迅速增加到最大值154.6 N,之后开始减小,这是由接触面力与弹壳运动方向的夹角变化造成的;正向压力在初始阶段的减小是由于在初始阶段,接触面力增加速度远远小于脱弹力增加速度造成的。
2 拨弹板受力求解
在首发装填的过程中,枪弹在隔弹齿的作用下脱离弹链,其受力情况如图3所示。

图中F为拨弹板所受的力,N为隔弹齿隔弹曲线提供的支撑反力,P为脱弹力,Q=fN0为脱弹过程中正向压力提供的摩擦力,则可以得到:
F=tanα(fN0+P)
(5)
式中:f为摩擦系数;N0为正向压力。利用求得的脱弹力和正向压力以及隔弹齿曲线与枪弹接触点出的切线斜率,就可以求得F值。但是,这种方法对于隔弹齿曲线是直线的情况应用方便,但若隔弹齿曲线为一曲线,这种方法就不太适应,特别是在对曲线的参数优化上。基于此,本文提出了用ADAMS动力学模型进行等效的方法,如图4所示。

模型中将质量块进行限制,仅留方向x和y方向的平动自由度;将力fN0和P以样条曲线的方式添加到质量块的y方向;在质量块上创建一个Marker,让该点在隔弹齿曲线上运动;对质量块的方向添加一个位移驱动,这样就使得质量块质心的运动曲线与隔弹曲线保持一致。在计算过程中将质量块的质量设定为一个极小的数值,将驱动所带来的质量块的加速度也设定为极小的数值,这样模型的动力学求解过程就满足所提假设。又由于,在xy平面内曲线过一个定点的切线仅有一条,这样就保证了模型中曲线提供的支反力与图3所示支反力方向一致。因此,该等效方法是完全可信的。
3 优化计算
3.1 目标函数及优化参数的确定
为使加工方便以及不改变隔弹齿其他作用效果,本文将隔弹齿的隔弹曲线看做首末两端固定的圆弧线,而原始的直线可以看做半径无限大的圆弧。这样,待优化的参数为该圆弧的半径R。
隔弹齿对于首发装填困难影响最大的因素为拨弹板力的最大值,因此,本文的优化目标为拨弹板力的最大值最小。
拨弹板力的变化必然引起该枪在装填过程中的能量消耗,为不增加后坐过程中的能量消耗,应使优化后拨弹板力做功小于优化前做功;为保证枪弹在脱弹过程中一直向下运动,需要圆弧的弧度小于π/2。这样,隔弹齿的参数优化问题可以用数学模型表示为:
To findR
Minφ(R)=maxF
(6)
(7)
式中:W0为优化前F所做的功;R0为隔弹曲线弧度为π/2时的半径。
3.2 优化结果
应用区间消去法,利用ADAMS模型等效的方法对式(5)进行计算,得到在半径为R=45.5 mm时最优。与优化前进行比较,得到的结果分别为图5、图6和表1所示。
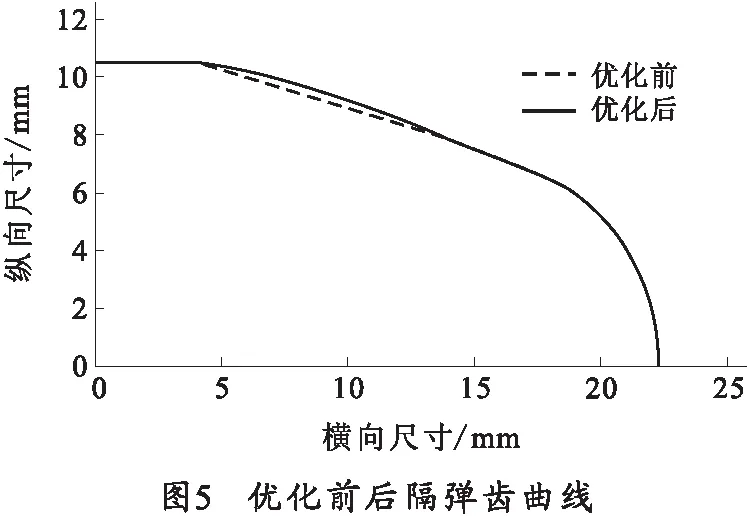


表1 优化前后最大力及做功的比较
从中可以看出,优化后,在做功减小的情况下拨弹板所受力的最大值减小了17.4%,且优化后拨弹板所受力变化较优化前平稳,这都有利于该枪的首发装填,从而达到了优化的目的。
4 结 论
本文利用有限元理论,求解了某型通用机枪枪弹的脱弹过程;利用ADAMS动力学模型等效的方式求解了脱弹过程中拨弹板所受的力;以拨弹板所受力的最大值最小为目标,以不增加拨弹板做功为约束条件,对隔弹曲线半径进行了优化研究。通过优化使拨弹板受力的最大值减小了17.4%,且优化后的受力变化较平稳,为解决该枪首发装填困难提供了一种有效的方法。
[1] 王光建,姜铁牛.弹链系统间隙铰多体动力学模型仿真与试验[J].机械工程学报,2008,44(5):238-241.
WANG Guang-jian, JIANG Tie-niu. Simulation and
experiment of multi-body system dynamic model with clearance joint for ammunition belt system[J].Chinese Journal of Mechanical Engineering,2008,44(5):238-241.(in Chinese)
[2] 杨军荣.弹链供弹阻力研究[J] .南京理工大学学报,1997,21(4):352-355.
YANG Jun-rong.Study of ammunition belt links feed resistance[J].Journal of Nanjing University of Science and Technology,1997,21(4):352-355.(in Chinese)
[3] 魏志芳,陈国光.根据供弹导引空间姿态计算自动机负载的方法研究[J].火炮发射与控制学报,2008(2):35-37.
WEI Zhi-fang,CHEN Guo-guang.Study on load calculation method of automatic mechanism according to feeding guide space and attitude[J].Journal of Gun Launch &Control,2008(2):35-37.(in Chinese)
[4] 韩魁英,王梦林,朱素君.火炮自动机设计[M].北京:国防工业出版社,1988:190-199.
HAN Kui-ying,WANG Meng-lin,ZHU Su-jun.Atomic mechanism design of gun[M].Beijing: National Defence Industry Press,1988:190-199.(in Chinese)
[5] 戴成勋,靳天佑.朵英贤.自动武器新编[M].北京:国防工业出版社,1990:220-227.
DAI Cheng-xun,JIN Tian-you,DUO Ying-xian.The new works for automatic weapon design[M].Beijing:National Defence Industry Press,1990:220-227.(in Chinese)
[6] 彭峰生,梁世瑞.弹链设计参数协调分析方法研究[J].兵工学报,2004,25(3):272-275.
PENG Feng-sheng,LIANG Shi-rui.A study on ammunition link design by the parameters matching analysis method[J].Acta Armamentarii,2004,25(3):272-275.(in Chinese)
[7] 彭峰生.弹链力学性能研究[J].火炮发射与控制学报,2002(3):25-29.
PENG Feng-sheng.Study on mechanics performance of ammunition link[J].Journal of Gun Launch & Control,2002(3):25-29.(in Chinese)
[8] 王勖成.有限单元法[M].北京:清华大学出版社,2003:666-700.
WANG Xu-cheng.Finite element method[M].Beijing:Tsinghua University Press,2003:666-700.(in Chinese)
[9] 任重.ANSYS实用分析教程[M].北京:北京大学出版社,2003:115-123.
REN Zhong.The practicality analysis tutorial of ANSYS[M].Beijing:Beijing University Press,2003:115-123.(in Chinese).

