基于小波变换信息熵的自动机故障特征提取研究

潘铭志，潘宏侠，任海峰

(中北大学 机械工程与自动化学院，山西 太原 030051)

高速自动机是小口径火炮的核心部件，日益朝着复杂化、高度自动化方向发展，结构日趋精细复杂。因其工作环境为高温高压高冲击，其工作可靠性，其各构件的裂纹及磨损逐渐成为火炮监测与诊断领域关注的焦点。在自动机实射动作中采用现代化的测试与分析手段，监测自动机的运动形态，分析故障产生的原因与机理，通过信号分析与处理识别故障的部分与程度，提出一种能在多干扰、低信噪比的复杂振动信号中，准确、快速提取故障特征并识别故障的方法，是火炮自动机状态监测与诊断领域亟待解决的问题[1]。

信息熵是对信号及系统状态的不确定性的定量评价指标，可以较强的刻画系统内在信息，以及信号特征提取。在机械故障诊断领域，人们尝试使用信息熵方法提取系统运行的内在状态特征。为此，本文在对传统信息熵进行阐述的基础上，进行了用于自动机机箱振动特征信号的信息熵提取方法研究，分析信号在不同的变换空间中的构造信息熵方法，提出不同空间中信息熵提取的模型和算法，并对信息熵模型的参数进行优化。通过理论数据分析及实测信号的分析验证了研究方法的有效性。

1 信息熵提取方法

1.1 小波奇异谱熵(WSE)

小波奇异熵信息测度是融合小波变换、信号的奇异值分解和信息熵提取等相关理论，得到的一种小波信息熵提取方法[2]。

(1)

式中:pi为提取的归一化的奇异特征值;k表示提取的有效奇异特征值的个数，来用于小波奇异熵测度计算。

根据上述定义的小波奇异熵测度，其可以用于将信号从小波空间映射到独立的线性空间，而且可以表达振动响应信号在时频能量分布上的不确定性。通过实现小波奇异熵测度，该测度对于故障产生的暂态信号比较敏感，而且暂态信号的模式越简单，对应的小波奇异熵值越小。因此，适合用小波奇异熵测度来度量被分析故障暂态信号的复杂度和不确定性，而且能够为故障研究提供一个量化和直观的分析结果[3]。

1.2 小波能谱熵(WEE)

首先对信号f(t)进行小波变换，获得小波能谱E，即对有限能量信号f(t)计算其小波变换[4],得到小波能谱熵WEEw,从而可定义为：

(2)

(3)

式中:pi为整个函数能量中尺度i的能量占的比例份额[5]。

由于一维信号通过小波变换等距地映射到二维小波空间，小波函数在频域与时域上，具有一定的支撑区间，此支撑区间具有可自适应变化、速降的特点，小波能谱熵反映了信号在时域与频域上的能量分布特征，同时实现了在尺度空间上对信号能量的划分[6]。

1.3 小波时间熵(WTE)

设在尺度j下，D={d(k),k=1,…,N}为多分辨分析的离散小波系数，在这个小波系数上根据信号特点定义1个滑动窗，设窗宽为w∈N，滑动因子为δ∈N，于是第j尺度下定义的小波时间熵WTE为：

WTEj(m)=-∑pm(Zl)lg(pm(Zl))

(4)

WTEj对机械系统的系统参数或振动信号的变化具有较强的定位和检测能力，由于噪声容易影响j=1尺度分解，在通常的应用中，选取尺度j≥2，本文下一部分的仿真分析中选取j=2，用WTE表示[7]。

2 故障检测仿真实验

建立基于多分辨分析频变系统:

式中:f1=50 Hz;f2=200 Hz;f3=250 Hz;f4=400 Hz。

信号在[0，0.67 s]区间，由50 Hz基波组成，在[0.75 s，1.55 s]区间，由基波与3次谐波构成，在[1.55 s，1.8 s]区间，由基波、3次、5次、7次谐波构成。设定采样频率为1 000 Hz，分析的对象设定为频变信号离散时间序列，选用db4小波，设定移动窗参数w=100，δ=1，计算系统的WEE值、在小波尺度2下WTE值以及WSE值如图1所示[8]。

得出基于多分辨分析频变系统的小波信息熵模型充分利用了对非平稳信号采用小波分析处理时的时频局部化优点，信息熵对信号信息的表征能力得到重要体现，是信号的一种有效特征提取方法[9-10]。

通过对典型模拟信号，频变系统的时间序列进行分析仿真实现，验证了提出的信息熵指标可以定量表征与自动提取信号的多层次特征、不同变换域内的复杂性特征及能量分布特性，并能够有效刻画系统的非线性、非平稳运行特征，因此可以作为系统状态分析和故障诊断的依据。

3 实测信号特征提取

某试验场实测的自动机射击时的振动响应数据如图2所示，图中分别给出了4种工况的时域响应曲线，分别对应于自动机正常，故障1(导气塞漏气)，故障2(转膛滑板裂纹)，故障3(构件出现卡滞)。

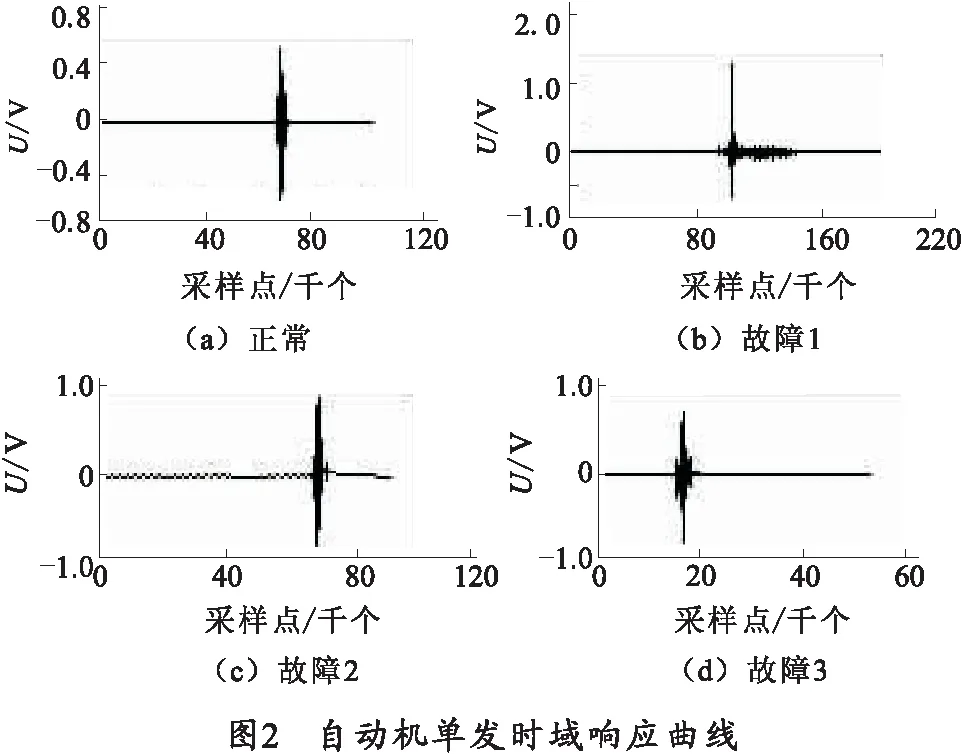
对实测的自动机单发射击时的振动响应数据进行3种信息熵特征提取。

3.1 小波奇异谱熵(WSE)提取

自动机单发振动信号有效长度为550，取窗w=350，滑动因子δ=1，即将信号分为200段，每一段对其采用“db4”小波进行7层小波分解，得到8×350阶的小波系数矩阵，对该矩阵利用奇异值分解理论进行奇异值分解，对提取的有效奇异特征值ESV采用概率分布模型进行谱熵计算，随着窗的移动，便得到自动机机箱单发振动信号的奇异谱熵曲线，如图3所示。

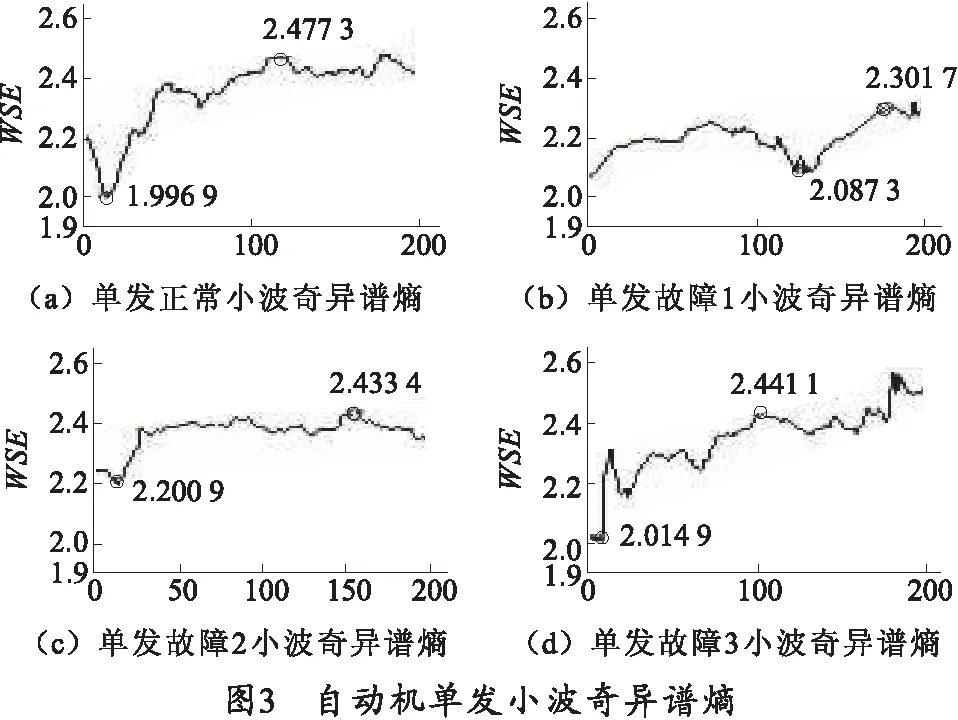
根据上述小波奇异熵测度的提取，该测度可以用于将相关小波空间映射到独立线性空间，可以用于表达被分析信号序列在时频能量分布上的不确定性。单发正常信号的模式与单发故障2、3有一定的相似性，在信号初始段有一定信号频率复杂度畸变，故障2、3信号模式变化较正常信号偏小，因机构卡滞故障3信号频率复杂度变化时间较正常信号早，单发故障1信号模式中间有一段显著减少，故障1信号中间有一段频率复杂度降低。提取各奇异谱熵曲线特征熵值如表1所示。

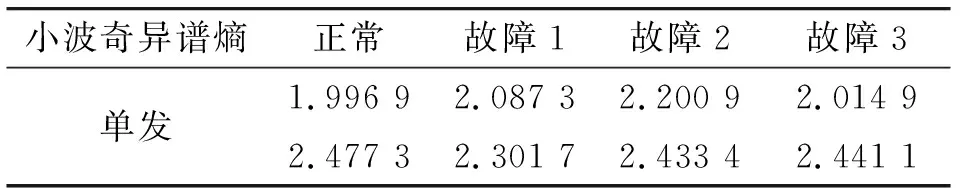
表1 自动机振动小波奇异谱熵

通过奇异熵谱曲线的变化，提取自动机各工况振动信号模式复杂度及不确定性的变化趋势，而且能够为故障研究提供一个直观和量化的分析结果。

3.2 小波能谱熵(WEE)提取

原始单发信号有效长度为550；将信号中设定一滑动窗，窗宽设定为w=150，滑动因子δ=1；随着窗的滑动，可以得到小波能谱熵随时间的变化规律。自动机机箱前测点单发信号，各工况小波能谱熵曲线如图4所示。

从图4可以看出，由于信号在不同尺度下(即不同频带)的信号分布发生改变，各工况小波能谱熵发生显著变化。正常信号小波能谱在初始段有两次畸变，信号能量分布发生两次改变，因为自动机射击过程中复进簧的两次解脱，主动滑板前进带动转膛体碰撞引起；故障1基本没有畸变；因导气塞漏气，其振动响应的能谱变化减弱，小波能谱熵在该设定窗下检测不到能量的改变；故障2信号发生两次突变，是因为转膛滑板裂纹造成与转膛体碰撞过程中响应能量变化减弱，但是突变值极小，其信号频率组成发生非常微弱的变化，滑板裂纹的振动能量分布响应较弱；故障3信号后半程信号能量随小波变化的分布基本没有改变，0～100 之间有一定突变，其突变时间与正常信号小波能谱比较处于两者之间，结构卡滞造成能谱变化时间改变。

取自动机振动小波能谱熵各工况特征突变值如表2所示。

表2 自动机振动小波能谱熵

3.3 小波时间熵(WTE)提取

取自动机机箱前测点单发振动信号，将信号采用“db4”小波在小波分析尺度2下，在此小波系数上定义一滑动窗，设窗宽为w=350，滑动因子为δ=1，即数据信号通过滑动窗被分为200段，在每个滑动窗内，将信号分为10个区间，在区间内通过古典概率论及小波时间熵计算公式，进行各工况自动机机箱振动信号小波时间熵提取,4种工况的单发射击时的小波时间熵如图5所示。

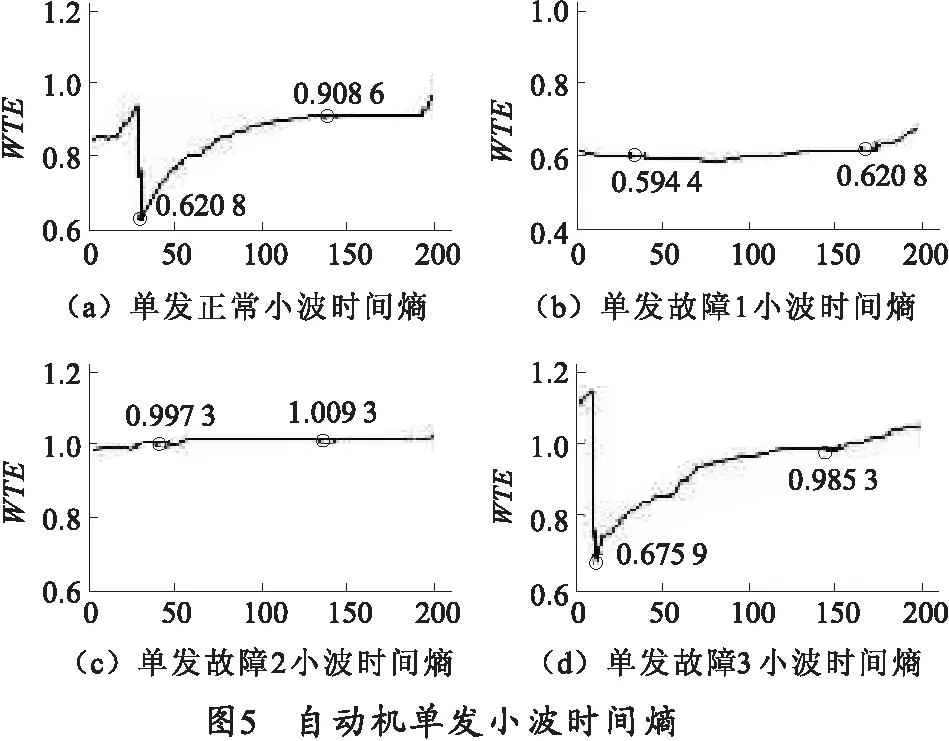
从图5可以看出：自动机单发射击正常及故障3工况的信号初始有一个明显的频变瞬间，小波时间熵有一个明显的奇异变化，故障3与前面小波奇异熵、小波能谱熵类似，因机构卡滞时间稍提前；故障1与故障2信号小波时间熵没有明显的改变，基本趋于平稳，说明因其导气塞故障和滑板裂纹影响，其初始频变不明显，但是其各自的时间熵值具有较大差异，故障2信号时间熵较大，基于经典概率理论，说明故障2信号复杂度高，故障1信号因导气塞漏气故障，信号某段中不同区间落于段中概率变化较小。取自动机振动小波时间熵各工况特征突变值如表3所示。

表3 自动机振动小波时间熵

小波时间熵定量描述了不同故障工况下自动机射击振动的变化规律和非线性状态特征，从而可以作为自动机故障诊断的依据。

4 结 论

本文针对高速自动机的故障诊断提出了小波奇异熵(WSE)，小波能谱熵(WEE)，小波时间熵(WTE)3种信息熵的特征提取方法，并通过对仿真信号与实测自动机单发信号进行分析，验证了本文所提3种方法能够有效表征自动机振动响应状态，在不同工况下具有明显的非线性变化特征，且其变化规律和具体形式随系统故障状态和程度的不同而有所不同。上述3种特征指标能够有效反映自动机运行状态，可以用于自动机振动信号故障特征提取。

[1] 王茂林，张国平．GA35自动机机构设计创新思想分析[J]．火炮发射与控制学报，2005(3)：28-31．

WANG Mao-lin，ZHANG Guo-ping．Analysis of innovatory thought for structure design of GA35 automatic gun [J]．Journal of Gun Launch & Control，2005(3)：28-31．(in Chinese)

[2] 吴定海，张培林，张英堂，等．基于时频奇异谱的柴油机缸盖振动信号特征提取研究[J]．振动与冲击，2010，29(9)：221-224．

WU Ding-hai，ZHANG Pei-lin，ZHANG Ying-tang，et al．Based on the singular spectrum of diesel engine cylinder head vibration signal feature extraction [J]．Vibration and Shork，2010，29(9)：221-224．(in Chinese)

[3] 何正友，蔡玉梅，钱清泉．小波熵理论及其在电力系统故障检测中的应用研究[J]．中国电机工程学报，2005，25(5)：39-43．

HE Zheng-you，CAI Yu-mei，QIAN Qing-quan．Wavelet entropy theory and its application in electric power system fault detection[J]．Chinese Journal of Mechanical Engineering，2005，25(5)：39-43．(in Chinese)

[4] HUANG Jian，HU Xiao-guang，GENG Xin．An intelligent fault diagnosis method of high voltage circuit breaker based on improved EMD energy entropy and multi-class support vector machine[J]．Electric Power Systems Research,2011,81(2):400-407．

[5] 吕勇，李友荣，王志刚．一种弱故障特征信号的提取方法及其应用研究[J]．振动工程学报，2007，20(1)：24-28．

LV Yong，LI You-rong，WANG Zhi-gang．A weak fault signal extraction method and its application [J]．Journal of Vibration Engineering，2007，20(1)：24-28．(in Chinese)

[6] 谢平．故障诊断中信息熵特征提取及融合方法研究[D]．秦皇岛：燕山大学，2006．

XIE Ping．Staty on information entropy feature extraction and fusion methods in fault diagnosis[D]．Qinhuangdao：Yanshan University，2006．(in Chinese)

[7] 桂中华，韩凤琴，张浩．小波包特征嫡提取水轮机尾水管动态特性信息[J]．电力系统自动化，2004，28(13)：13-17．

GUI Zhong-hua，HAN Feng-qin，ZHANG Hao．Wavelet packet entropy feature extraction turbine dynamic characteristic information[J]．Automation of Electric Power Systems，2004，28(13)：13-17．(in Chinese)

[8] ENDO H，RANDALL R B．Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J]．Mechanical Systems and Signal Processing,2007,21(2):906-919．

[9] 卢晓莉，罗键．信息融合熵在机械故障诊断中的应用[J]．厦门大学学报，2006，45(1)：39-43．

LU Xiao-li，LUO Jian．Information fusion in fault diagnosis of machinery[J]．Journal of Xiamen University，2006，45(1)：39-43．(in Chinese)

[10] 潘铭志，潘宏侠，赵润鹏．自动机机箱振动分析与诊断研究[J]．火炮发射与控制学报，2012(2)：67-70．

PAN Ming-zhi，PAN Hong-xia，ZHAO Run-peng．Automatic receiver vibration analysis and diagnosis research[J]．Journal of Gun Launch & Control，2012(2)：67-70．(in Chinese)