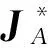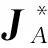秩为n-1的n阶矩阵的伴随矩阵的Jordan标准形

侯晓丽，周永安

(郑州轻工业学院 数学与信息科学系， 河南 郑州 450002)

众所周知，任意方阵A都有Jordan标准形，它是与A相似的形式最简单的矩阵.其中，对角矩阵是特殊的Jordan矩阵，但能与对角矩阵相似的矩阵只有正规矩阵[1-3].一个矩阵A的Jordan标准形堪称一张名片，有了它就可以很容易地知道其行列式是多少、是否可逆、每一个特征值的代数重数和几何重数及指标各是多少，以及它的最小多项式形式和初等因子、行列式因子、不变因子等情形.文献[4]把矩阵的Jordan标准形应用于矩阵函数的研究和简化Hamilton-Caylay定理的证明，文献[5]把矩阵的Jordan标准形分解推广到四元数矩阵的情形等.本研究限于讨论R(A)=n-1的情形下，A的Jordan标准形的情况，并约定以Cn×n，A*,JA，Eij分别表示复数域上全体n阶方阵的集合、方阵A的伴随矩阵和Jordan标准形以及(i,j)元素是1其余元素全为0的n阶矩阵.

1 相关概念及性质

定义主对角线上的小块方阵Ji(a)是Jordan块的n阶准对角矩阵

(1)

其中，n=m1+m2+…+ms，称为Jordan形矩阵.

引理1每个n级的复数矩阵A都与一个Jordan形矩阵相似，这个Jordan形矩阵除去其中Jordan块的排列次序外由矩阵A唯一决定，它称为A的Jordan标准形.

引理2设A为n阶方阵，则存在n阶可逆矩阵P，使

P-1AP=JA，P*A*(P-1)*=JA*.

(2)

2 关于伴随矩阵的Jordan标准形的结果

定理1设A∈Cn×n，R(A)=n-1，a1a2…as…an-1≠0,则

(a)当A仅有一个零特征值时，将其置于JA的最后一个位置，有

(3)

(b) 当A有两个或两个以上零特征值时，其几何重数必为1，且

(4)

其中，δ非0即1.

证明仅证(b).

反证，设A的零特征值的几何重数大于1，为了证明简单起见，设A的零特征值的几何重数为2.

一方面，因R(A)=n-1，那么R(JA)=n-1.

s+[(n-s)-2]=n-2

这与R(JA)=n-1矛盾.

(5)

(b)当A的零特征值的代数重数大于1时，

(6)

证明(a)显然.

(b)由于A的零特征值的代数重数大于1，根据定理1，此零特征值的几何重数为1.于是

观察此JA的表达式，不难看出JA中的(n，s+1)元的代数余子式为

(7)

(1) 当s=n-1时，

(2) 当1≤s≤n-2时，取

其中，ei为第i个n维单位坐标向量，则

上式中，前面是s个0，后面是(n-s-2)个0.

参考文献：

[1]于寅.高等工程数学[M].武汉：华中科技大学出版社,2001：82.

[2]陈公宁.矩阵理论及其应用[M].2版.北京:科学出版社,2007:30.

[3]王卿文.高等数学综论[M].香港:香港天马图书有限公司,2000:129.

[4]王英.若尔当标准形问题新探[J].湖南理工学院学报:自然科学版，2007,20(1)：17-19.

[5]陈龙玄,侯仁民,王亮涛.四元数矩阵的Jordan标准形[J].应用数学和力学,1996,17(6)：533-542.