仅有一个平衡点的超混沌系统的控制与同步

胥红星

(郑州航空工业管理学院 工业管理学院, 河南 郑州 450046)

目前，关于混沌的研究已经发展成为一个应用广泛的研究领域，在物理、化学、生物学等学科得到了广泛的应用，许多新的混沌模型不断被发现，如著名的Chen系统[1]、Lü系统[2]等.

最初，人们认为实现混沌系统的控制和同步是不可能的.1990年，Grebogi和Yorke提出的控制混沌思想产生了广泛的影响[3].同年，Pecora和Carroll提出了混沌同步的思想[4].随后，人们提出了各种控制混沌的方法,如线性与非线性反馈控制[5]、自适应反馈控制[6-7]等，并作了大量实验验证.文献[8]基于Lü系统提出了一个新混沌模型，仅有一个平衡点，但具有两个正的Lyapunov指数，表现出更为复杂的动力学行为，是个典型的超混沌系统.本研究根据系统本身的特性，进一步分析了该系统的动力学行为，采用线性反馈法把其镇定到不稳定的平衡点.利用非线性反馈法实现了该系统的同步性，数值仿真验证了理论的可行性.

1 混沌模型及性质分析

混沌模型描述如下:

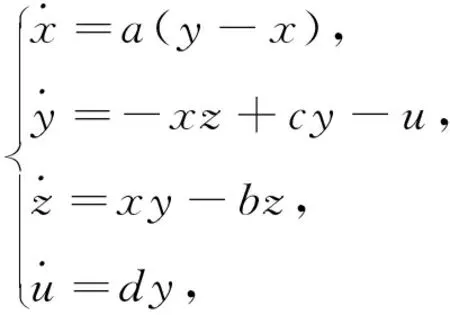
(1)

其中，x，y，z，u为状态变量，当a+b>c时，系统是耗散的且系统仅有一个平衡点O(0，0，0，0),取a=36，b=3，c=26，d=10时，系统存在典型的超混沌吸引子,如图1所示.当a=36，b=3，c=26时，随着参数d的变化，系统产生超混沌，混沌，周期，倍周期动力学行为，d∈[0，50]系统(1)的Lyapunov指数谱如图2所示.

图1 混沌系统的吸引子

图2 d∈[0，50]系统(1)的Lyapunov指数

2 系统(1)的控制问题

限定参数大于0，由于系统(1)有且仅有一个平衡点，利用线性反馈法设计合理的控制器实现平衡点O(0，0，0，0)的控制.

设受控系统如下：

(2)

其中，v1，v2，v3，v4为控制器.

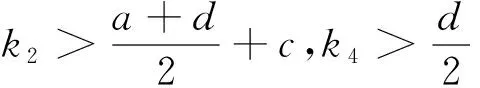
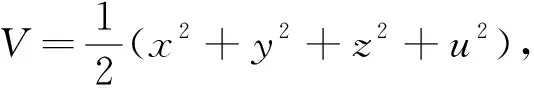
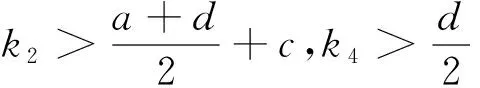
3 混沌系统的同步

定义1对于两个非线性混沌系统：

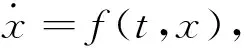
(3)

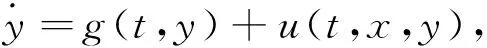
(4)

令(1)为驱动系统，响应系统为

(5)

令e(t)=(e1，e2，e3，e4)T=(x1-x，y1-y，z1-z，u1-u)T，则误差系统为:

(6)

其中，vi(t)为反馈控制器，i=1，2，3，4.

定理2对系统(6), 选取如下控制器：

(1)v1(t)=ze2-ye3，v2(t)=-k2e2，v3(t)=0，v4(t)=-k4e4；

(2)v1(t)=ze2，v2(t)=-k2e2，v3(t)=ye1，v4(t)=-k4e4.

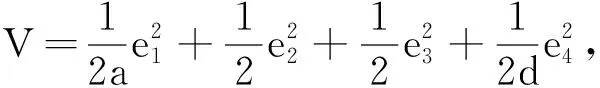
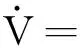
类似可证在控制器(2)下系统的同步性成立.

4 数值仿真

用Matlab进行数值仿真，设初值点为(0.1,0.3,0.5,0.2)，根据定理1，取反馈增益k2=44，k4=11,得到相空间的稳定轨迹，如图3所示.根据定理2，取反馈系数k2=21，k4=1，则系统(1)和系统(5)是全局同步的，如图4所示，可以看出设计控制器的有效性.

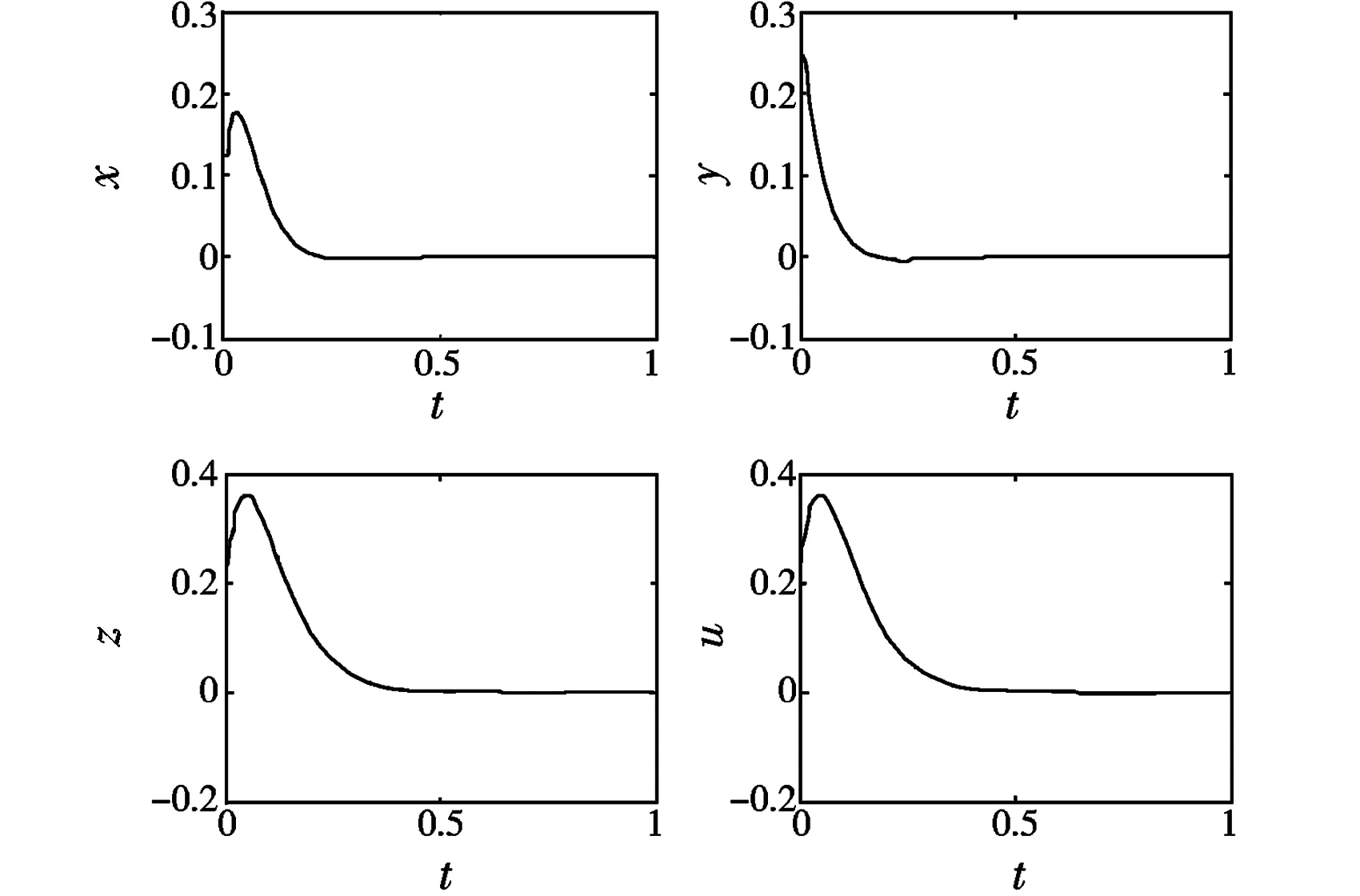
图3 线性反馈下系统(1)的状态曲线

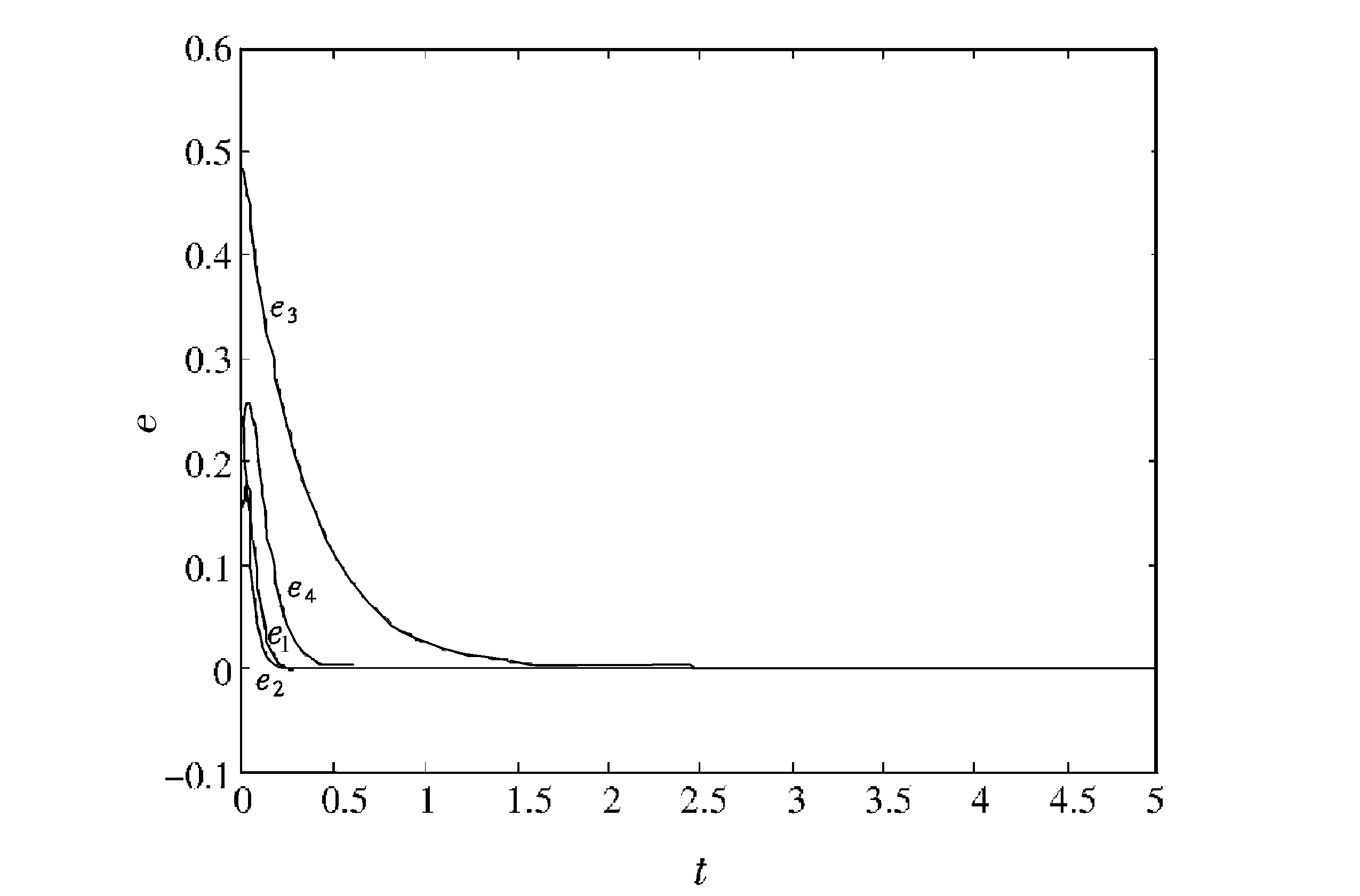
图4 非线性反馈下的同步误差

5 结论

研究了仅有一个平衡点的超混沌的控制和同步问题，利用线性反馈方法把系统镇定到平衡点，设计了非线性反馈控制器实现了系统的全局同步，数值仿真验证了控制器的有效性.

参考文献：

[1]Lorenz E.Deterministic non-periods flows[J].J Atmos Science,1963,20(3):130-141.

[2]Chen G,Ueta G T.Yet another chaotic attractor[J].Int J Bifurcat Chaos,1999,9(7):1465-1466.

[3]Lü J,Chen G.A new chaotic attractor coined[J].Int J Bifurcat Chaos,2002,12(3):659-661.

[4]Ott E,Grebog I C,York J.Cont rolling chaos[J].Physical Review Letters,1990,64(11):1196-1199.

[5]Pecora L M,Carroll T L.Synchronization in chaotic systems[J].Phys Rev Letters,1990,64(8):821-824.

[6]Yassen M T.Cont rolling chaos and synchronization for new chaotic system using linear feedback control[J].Chaos Solitons & Fractals,2005,26(3):913-920.

[7]Wu X Y,Guan Z H,Wu Z P.Adaptive synchronization between two different hyperchaotic systems[J].Nonlinear Analysis,2008(13):46- 51.

[8]Shen Q K,Zhang T P.Novel design of adaptive neural network controller for a class of non-affine nonlinear systems[J].Commun Nonlinear Sci Numer Simulat,2012,17(3):1107-1116.

[9]Jia H Y,Chen Z Q,Yuan Z Z.A novel one equilibrium hyper-chaotic system generated upon Lu attractor[J].Chin Phys B,2010,19(2):5-7.