空间圆的参数方程及其应用罗治国

罗治国

(湖南师范大学数学与计算机科学学院，中国 长沙 410081)

当球面与平面相交时，其交线是圆. 反之，空间的任何圆都可以表示成为一个球面与一个平面的交线. 所以，空间圆的直角坐标方程为[1-3]

或

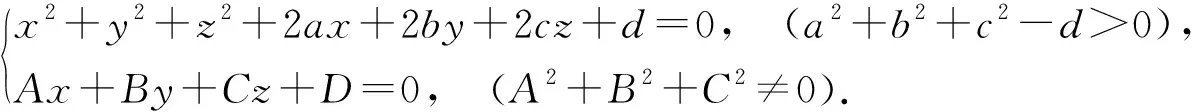
本文首先利用直角坐标变换给出了空间圆的参数方程，然后给出了空间任意方向圆柱面和圆锥面的参数方程，并用例子说明结论的正确性.

1 空间圆的参数方程

命题1圆心在原点，半径为r，位于平面

cosαx+cosβy+cosγz=0, cos2α+cos2β+cos2γ=1,cosγ≠1

上的圆的参数方程可以写为

(1)

圆心在原点、半径为r、位于平面z=0上的圆的参数方程可以写为：

x=rcosθ,y=rsinθ,z=0,0≤θ≤2π.

证只需证明命题的前半部分，以平面cosαx+cosβy+cosγz=0作为新坐标系Ox′y′z′的Ox′y′平面作旋转变换

由于圆心在原点、半径为r、位于平面Ox′y′上的圆的参数方程可以写为

x′=rcosθ,y′=rsinθ,z′=0,0≤θ≤2π.

所以，所求圆的参数方程为(1). 证毕.

注简单计算即知(1)满足方程

所以，它表示给定条件的圆.

推论1圆心为(x0,y0,z0)，半径为r，位于平面

A(x-x0)+B(y-y0)+C(z-z0)=0,A2+B2≠0

上的圆的参数方程可以写为：

圆心为(x0,y0,z0)，半径为r，位于平面z=z0上的圆的参数方程可以写为[2]：

x=x0+rcosθ,y=y0+rsinθ,z=z0,0≤θ≤2π.

2 应用

首先，利用上面给出的空间圆的参数方程，容易得到空间任意方向圆柱面的参数方程.

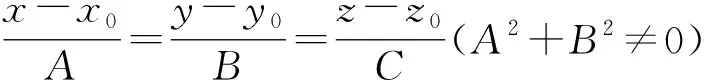
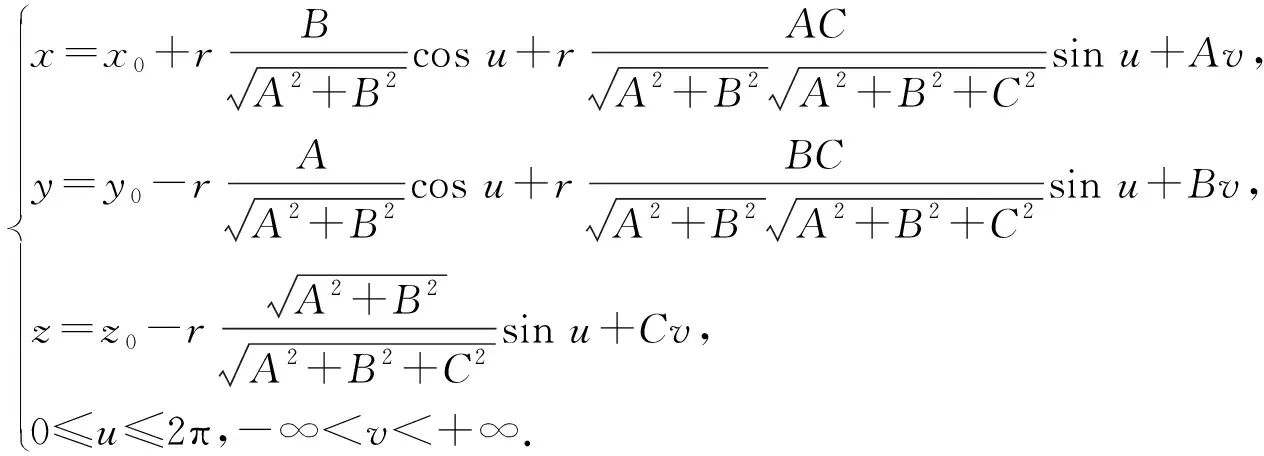
利用上面的方法容易得到

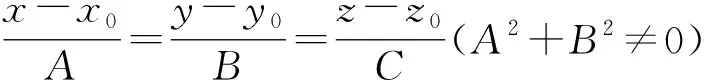
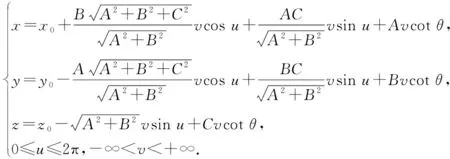
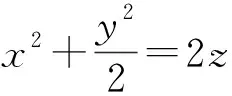
解由题设知圆心在平面y=0上. 可设圆的参数方程为

所以

参考文献：

[1] 李养成，郭瑞芝.空间解析几何[M].北京：科学出版社，2004.

[2] 朱鼎勋，陈绍菱.空间解析几何学[M].北京：北京师范大学出版社，1984.

[3] 王兴波.空间任意方向圆柱面的参数方程[J].佛山科学技术学院学报:自然科学版, 2010,28(6):58-63.

[4] 动网论坛.三维空间中圆的参数方程[EB/OL]. http://www.mathchina.net/dvbbs/ dispbbs. asp?boardid=3&Id=471, 2010-09-06.

[5] CSDN论坛.关于空间中圆的方程和参数方程[EB/OL]. http://topic.csdn.net/t/ 20050302/ 15/3818707.html, 2005-03-02.

[6] 百度知道>教育/科学>理工学科>数学, 要求出一个空间圆的参数方程，知道平面方程ax+by+cz+d=0, 知道球的方程(x-x0)2+(y-y0)2+(z-z0)2=r2[EB/OL]. http:// zhidao. baidu. com/question/292455694.html, 2011-07-14.

[7] 数学中国.知道圆心和半径以及法向量，空间圆参数方程怎么得到[EB/OL]. http://bbs. mathchina.com/cgi-bin/topic.cgi?forum=4&topic=1744&show=100, 2010-01-20.

[8] 百度知道>电脑/网络>百度. 空间圆的参数方程，要求所在平面为空间内任意平面[EB/OL].http://zhidao.baidu.com/question/213093435.html?pt=360se.?zid=10081, 2011-01- 06.

[9] 李养成.空间解析几何[M].北京：科学出版社，2007.