KdV方程的双Wronskian解研究艾玉波

艾玉波

(连云港师范高等专科学校 数学与应用数学系,中国 连云港 222006)

孤立子理论是应用数学和数学物理的一个重要组成部分，近几十年受到国际数学界和物理界的普遍重视．孤立子往往也称为孤立波[1]，它是指一大类非线性偏微分方程的具有特殊性质的解，及与之相应的物理现象．随着研究的深入，大批具有孤立子解的非线性波动方程在各个领域不断被揭示，寻求孤子方程的精确解以及讨论解的性质成为孤立子方程研究中的重大课题．

1 修正KdV方程Hirota形式的n孤子解

于是双孤子解为

再根据截断式的求解方法，令：

修正KdV方程的n孤子解为

2 修正KdV方程双Wronskian形式的有理解

为了能够求解KdV方程的双Wronskian解，首先要计算等谱AKNS方程族中的三阶AKNS方程[5-7]．

根据等谱AKNS方程组

将推算因子L代入方程组得

对方程组进行等谱变换为

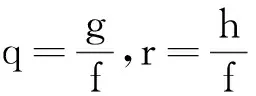
gtf-gft+gxxxf-3gxxfx+3gxfxx-gfxxx=0.

利用多项式解对导数方程进行分解得到

因此原双Wronskian行列式的有理解为

3 修正KdV方程的双Wronskian解[8-11]

利用线性导数方程求上述导数方程得有理解，本文不再赘述，由于借助系数矩阵的正定表达式化简了修正KdV方程组的一阶常微分方程，因此对于改进的KdV方程的双Wronskian解可以不考虑复特征根的情况，从而只计算其有理解．

当N=0时，对于实根导数方程可以得到

则g与f的商为修正KdV方程的单孤子解．

当N=1时，实根导数方程有：

φ1=c0e4λ3t-λx,φ2=c0(-x+12λ2t+1)e4λ3t-λx,

φ1=d0e-4λ3t+λx,φ2=d0(x-12λ2t+1)e-4λ3t+λx,

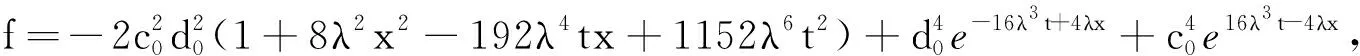
g= 8c0d03(-24λ4t+ 2λ2x-λ)e-8λ3t + 2λx+ 8c03d0(-24λ4t+λ2x+λ)e8λ3t-2λx.

则g与f的商为修正KdV方程的双孤子解．

4 KdV-mKdV混合方程的双线性形式及其孤子解

命ut+6uux+6u2ux+uxxx=0为KdV-mKdV混合方程[12]．

函数f(t,x)与g(t,x)的双线性导数定义为

对上述作变换

其中ω*是复函数ω的共扼函数;α取任意常数．

将变换代入ut+6uux+6u2ux+uxxx=0，则KdV-mKdV混合方程变为

故方程的双线性导数方程为

5 结论

本文研究了修正KdV方程Hirota形式的n孤子解，给出了修正KdV方程双Wronskian形式的有理解及修正KdV方程的Wronskian解.利用双线性导数法所给出的修正KdV方程的n孤子解是一个复杂的和式，将它代入方程验证，利用线性导数方程的列向量计算了修正KdV方程的双Wronskian解．

参考文献：

[1] 谷超豪．孤立子理论与应用[M].杭州：浙江科技出版社， 1990.

[2] 谷超豪，胡和生，周子翔．孤子理论中的达布变换及其几何应用[M].上海：上海科技出版社， 2005．

[3] FREEMAN N C, NIMMO J J C. Soliton solutions of the KdV and KP equations：the Wronskian technique[J]. Math Phys Eng Sci, 1983,389(1797):319-329．

[4] 何进春，黄念宁.关于KdV方程孤子解的研究[J].应用数学， 2007，20(1):145-150.

[5] HIROTA R, YOHTA , SATSUMA J. Solutions of the KP equation and the two-dimensional Toda equation[J]. J Phys Soc Japan, 2011,57(8):1901-1904．

[6] 陈登远. Backlund变换与n孤子解[J].数学研究与评论, 2005,25(3):479-488.

[7] NIMMO J J C, FREEMAN N C. A method of obtaining the N-soliton solution of the Boussinesq equation in term of a wronskian [J]. Phys Lett A, 1983,95(1):4-6.

[8] 吕丽丽,郝洪海,毕金钵,等.修正KdV方程的双Wronskian解[J].上海大学学报:自然科学版, 2006,12(4):383-388.

[9] 王艳红，王世勋. 一类KdV方程的精确解[J].信阳师范学院学报， 2010，23(4):492-495.

[10] 何亿捷．KdV方程纯孤立子解的整体渐进性质[J]．数学年刊, 2009,30A(5):659-668.

[11] 张大军,邓淑芳.孤子解的Wronskian表示[J].上海大学学报:自然科学版, 2002,8(3):232-242.

[12] 吴妙仙，王晓芳，张 翼.Hirota方法求解KdV-mKdV混合方程的多孤子解[J].浙江教育学院学报, 2008,3(2):69-74.