具有区间支付的合作对策的区间强ε-核心

邹正兴,高作峰

(燕山大学理学院,河北 秦皇岛 066004)

核心是经典合作对策常用的集合形式的解.生活中处处充满着不确定性,经典合作对策的理论将不再适用,具有不确定性收益的模糊合作对策引起了人们的关注.Hinojosa等[1]讨论了包含多种状态的合作对策的核心、最小核心、核仁,引入了P-核心的概念.Branzei R等[2]建立了具有区间收益的模糊合作对策模型,为区间合作对策的研究奠定了基础.Alparslan Gok等[3-4]改进了区间合作对策模型,对经典合作对策的分配、核心、优超核心进行了拓展,并研究了区间合作对策的一些性质.于晓辉等[5]重新定义了模糊支付合作对策的模糊核心,给出了该模糊核心的存在条件,探讨了模糊核心与模糊Shapley 值的关系.本文中在Alparslan Gok建立的区间合作对策模型的基础上,结合经典合作对策核心[6-8]的相关理论,定义了区间合作对策的区间强ε-核心、区间P-核心、区间最小核心、区间最小P-核心,并尝试着研究这些核心的一些特征和性质.

1 基本概念和记号

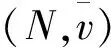
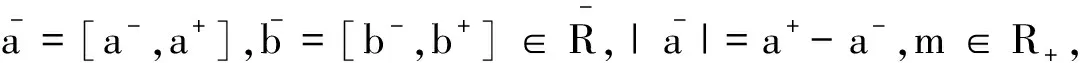
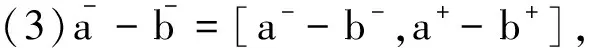
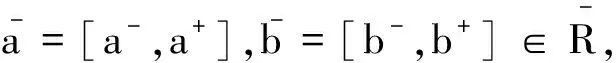
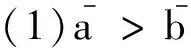
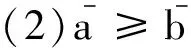
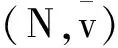
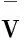
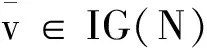
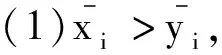
则称x关于S优超y,记为xdomSy.对于任意两个分配,如果存在一个非空联盟S,使得xdomSy,则称x优超y.

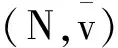
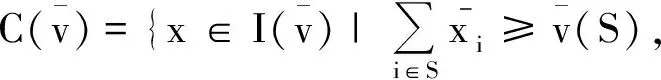
(1)

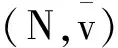
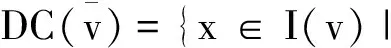
(2)

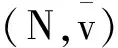
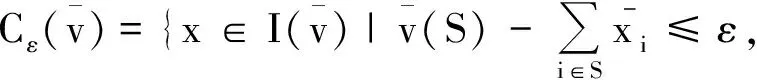
(3)

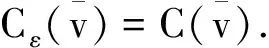
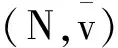
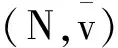
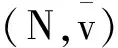
2 主要结论

2.1 相关性质及证明

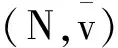
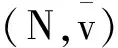
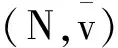
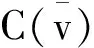
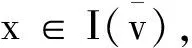
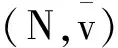
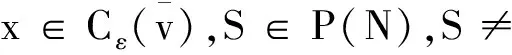
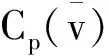
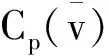
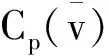
类似地,可以证明(2)、(3).证毕.

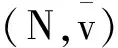
定理5证明先证ε0=max{p01,p02}.

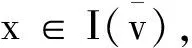
2.2求区间核心中的分配区间核心为区间合作对策集合形式的解,求解起来比较困难,但我们可以通过数学规划的方法求出处于区间核心中的某一分配.求区间核心中分配的主问题可以描述为：

minw-+w+

(5)

(6)

使得

(7)

(8)

(9)

xi-≤xi+,i∈N

(10)

xi-,xi+∈R

(11)

w-,w+≥0

(12)

在上述数学规划问题中,约束条件(6)～(9)表明分配的有效性与合理性,约束条件(10)表明区间数的合理性.求解该问题的算法如下：

步骤1：给出初始联盟集Ω,例如Ω={{1},{2},…,{n}}.

步骤2：求出最优化问题(5)～(12)的最优解.

步骤3：如果w-+w+>0,则算法停止.此时区间核心为空.

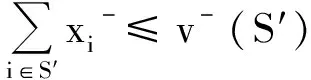
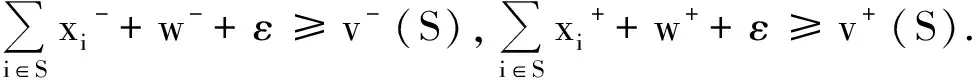
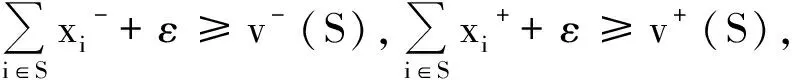
类似地,可以求出区间P-核心、区间最小P-核心中的某一分配.

3 结论

以区间数的运算为主要工具,结合经典合作对策的相关定义及性质,定义了区间合作对策的区间强ε-核心、区间P-核心、区间最小核心、区间最小P-核心,尝试着研究这些核心的一些特征和性质,并设计了一种可行的方法求出处于区间核心中的某一分配,对区间合作对策的理论研究以及相关的应用有一定的参考价值.区间核心具有较强的应用性,但区间核心通常是集合形式的解,如何限定从区间核心中取出的元素使其更具说服力将是以后的研究重点.

[1] Hinojosa M A, Marmol A M, Thomas L C. Core, least core and nucleolus for multiple scenario cooperative games[J]. European Journal of Operational Research, 2005, 164(1)：225-238.

[2] Branzei R, Dimitrov D, Tijs S. Shapley-like values for interval bankruptcy games[J]. Economics Bulletin, 2003(3):1-8.

[3] Alparslan Gok S Z,Miquel S,Tijs S.Cooperation under interval uncertainty[J]. Mathematical Methods of Operations Research, 2009, 69(1):99-109.

[4] Alparslan Gok S Z, Branzei O, Branzei R,et al. Set-valued solution concepts using interval-type payoffs for interval games[J]. Journal of Mathematical Economics, 2011, 47(4/5):621-626.

[5] 于晓辉, 张强. 模糊支付合作对策的核心及其在收益分配问题中的应用[J].模糊系统与数学,2010,24(6):66-75.

[6] Peters H. Game Theory—a multi-leveled approach[M].Berlin Heidelberg：Springer-Verlag, 2008：229-232.

[7] Branzei R, Dimitrov D, Tijs S.Models in cooperative game theory[M]. Berlin Heidelberg：Springer-Verlag, 2008：13-25.

[8] 高作峰,王友,王国成.对策理论与经济管理决策[M]. 北京:中国林业出版社, 2006：60-77.

[9] Julia Drechsel. Cooperative lot sizing games in supply chains[M]. Berlin Heidelberg：Springer-Verlag, 2010：81-85.