开关磁阻电机神经网络非线性映射建模方法研究

宋受俊，张 蔓，尹文财，李 岩

(西北工业大学，陕西西安710072)

0 引 言

起动转矩大、调速范围宽、控制灵活、适应恶劣环境以及成本较低等优良性能使开关磁阻电机(以下简称SRM)具备了与交流电机、直流电机以及无刷直流电机相竞争的潜在优势［1］，在多电飞机［2］、电动汽车［3］、风力发电［4］等军民用领域具有广阔的应用空间和巨大的发展潜力。

然而，绕组电流的非正弦性以及铁心磁密的高饱和性使SRM 驱动系统成为了一个多变量、强耦合的非线性系统，给建模仿真带来了较大的困难。建立准确、高效的仿真模型一直是SRM 研究中的热点和难点。至今，国内外学者已提出多种建模方法，大致可分为解析法、数值法和映射法三类。解析法通过分段线性化、多项式拟合、等效磁网络等技术得到描述电磁特性的解析式，进而建立SRM 仿真模型［5－6］，该方法仿真速度快、数据量小，便于工程实现，但各种假设及简化的引入大大降低了模型精度，且对使用者的专业化水平要求较高。数值法直接利用二维或三维有限元技术得到SRM 的动、静态特性，该方法的准确性较高，但处理过程繁琐，计算时间长，数据量大，且仅适用于电机性能计算，无法实现SRM 驱动系统实时控制的仿真需求［7－8］。映射法大多将电机的电磁特性以查询表、神经网络等形式存储，直接建立输入和输出变量间的映射关系，避免了仿真时非线性插值所需的大量运算，提高了仿真速度，且只要保证训练数据源的准确性，就可以得到准确的电机模型［9－10］。

本文将数值法和映射法相结合，使它们优势互补，首先利用有限元法对一个四相8 /6 极SRM 样机进行了分析，得到了该样机的磁化及转矩特性数据。然后，利用这些数据分别对反向传播神经网络(BPNN)和径向基函数神经网络(RBFNN)进行了训练，建立了SRM 驱动系统的非线性模型。最后，在角度位置、电流斩波等不同的控制方式下，将所建立模型的仿真结果与有限元方法进行了对比，证明了所建立模型的有效性。另外，对神经网络的结构及训练参数进行了敏感性分析，为减小网络规模，提高逼近及泛化能力提供了依据。

1 SRM 基本方程

开关磁阻电机的运行遵循基本的电磁规律，假设各相结构和电磁参数对称，不计磁滞、涡流及绕组互感，根据电路基本定律，可以写出SRM 第k 相的电压平衡方程:

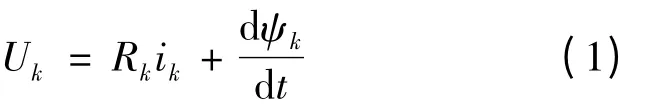
式中:Uk、Rk、ik及ψk分别为第k 相绕组的端电压、相电阻、相电

流和磁链。

磁链ψk是绕组电流ik和转子位置角θ 的非线性函数，称为磁化特性，可用电感和电流的乘积表示，即:

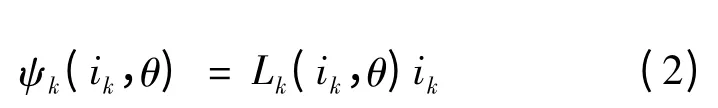
将式(2)代入式(1)可得:

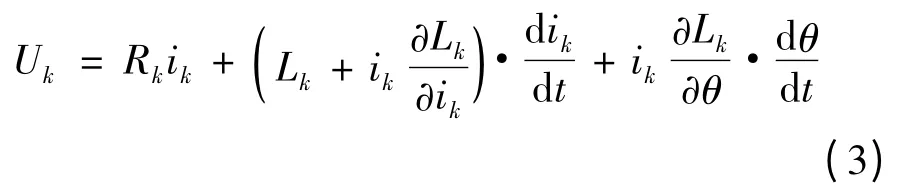
电源电压与电路中三部分电压降相平衡:等式右端第一项为回路中的电阻压降;第二项为变压器电动势，是由电流变化引起磁链变化而感应的电动势;第三项称为运动电动势，是由转子位置改变引起磁链变化而感应的电动势。

每相绕组所产生的电磁转矩Tk是相电流与转子位置角的非线性函数，称为转矩特性，需要根据磁储能或磁共能W′k来计算，即:

忽略互感影响，总的电磁转矩为各相转矩之和:

根据力学原理，电机转子机械运动方程:

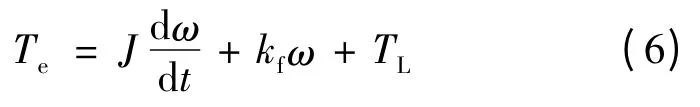
式中:J 为SRM 的转动惯量;ω 为转子机械角速度;kf为摩擦系数;TL为负载转矩。

上述基本方程式是建立SRM 驱动系统仿真模型的基础，其中，准确且高效地描述磁化特性ψk(ik，θ)以及转矩特性Tk(ik，θ)是建模的关键。

2 有限元分析

样本数据是否能够准确反映所研究对象的特性是神经网络建模的关键，考虑到数值建模法准确性高的优点，本文首先通过有限元分析，得到了SRM样机的磁化及转矩特性数据，作为神经网络训练的样本。

图1 为SRM 样机的二维有限元模型，为了缩短求解时间，根据对称原理，只使用了半个电机进行仿真。表1 给出了所研究SRM 样机的主要参数。

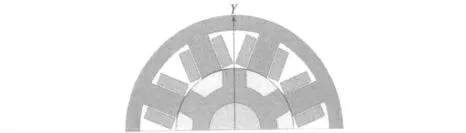
图1 SRM 样机二维有限元模型

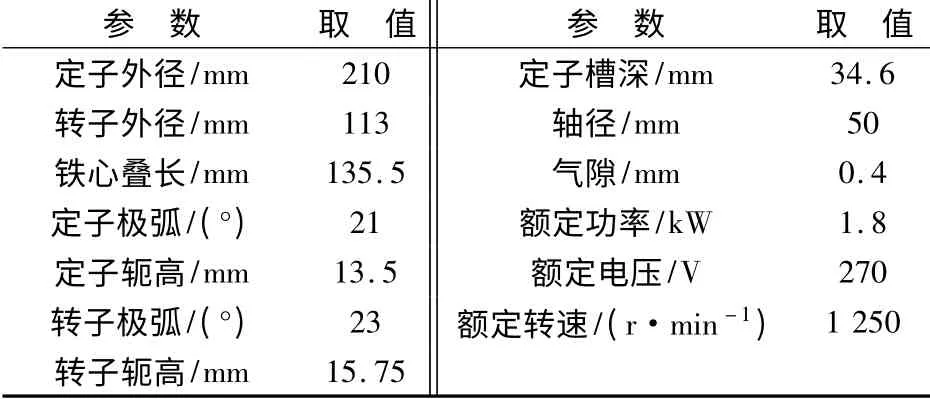
表1 SRM 样机主要参数

经过赋予材料、边界设定、剖分以及参数化求解等步骤，可以得到电机的磁化及转矩特性数据。充分利用SRM 各相独立和结构的对称性，可以极大地减少样本数据的准备工作，降低神经网络的复杂度，节约计算时间和内存开销。图2 给出了磁化特性数据，相电流参数化范围为0～20 A，间距为1 A，转子位置角的参数化范围为0°～30°，间距为3°。图3为转矩特性数据，相电流参数化范围为0～20 A，间距为2 A，转子位置角的参数化范围为0°～30°，间距为1°。

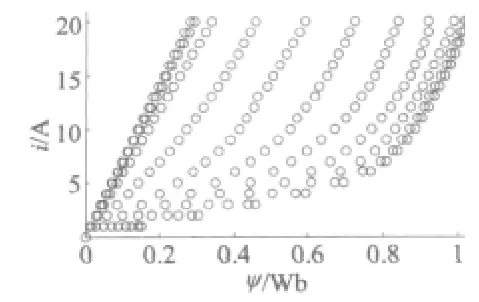
图2 磁化特性数据

图3 转矩特性数据

3 神经网络训练

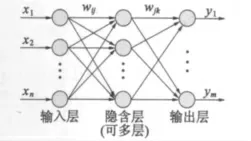
通过前期对各种典型神经网络的比较分析，本文选用了BP 神经网络和RBF 神经网络。BP 神经网络是一种误差逆传播训练的多层前馈网络，它采用最速下降法进行学习，通过误差反向传播不断调整网络的权值和阈值，使网络的误差平方和最小。RBF 神经网络是一种三层前向网络，它用径向基函数作为隐单元的“基”构成隐含层空间，对输入矢量进行一次变换，将低维的输入数据直接映射到高维隐空间，无需权连接，通过对隐单元的加权求和得到输出。除训练思想不同外，上述两种神经网络具有相似的拓扑结构，图4 给出了BP 神经网络的拓扑结构图。需要说明的是，BPNN 可以具有多个隐含层，而RBFNN只有一个隐含层，并且其输入层与隐含层间的连接权值为1。

上述两种神经网络的训练过程大致相同，本文以BP 神经网络为例进行说明。BP 神经网络中的可变参数主要有学习速率、目标误差、隐含层数以及节点数等，它们对于网络的性能具有很大的影响，有必要通过敏感性分析优化其取值。以转矩特性为例，将样本数据分为两部分，电流为{0，4 A，8 A，12 A，16 A，20 A}的数据称为“训练及逼近数据”，用来对BP 网络进行训练，同时也用来验证训练后网络的逼近能力;而电流为{2 A，6 A，10 A，14 A，18 A}的数据称为“泛化数据”，主要用来测试训练后网络的泛化能力。这样分类不仅保证了用于训练的样本集合覆盖整个工作区域，且分布均匀，数据充分。

图5～图7 给出了不同训练参数下BP 神经网络的性能，包括逼近和泛化检验。图中以“* ”表示的是有限元分析得到的数据，曲线为BPNN 的输出。表2 给出了三种情况下的参数取值。

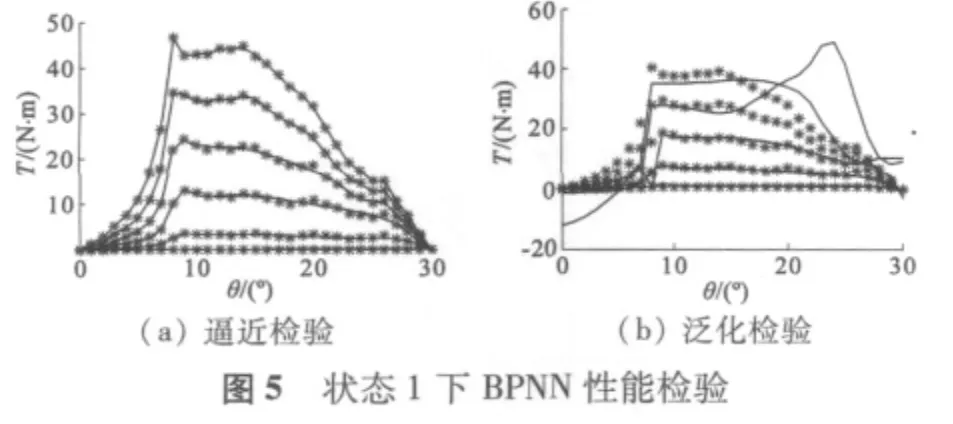
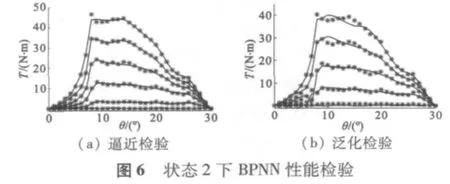
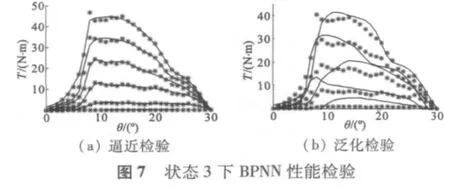
表2 BP 神经网络敏感性分析训练参数

状态1 的学习速率比状态2 小，由以上两图可见，随着学习速率的减小，网络的逼近能力有所提高，但泛化能力会大幅下降。这是因为学习速率较小时，所需训练时间较长，出现“过学习”现象，不能很好地“举一反三”，使得泛化能力下降。学习速率也不宜过大，否则会出现“欠学习”现象，不能保证训练精度，甚至引起振荡。

状态3 的目标误差比状态2 大，比较图6、图7可见，随着目标误差的减小，逼近和泛化能力均有所提高。但目标误差也不宜太小，否则会大幅增加收敛时间，有时甚至无法达到。

对于隐含层数而言，多隐含层BP 网络具有更快的训练速度、更好的逼近能力和鲁棒性，但随着层数的增多，网络复杂度会大幅增加，在实际应用中需要可观的计算时间。通过增加隐含层节点数可以提高误差下降速度，但每一次循环中的计算量也随之增加，所需训练时间不一定会减少。

通过以上分析可见，神经网络训练参数的选取要兼顾逼近和泛化能力、精度和复杂度，同时还要考虑网络的鲁棒性和稳定性。本文在敏感性分析基础之上，确定了BPNN 以及RBFNN 的参数，并进行了训练。下面仍以BPNN 为例给出训练结果。图8 为磁化特性和转矩特性的BPNN 训练结果。所建立两个BP 神经网络均为二输入、单输出、双隐层结构，采用LM 学习算法。表3 给出了它们的主要结构及训练参数。

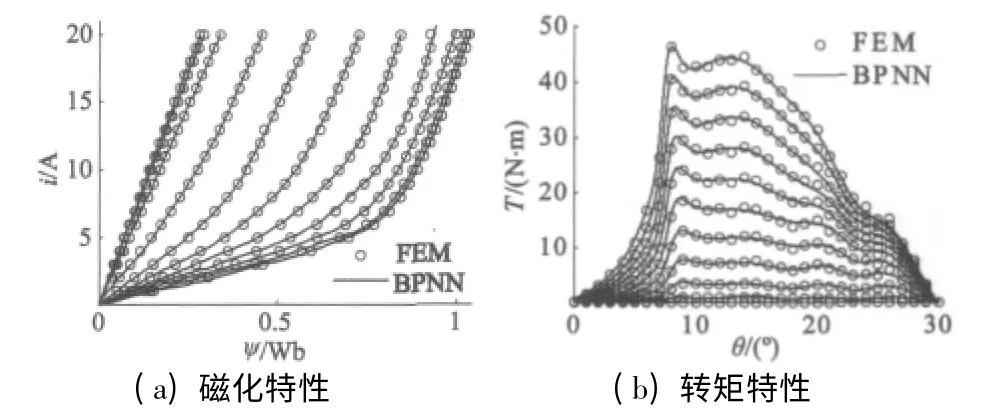
图8 所建立BPNN 的训练结果

表3 两个BP 神经网络结构及训练参数

4 SRM 动态仿真模型

根据式(1)～式(6)以及训练好的神经网络，可以很方便地搭建SRM 的动态仿真模型。本文将整个SRM 驱动系统仿真模型分为两个部分:功率变换器模块由电力系统工具箱(PSB)实现，而电机绕组模块、控制器模块等由自定义M 函数及Simulink 库中一些基本的模块搭建而成。该方法结合了基于电路仿真和微分方程仿真两种方法的优点，在不失精确性的同时还具有仿真速度快、修改容易、直观性强等特点。本文只对模型的核心－相绕组模块进行说明，其他部分的建模过程可参见作者的前期工作［11］。

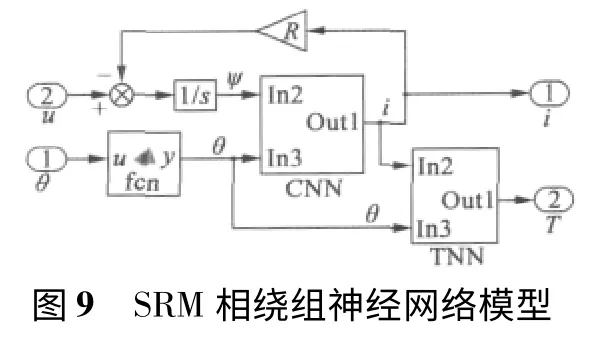
图9 给出了相绕组的模型，其中CNN 和TNN分别表示磁化特性和转矩特性非线性映射模块，可由训练好的BPNN 或RBFNN 实现。

5 仿真结果及分析

本文分别基于BP 神经网络和RBF 神经网络搭建了SRM 的动态仿真模型，为了验证所建模型的准确性，将不同工况下模型输出的电流、转矩曲线与FEM 的结果进行了详细对比。表4 给出了四种不同工况的控制模式及参数。

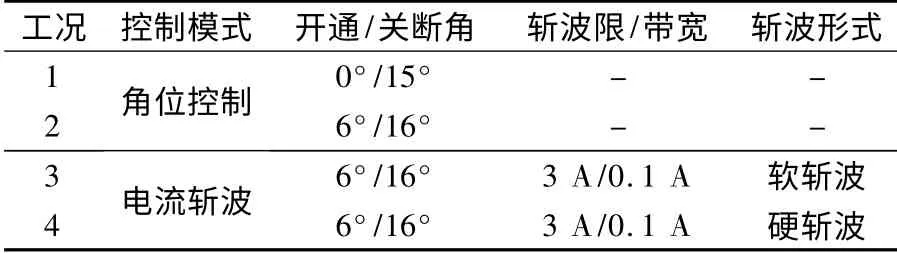
表4 两个BP 神经网络结构及训练参数

图10、图11 分别给出了上述四种工况下BPNN模型和RBFNN 模型仿真结果与FEM 的对比，其中实线为FEM仿真结果，虚线为相应动态模型的输出。

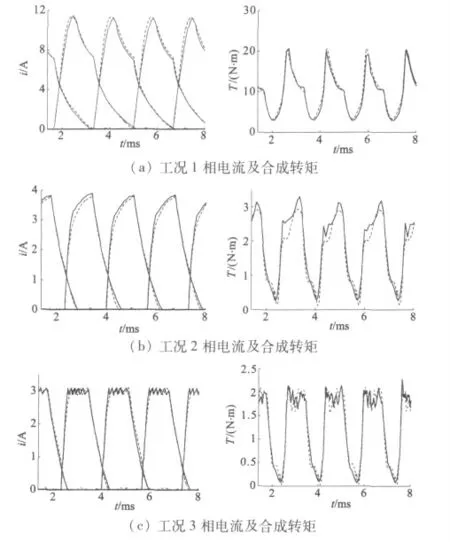
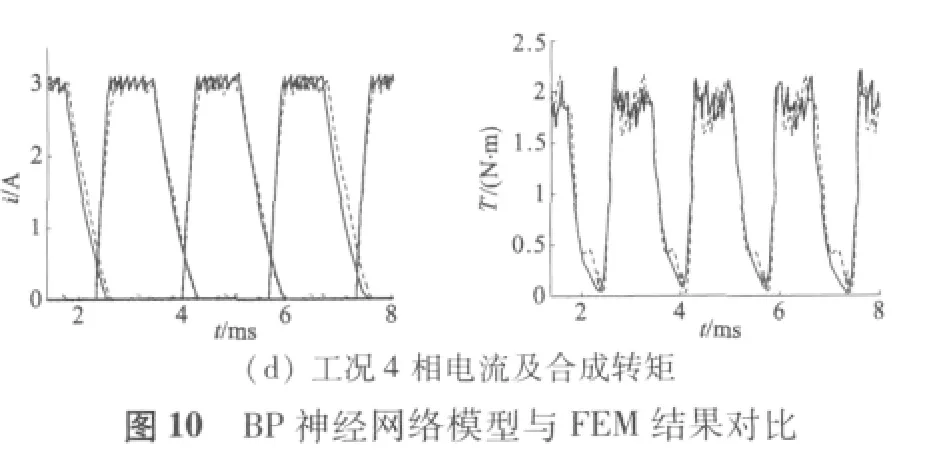
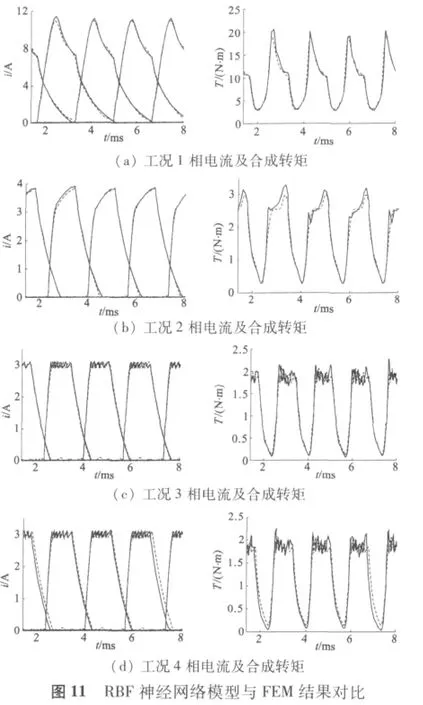
由图可见，两个模型均能准确反映不同工况下SRM 的动态特性，相电流及合成转矩曲线与FEA 分析结果具有很好的一致性，且RBFNN 的仿真精度总体要比BPNN 高。在训练过程中发现，BPNN 的构建较为复杂，训练参数确定工作量大，容易陷入局部极小点，且训练结果受权值初始值的影响很大。而RBFNN 则构建简单，网络结构和训练参数调整方便，训练时间短，结果稳定，不存在局部极小等问题，具有一定的性能优势。但RBFNN 的隐层神经元数远远高于BPNN，使其复杂度大大增加，结构庞大，从而运算量也有所增加。

6 结 语

本文将数值和映射建模法相结合，基于BP和RBF 神经网络技术，建立了一个4 相8 /6 极SRM 的动态仿真模型。通过对神经网络结构及训练参数的敏感性分析，优化了取值，提高了逼近及泛化能力。仿真及对比分析结果表明，两个仿真模型均具有较高的仿真精度，且RBF 神经网络的整体性能要优于BP 神经网络。然而，随着各种改进方法的提出和应用，相信BP 神经网络的性能会有很大的提高。本文的研究结果可直接用于对SRM 驱动系统控制参数的自主优化，也可为后续电机尺寸到性能的直接映射和迭代优化打下基础。

［1］ Vijayakumar K，Karthikeyan R，Paramasivam S，et al．Switched reluctance motor nodelling，design，simulation，and analysis:a comprehensive review ［J］．IEEE Transactions on Magnetics，2008，44(12):4605－4617．

［2］ 宋受俊．Detailed design of a 30 kw switched reluctance sarter/generator system used in more/all electric aircraft ［M］．德国:Shaker出版社，2009．

［3］ Zhu Z Q，Chan C C．Electrical machine topologies and technologies for electric，hybrid，and fuel cell vehicles［C］/ /IEEE Vehicle Power and Propulsion Conference．2008:1－6．

［4］ Cardenas R，Pena R，Perez M，et al．Control of a switched reluctance generator for variable－speed wind energy applications ［J］．IEEE Transactions on Energy Conversion，2005，20(4):781－791．

［5］ Lin D，Zhou P，Stanton S，et al．An analytical circuit model of switched reluctance motors ［J］．IEEE Transactions on Magnetics，2009，45(12):5368－5375．

［6］ Ding W，Liang D．A fast analytical model for an integrated switched reluctance starter/generator ［J］．IEEE Transactions on Energy Conversion，2010，25(4):948－956．

［7］ Ghousia S F，Kar N．Performance analysis of an 8 /6 switched reluctance machine using finite－eement method［C］/ /IEEE Power Engineering Society General Meeting．2007:1－7．

［8］ Sun H，Gao J，Dong Y，et al．Analysis of temperature field in switched reluctance motor based on finite－element［C］/ /International Conference on Electrical Machines and Systems．2008:597－601．

［9］ Cai Y，Gao C．Nonlinear modeling of switched reluctance motor based on BP neural network ［C］/ /Third International Conference on Natural Computation．2007:232－236．

［10］ Cheng Y，Lin H．Modeling of switched reluctance motors based on optimized BP neural networks with parallel chaotic search ［C］/ /2nd International Asia Conference on Informatics in Control，Automation and Robotics．2010:153－156．

［11］ 宋受俊，刘卫国．开关磁阻发电系统非线性建模及故障仿真研究［J］．系统仿真学报，2008，20(6):1434－1440．