超声波电动机特征模型的辨识建模
尤冬梅,史敬灼
(河南科技大学,河南洛阳471003)
0 引 言
超声波电动机的数学模型是其控制系统分析、设计与性能评估的重要基础。为提高超声波电动机运动控制装置的性能,研究更为合理的控制策略,必须得到适合于控制应用的超声波电动机数学模型。
由于超声波电动机运行机理的复杂性,基于实验数据的辨识方法成为建立超声波电动机控制模型的主要方法[1]。但通常认为,辨识模型只是对超声波电动机在最小二乘意义下的近似,难以表述其全貌。即,辨识模型能够描述超声波电动机的主要运行特征,但不是对超声波电动机的完整准确描述。这就使得基于辨识模型的超声波电动机控制器设计必须适应于这一模型偏差。
吴宏鑫院士提出的特征模型[2]是一种基于实验数据的模型,可将其归入辨识模型的范畴。但不同的是,已有理论证明,实时修正的低阶(二阶或三阶)特征模型是对高阶实际对象的准确描述。基于特征模型,有可能得到较为简单的控制器结构。
本文给出了超声波电动机特征模型的辨识建模方法,提出了三种确定辨识算法参数初值的确定方法,通过误差比较确定了适合于超声波电动机建模与控制的参数初值和在线递推算法,计算结果表明了所建特征模型的有效性。
1 超声波电动机的特征模型
广义地说,特征模型是一种辨识模型形式。因为机电能量转换及摩擦传递过程的复杂性、时变性与分散性,难于通过理论分析得到能够精确描述超声波电动机动态运行特征的数学建模。因此,目前在超声波电动机控制装置的研究过程中,辨识建模方法应用越来越广。
辨识建模方法以实验数据为主要依据。建模的目的是获取一个能够逼近实验数据所描述的动态特征的模型。对于时变对象,可以采用在线递推的辨识算法,来获取系数变化的辨识模型。辨识理论指出,无论是通过辨识得到的固定系数模型还是时变系数模型,都只是对实际对象的一种近似。理想情况下,这种近似是在误差平方和意义上的最佳逼近。由于辨识模型的“近似”特征,基于该模型的控制器离线设计和在线自适应,也就都有了“近似”的性质。
那么,采用适当的辨识方法和适当的模型形式,是否有可能得到更好的对象模型?特征模型理论[2]表明,时变的低阶模型与高阶系统等价。即通过设计适当的低阶模型形式,并采用适当的在线辨识算法获取时变的模型系数,所得的变系数低阶模型与高阶系统等价。
对于线性定常系统而言,其特征模型是由特征变量和部分特征参量通过线性组合所构成的慢时变差分方程。其中,特征变量是实际系统的量测输入和量测输出,特征参量指的是在特征模型中能够反映这些特征变量之间关系的参量,如阶次、时变的模型系数等。该模型的参数是时变的,而不是固定的。特征模型的建立过程就是一个在线、实时的递推辨识过程。建立系统的特征模型,就是建立一个包含在线辨识过程的低阶时变模型,每一时刻的特征模型都可以完全表述该时刻的实际系统;即每一时刻的特征模型均与实际系统等价。
下面,尝试建立超声波电动机的特征模型。
2 超声波电动机的固定参数模型
为建立超声波电动机的特征模型,首先需要建立其固定参数模型。原因有三,一是为特征模型结构的选择做准备,确定具有较小误差平方和的模型结构;二是对比辨识方法,确定合适的辨识算法来辨识特征模型的参数初值;三是用来与所建特征模型进行模型误差对比。
2.1 实验数据的筛选
辨识建模方法以实测的输入、输出数据为基础。自行设计的转速控制实验系统[3]结构如图1 所示,所用两相行波超声波电动机为Shinsei USR60 型,关于该系统结构的描述参见文献[3]。改变图1 中的电机转速给定值Nref及转速控制器控制方式,测取不同转速、不同控制动态过程情况下的阶跃响应过程数据用于建模。选择其中10 组数据作为建模数据,这些数据涵盖了实验电机转速的可调范围0~120 r/min。除此之外,另选5 组转速给定值分别为120 r/min、100 r/min、90 r/min、80 r/min、30 r/min的实验数据作为验证数据,用来验证所建模型的有效性,也有助于选择辨识算法。

图1 转速控制实验系统结构
应指出的是,为了保证数据测量的完整性,所测阶跃响应数据中包含较多的转速稳态运行数据。从原理上讲,辨识建模的过程是一个以拟合建模数据为目的的优化过程,过多的稳态运行数据可能使辨识结果背离所期望的超声波电动机动态模型。所以在辨识之前,剔除了实测数据中过多的稳态数据。
本文所述模型以电机驱动电压的频率u(k)为输入,输出y(k)为电机转速。
2.2 辨识方法的选择与对比
一般地,辨识模型可表述:

A(z-1)和B(z-1)的阶次na、nb,及延迟阶次d,由基于实验数据的最小二乘模型结构辨识确定。选取转速给定值为90 r/min 的实验数据进行模型结构的辨识,计算结果表明当na= 3、nb= 2、d = 0 时,所得模型损失函数和最终预报误差最小。下文按此阶次进行超声波电动机模型辨识。
为了确定适合于超声波电动机的辨识方法,分别采用最小二乘一次完成算法(LS)、递推最小二乘法(RLS)、递推增广最小二乘法(RELS)、递推极大似然法(RML)进行模型参数辨识,通过对比每种方法的误差平方和来确定辨识方法。计算结果如表1 所示。

表1 不同辨识算法建模误差对比
从建模数据的误差平方和来看,LS 和RML 均取得了相对较小的值,分别为229.134 5和229.393 0。从验证数据来看,LS 的验证结果也与RML 相近,由于RML 相对复杂,故选用LS 来辨识特征模型参数初值。用LS 所建模型,验证数据的模型输出与实测数据对比如图2 所示,可见模型输出与实测值基本一致,最大误差绝对值为6.577 r/min。
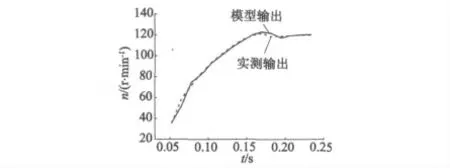
图2 模型输出与实测数据对比(Nref = 120 r/min)
3 特征模型的建立
根据上述建立固定参数模型的过程,通过比较不同模型结构时的误差平方和,特征模型的结构可选为三阶,即na= 3、nb= 2。通过对比辨识算法的辨识效果,可选择最小二乘一次完成算法来辨识特征模型参数初值。于是,超声波电动机的特征模型可写成:

式中:y(k-n)、u(k-n)分别为前n 时刻的转速和频率控制字;a1(k)、a2(k)、a3(k)、b0(k)、b1(k)、b2(k)为时变的特征模型参数。
确定模型结构后,建立特征模型还需确定辨识算法初值和在线递推算法。
3.1 辨识算法的参数初值
为使辨识算法可在线计算,需给定递推算法中矩阵θ(k)、P(k)的初值θ(0)、P(0)。考虑超声波电动机运行特性,提出下列三种矩阵θ(0)确定方法(下文简称这三种初值确定方法为方法1、方法2、方法3):
(1)由上述分析,通过比较几种辨识方法所得的固定参数模型的误差平方和,用误差平方和最小的那个辨识方法所得模型参数作为参数初值。
(2)由于电机系统由零转速开始运转,θ 初值主要对控制的起始阶段起作用,而这一起始阶段必定是从零转速开始的低速运行区域。所以,可将θ初值设置为低速情况下的离线辨识所得参数。
(3)对于不同的给定转速,分别用最小二乘一次完成算法作三阶的模型辨识,每个给定转速对应一组模型参数,该参数分别作为各给定转速辨识参数的初值,若有多组相同给定转速的数据,其初始参数值θ(0)为该多组观测数据组合起来最终辨识的结果。
状态估计误差的协方差阵P 与模型参数修正作用大小直接相关,协方差越大,说明估计值与真实值相差越大,增益向量也会越大,所产生的模型参数修正作用也越大。本文在辨识计算过程中,取P 的最初值为足够大的正值,并将辨识计算结束时的P值取做下次辨识计算过程的初值,以增加辨识算法在少量数据情况下的收敛能力。
3.2 辨识算法的确定
在确定了初始参数的取值后,就要确定特征模型的在线递推算法,为了选择更为合适的在线递推算法,分别采用RLS、RELS、RML 进行递推计算,根据特征模型具有参数时变的特点,计算程序在递推过程中的误差平方和,即每一次采样就计算一次误差平方和。通过对比每种方法的误差平方和来选择合适的辨识方法。计算结果如表2 所示。

表2 各辨识方法不同确定参数初值方法的误差平方和对比
表2 中,对于RLS、RELS、RML 这三种辨识方法,不论从建模数据还是验证数据来看,第三种参数初值确定方法的误差平方和都小于前两种;再对比第三种参数初值确定方法,RELS 和RML 的误差平方和都小于RLS 的误差平方和,其中RML 略大于RELS。综合考虑,特征模型的建立选择增广最小二乘辨识方法(RELS)作为在线递推算法,同时选择第三种参数初值的确定方法。
基于超声波电动机的特征模型式(2),选用第三种参数初值的确定方法,通过增广最小二乘辨识算法的循环递推计算,验证数据的模型输出与实测数据对比图如图3 所示,分别选取Nref= 120 r/min和Nref= 30 r/min 的验证数据进行对比。与图2 相比,图3(a)中最大误差绝对值仅为2.62 r/min,模型误差有明显改善;图3 (b)中最大误差绝对值0. 56 r/min,误差也较小,模型计算输出逼近实测数据输出。
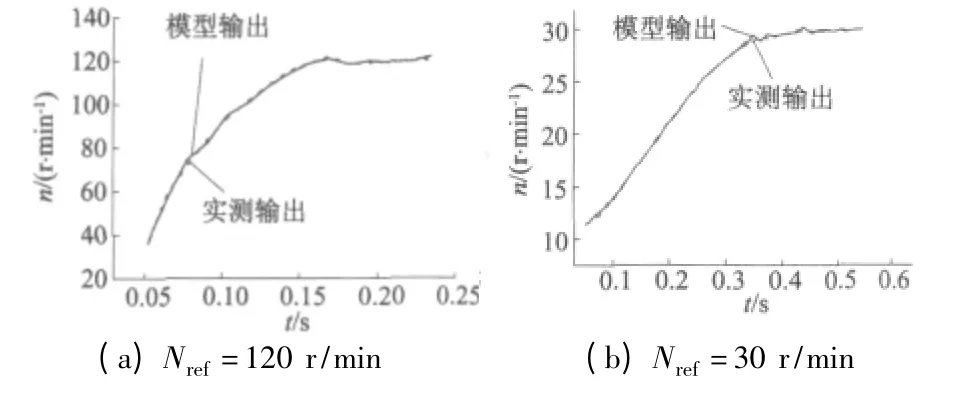
图3 模型输出与实测数据对比
图4 为数据在辨识过程中的误差变化情况。从图中可以看出,误差在零值上下浮动,并且偏离0 值不远,即转速误差不大,所建特征模型的模型输出与实测数据相当接近,特征建模能够准确逼近对象特性。

图4 辨识过程中的误差变化
3.3 固定参数模型与特征模型对比
由固定参数模型与特征模型的建立过程可得表3。

表3 不同辨识算法固定参数模型与特征模型误差平方和对比
通过对比固定参数模型与特征模型建模、验证数据的误差平方和可知,分别从建模数据和验证数据来看,对于这三种辨识算法的计算结果,无论哪一种算法均是特征模型的误差平方和小于固定参数模型的误差平方和。
另外,由表4 的误差对比可知,转速为120 r/min 时,与固定参数模型输出相比特征模型输出误差明显较小;转速为30 r/min 时,特征模型的误差也不大。可见,特征模型输出更逼近实测数据输出,能够对实际系统更完全的表述。

表4 验证数据的模型输出误差对比
4 结 语
数据对比表明,与通常的辨识模型相比,特征模型能够更好地表述超声波电动机驱动控制系统的内在非线性特征。本文的工作为超声波电动机的控制建模提供了一种可行方法,也为进一步运动控制策略设计提供了必要基础。
本文所述建模方法也可用于传统电磁电机的建模。
[1] 张新良,谭永红.行波型超声电机基于输入电压变化的参数模型辨识[J].系统仿真学报,2008,20(13):3492-3495.
[2] 吴宏鑫,胡军,谢永春.基于特征模型的智能自适应控制[M].北京:中国科学技术出版社,2008.
[3] 吕琳,史敬灼.基于蚁群优化的超声波电动机系统动态模糊辨识建模[J].微特电机,2011,39(10):58-60.

