无刷双馈电机新型控制策略综述
高保龙,韩 力,杨 硕,潘红广
(1.重庆大学,重庆400044;2.西电济南济变志亨电力设备有限公司,济南250300)
0 引 言
无刷双馈电机(以下简称BDFM)于20 世纪初由Hunt 和Broadway 等学者在自级联绕线式异步电机的基础上提出[1-2]。BDFM 结构简单、坚固耐用,取消了电刷和滑环、运行可靠,转速与功率因数可灵活调节,可单馈或双馈运行,所需变频器容量小、系统成本低,因而在变频调速传动及变速恒频发电系统有着广阔的应用前景。
目前针对BDFM 控制策略研究较多的有标量控制、矢量控制及直接转矩控制[3-5]。但由于BDFM 为高阶、多变量、非线性及强耦合的系统,且在实际控制时存在外部干扰,故上述几种控制策略都存在不同程度的局限性[6]。
20 世纪80 年代以来,针对非线性系统控制策略的研究取得了令人瞩目的成就,国内外学者提出了自抗扰控制、无源性控制及滑模变结构控制等一系列新型控制策略[7-8],并将其应用到交流感应电机的控制中,取得了较好的控制效果[9-14]。由于BDFM 是一种特殊的交流感应电机,在起动或运行时具有感应电机的基本特性,故受感应电机新型控制策略的启发,人们对BDFM 的新型控制策略开展了卓有成效的研究,提出了BDFM 的自抗扰控制[15-17]、无 源 性 控 制[18-21]和 滑 模 变 结 构 控制[22-25]。但目前针对上述BDFM 新型控制策略的综述论文尚未见报道。
本文在介绍BDFM 系统结构与数学模型的基础上,较全面地分析了当前BDFM 新型控制策略的研究现状及局限性,展望了其发展趋势,为BDFM控制策略的深入研究提供一些新思路。
1 BDFM 的系统结构与数学模型
BDFM 系统的结构如图1 所示,其定子包括两套三相绕组,一套为极对数为pp的功率绕组,另一套为极对数为pc的控制绕组。功率绕组直接与工频电网相接,提供电机与电网之间主要的能量转换通道;控制绕组通过变频器接电网,通过改变变频器的输出电压与频率,来控制电机运行。定子功率绕组与控制绕组分别通以三相对称电流,通过转子的磁场调制作用来实现机电能量的转换。转子结构不同于普通的感应电机,分为笼型、磁阻型及绕线型等型式,无需电刷和滑环。BDFM 兼有异步电机和同步电机的特性,可自起动和异步运行,也可同步运行,并可实现低于和高于同步转速的双馈运行。

图1 无刷双馈电机系统结构示意图
为了实现对BDFM 的控制,需要首先建立其转子速dq 轴旋转坐标系下的数学模型。其电压方程[6,15,18-23,25-26]:
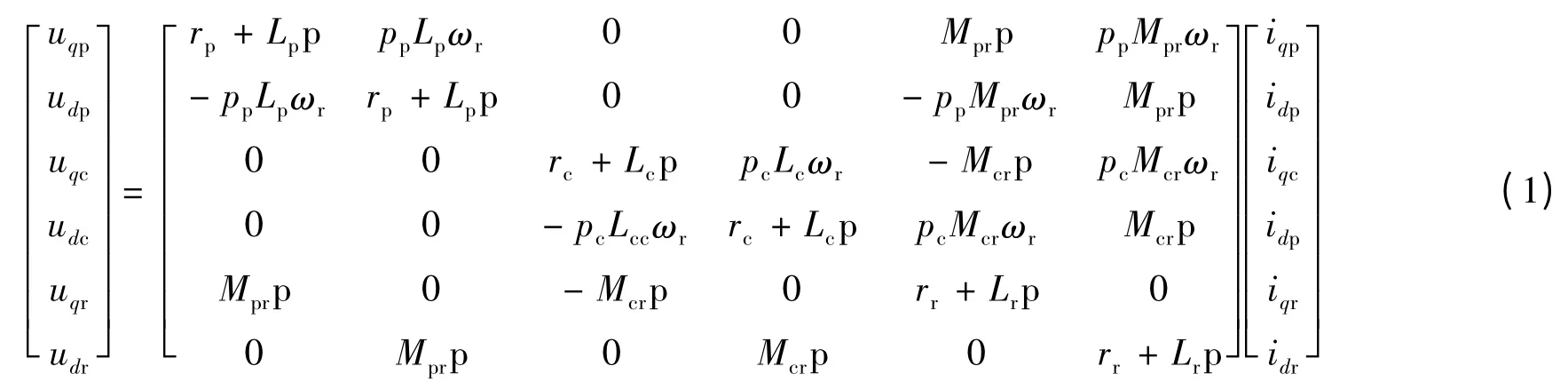
式中:udp、uqp、idp、iqp分别为定子功率绕组电压、电流的d、q 轴分量;udc、uqc、idc、iqc分别为定子控制绕组电压、电流的d、q 轴分量;udr、uqr、idr、iqr分别为转子绕组电压、电流的d、q 轴分量;Lp、Lc、Lr分别为定子功率绕组、定子控制绕组和转子绕组的自感;rp、rc、rr分别为定子功率绕组、定子控制绕组和转子绕组的电阻;Mpr、Mcr分别为定子功率绕组、定子控制绕组与转子绕组之间的互感;pp、pc分别为定子功率绕组和定子控制绕组的极对数;ωr为转子机械角速度;p 为微分算子。
BDFM 的电磁转矩[6,18-21,23,25-26]:

式中:Tep和Tec分别为定子功率绕组子系统和定子控制绕组子系统的电磁转矩。
BDFM 的机械运动方程[6,18-21,25]:
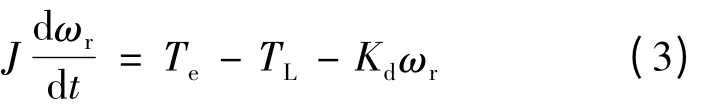
式中:J、Kd、TL分别为转子的转动惯量、阻尼系数和负载转矩。
这样,由式(1)~式(3)构成了BDFM 在转子速dq 轴旋转坐标系下的数学模型。
2 BDFM 的新型控制策略
BDFM 系统具有高阶、多变量、非线性、强耦合等特点。在式(1)~式(3)数学模型的基础上,经过进一步推导,可以得出所需的、适用于BDFM 新型控制策略的数学模型,进而实现BDFM 的自抗扰控制、无源性控制、滑模变结构控制等。下面具体介绍上述三种BDFM 新型控制策略。
2.1 自抗扰控制
自抗扰控制技术的核心是把系统的未建模动态和未知外扰作用归结为对系统的“总扰动”而进行评估并给予补偿。采用的方法是充分运用特殊的“非线性”效应,构造自抗扰控制器(以下简称ADRC)。ADRC 由跟踪-微分器(以下简称TD)、扩张观测器(以下简称ESO)和非线性状态误差反馈(以下简称NLSEF)三部分组成[11],如图2 所示。其工作原理:首先,用TD 来对系统输入信号v(t)进行快速无超调地跟踪,并对其给出广义各阶微分信号z11,z12,…,z1n;然后通过ESO 对系统的状态z21,z22,…,z2n和总扰动z2,n+1分别进行估计;将上述两种信号分别做差得到的误差信号e1,e2,…,en提供给NLSEF;最后,NLSEF 根据误差信号获得控制量来补偿扰动分量Δ(t),进而达到预期的控制目标。

图2 自抗扰控制器结构框图
根据以上原理,文献[15-16]先后对应用于风力发电系统中的BDFM 自抗扰功率解耦控制进行了研究。文献[15]首先根据式(1)~式(3)将BDFM 分为功率绕组子系统和控制绕组子系统,并分别建立了各自同步坐标系下的数学模型,进而得出了BDFM 的功率解耦数学模型。在此基础上,设计了TD、ESO、NLSEF 构成ADRC。仿真结果表明,该控制策略能较好地实现BDFM 的功率解耦控制。文献[16]则着眼整个风力发电机组的稳态运行情况,对BDFM 功率解耦控制进行了研究。仿真结果表明,此控制方法能根据电网的实际需求调节机组的无功功率输出,成功实现了有功功率与无功功率的解耦控制。文献[17]对电流型变频器供电的BDFM 转矩、转速的自抗扰控制进行了研究,通过仿真验证了该方法的有效性,实现了转速环和磁链环的准确解耦。
由于ADRC 控制策略具有较好的解耦控制效果,能有效改善电机控制系统的动、静态性能,且鲁棒性强,因此在双馈风力发电系统及电机调速系统的应用也受到关注[13-14]。考虑到实际应用情况,ADRC 适合于阶数较低(如小于3)的被控对象,当被控对象的阶数大于3 时,得到一组满意的非线性函数及相应的参数比较困难;同时计算量大,实时性变差,导致控制周期变长,影响电机的控制性能。
基于ADRC 的BDFM 控制策略研究处于起步阶段,其理论分析和仿真研究尚不深入,尤其在控制器参数整定及发电运行时的并网控制方面需进一步研究。
2.2 无源性控制
无源性控制(以下简称PBC)方法最早应用于机器人控制。20 世纪90 年代末,墨西哥学者Ortega等将PBC 概念引入到电机和电力电子装置的控制中[27]。该方法着眼于系统的能量特性,首先配置系统能量耗散特性方程中的无功分量,然后设计相应的控制器迫使系统总能量跟踪期望的能量函数,进而使系统的状态变量渐进收敛至设定值,最终达到预期的控制目标。

图3 BDFM 的无源性控制系统框图
文献[18-19]对BDFM 的无源性控制进行了研究。应用PBC 理论,首先建立了BDFM 的欧拉-拉格朗日方程,并将其分解为电气和机械两个无源子系统的反馈互联,以此说明在设计控制器时只需考虑电气子系统,从而简化了控制算法。设计了BDFM 的转矩和转速控制器,其无源性控制系统如图3 所示。当得到转速、磁链给定值为ωr*、Ψ*时,电流观测器和转速观测器分别得到电流、转速测量值为iqc、idc和ωs,控制器经过对给定值和测量值的运算生成控制绕组dq 轴旋转坐标系下的控制量udc、uqc、ωr,将其进行坐标变换后,生成静止坐标系下的控制量ua、ub、uc,对BDFM 进行控制。仿真结果表明,无源性控制具有较好的动态性能。为了提高系统的鲁棒性,文献[20]在无源性控制的基础上,考虑BDFM 功率绕组及控制绕组电阻在运行中可能发生变化,设计了自适应控制器,并通过仿真验证了该方法的正确性和有效性。基于PBC 方法,文献[21]提出了一种新型转矩和转速控制结构,并设计了相应的非线性控制器。仿真结果显示,新型控制器可以准确实现BDFM 转矩、转速的跟踪控制,具有控制结构简单、动态响应性能优良、鲁棒性好的优点。而且PBC 方法比矢量控制方法减少了计算量;比直接转矩控制方法减小了转矩脉动。
由于PBC 基于能量的观点,是本质的非线性控制,能够全局稳定且无奇异点、鲁棒性强,因此PBC适用范围广泛,例如电机低速或起动、系统参数发生变化及受到外来扰动等情况[11]。但目前针对无源性控制在交流感应电机方面应用的研究普遍不够深入,还有很多问题有待于进一步研究,比如其能否跟踪任意曲线,特别是未知的时变曲线;其控制律比较复杂,如何用实验来验证理论结果,进而如何实现工程应用等[10,28]。
尽管如此,目前针对感应电机控制策略的研究文献表明,在诸多控制策略中无源性控制性能是最好的[9-11,28]。鉴于BDFM 本身就是一种特殊的交流感应电机,且PBC 策略对机电系统具有广泛的适用性,因此对BDFM 的无源性控制策略的研究将是一个非常有价值的研究方向,值得深入研究。
2.3 滑模变结构控制
滑模变结构控制是前苏联学者Utkin 等人提出的一种变结构控制策略[29]。其一般定义如下,考虑一般情况下非线性系统x.= f(x,u,t),x ∈Rn,u ∈Rm,分别是系统的状态和控制向量,首先确定一切换函数s(x,t),s∈Rm,然后求解控制函数:

式中:ui+(x,t)≠ui-(x,t),使得系统满足三个条件,即滑动模态存在、满足可达性条件和保证滑模运动的稳定性,此即为滑模变结构控制[8,24]。
文献[22]对基于滑模变结构控制的BDFM 有功功率和无功功率解耦控制进行了研究。首先根据BDFM 电压源dq 轴数学模型得到状态方程,然后根据有功功率、无功功率给定值选取滑模面,利用Lyapunov 函数求得相应的有功功率、无功功率滑模控制律,进而对BDFM进行滑模变结构控制,其控制系统如图4 所示。仿真结果表明,该方法能够成功实现风力发电中BDFM 有功功率与无功功率的解耦控制,同时实现风能的最大功率捕获,证明该控制器具有较强的鲁棒性。文献[23]针对BDFM 直接转矩控制系统磁链和转矩脉动大的问题,引入滑模变结构控制策略。以转矩和磁链两个滑模控制器来代替传统直接转矩控制中的两个滞环控制器,进而应用指数趋近率方法设计滑模控制器并由Lyapunov 方法求得相应的滑模变结构控制律。仿真结果表明,该控制策略能有效减小转矩脉动,改善定子磁链和电流波形,同时仍可保持直接转矩控制固有的转矩快速响应的优点,提高系统的稳定性和鲁棒性。

图4 BDFM 的滑模变结构控制框图
针对滑模变结构控制BDFM 调速系统的抖振问题,文献[24]提出多输入高阶滑模控制方法实现了BDFM 功率解耦控制,文献[25]则提出了基于自适应模糊方法的滑模变结构控制策略。仿真结果表明,上述控制方法都能有效消除滑模变结构控制的抖振,从而表明该方法的正确性及有效性。
滑模变结构控制具有不依赖系统结构和参数、整个设计过程思路清晰、易于实现等特点,在风力发电系统中已有成功应用[30]。但是目前针对BDFM滑模变结构控制的理论分析和仿真研究还不够深入,且相关实验验证尚未见报道。此外,滑模变结构控制策略本身也有控制律中存在不利抖振、匹配条件局限等缺点[8]。因此,对BDFM 的滑模变结构控制开展更深入的理论分析、仿真研究和实验验证,以及如何更好地弥补上述缺点,是值得进一步深入研究的问题。
3 结 语
本文简要介绍了BDFM 的系统结构与数学模型,阐述了BDFM 的自抗扰控制、无源性控制和滑模变结构控制等三种新型控制策略的基本概念。在此基础上,较全面地分析了上述BDFM 新型控制策略的研究现状、优势及应用场合。
由于BDFM 新型控制策略的研究还处于起步阶段,上述三种新型控制策略还存在基础理论不够完善、仿真研究不够深入及实验验证尚未进行等方面问题。因此,为了寻求更好的控制策略以进一步提高BDFM 的控制性能,首先需要继续对上述新型控制策略作深入理论分析,完善基础理论,拓宽适用性;其次,可以寻求两种甚至多种控制策略相结合,突破单个控制策略本身的缺点及局限性,进而提高控制性能。最后,根据不同的应用场合,对控制策略进行相应的合理简化,缓解精确性、快速性与复杂性之间的矛盾。以此简化控制器的设计,进而对上述新型控制策略进行硬件实现和实验研究,以期最终通过实验数据来验证新型控制策略的可行性、正确性和有效性。
[1] Hunt L J.A new type of induction motor[J].Journal Institute of Electrical Engineer,1907,39:648-667.
[2] Brodway A,Burbidge R L.Self-cascade machine:a low-speed motor or high frequency brushless alternator[J].IEE Proceedings,1970,117(7):1277-1290.
[3] Wu Tao,Wang Xuefan.The scalar control research based on fuzzy PID of BDFM stand-alone power generation system[C]/ /2011 International Conference on Electric Information and Control Engineering (ICEICE),Wuhan,China,2011:2806-2809.
[4] Poza J,Oyarbide E,Sarasola I.Vector control design and experimental evaluation for the brushless doubly fed machine[J].IET Electric Power Applications,2009,3(4):247-256.
[5] Sarasola I,Poza J,Rodriguez M A,et al.Predictive direct torque control for brushless doubly fed machine with reduced torque ripple at constant switching frequency[C]/ / IEEE International Symposium on Industrial Electronics.2007:1074-1079.
[6] 刘航航,韩力.无刷双馈电机控制策略发展综述[J].微特电机,2010(6):69-73.
[7] Alleyne A.Nonlinear system:analysis,stability and control[J].IEEE Transactions on Automatic Control,2000,45(12):2438 -2439.
[8] 贺昱曜,闫茂德.非线性控制理论及应用[M].西安:西安电子科技大学出版社,2007:149-155,161-163,185-188.
[9] Mendes E,Tijerina-Araiza A.Experimental comparison between field oriented control and passivity based control of induction motors[C]/ /Proceedings of the IEEE International Symposium on Industrial Electronics Conference.1997:84-88.
[10] 李伟.感应电机的非线性控制研究[D].广州:华南理工大学,2002:3-5,106.
[11] 王久和.交流电动机的非线性控制[M].北京:电子工业出版社,2009:5-7,166-167.
[12] 纪志成,薛花,沈艳霞.感应电动机无源性控制方法研究[J].电工技术学报,2005,20(3):1-6.
[13] Zheng Qing.Reduced-order active disturbance rejection control for induction motors[C]/ /2011 IEEE International Conference on Control Applications (CCA).2011:1139-1144.
[14] Zhou Xuesong,Li Chao.Application of ADRC in variable-speed constant-frequency wind energy generation with doubly-fed induction generators[C]/ /Proceedings of the 29th Chinese Control Conference.2010:6061-6065.
[15] 张有松,杨俊华,林建华,等.无刷双馈风力发电机的自抗扰解耦控制[J].水电能源科学,2007,25(6):146-149.
[16] 张先勇,舒杰,吴捷.无刷双馈风力发电机组的自抗扰功率解耦控制[J].太阳能学报,2008,29(12):1477-1483.
[17] 刘重春.无刷双馈电机的自抗扰控制策略研究[J].江汉大学学报(自然科学版),2006,34(1):60-62.
[18] 吕慧子,杨俊华,杨金明,等.无刷双馈调速电机无源性分析及自适应控制[J].控制理论与应用,2009,6(12):1425 -1429.
[19] 侯祖锋.无刷双馈风力发电系统的无源性控制研究[D].广州:广东工业大学,2011:58-65.
[20] 吕慧子.无刷双馈电机控制方法研究[D].广州:广东工业大学,2009:52-68.
[21] 韩力,潘红广,刘航航,等.无刷双馈电机转矩和转速的无源性控制[J].电机与控制学报,2011,15(11):1-7.
[22] 张先勇,吴捷,杨俊华,等.无刷双馈风力发电机滑模功率解耦控制[J].太阳能学报,2007,28(1):68-73.
[23] 杨俊华,刘远涛,谢景凤,等.无刷双馈电机滑模变结构直接转矩控制[J].控制理论与应用,2011,28(9):1195-1201.
[24] Valenciaga F.Active and reactive power control of a brushless doubly fed reluctance machine using high order sliding modes[C]/ /Proceedings of the 18th International Conference on Electrical Machines.2008:1-6.
[25] Shao Zongkai,Zhan Yuedong.Adaptive fuzzy sliding mode control for brushless doubly fed machine[C]/ / ISCID’09 Second International Symposium on Computational Intelligence and Design.2009,2:73-77.
[26] Li R,Wallace A.Two-axis model development of cage-rotor brush-less double-fed machines[J].IEEE Transactions on Energy Conversion,1991,6(3):453-460.
[27] Romeo Ortega,Antonio Loriad.Passivity-based control of Euler-Lagrange systems [M].Berlin:Springer,1998:265-308.
[28] 马良河,姜建国.异步电动机的无源性控制:现状和发展[C]/ /中国电工技术学会电控系统与装置专业委员会第十一届学术年会论文集.西安,2002:1-4.
[29] Utkin V I.Variable structure system with sliding modes[J].IEEE Transactions on Automatic Control,1977,22(2):212-222.
[30] Valenciaga F,Evangelista C A.2-sliding active and reactive power control of a wind energy conversion system[J].IET Control Theory & Applications,2010,4(11):2479-2490.

