基于滑模控制的永磁同步电动机q 轴电流在线检测
钟义长,钟伦珑
(1.湖南工程学院,湖南湘潭411101;2.中国民航大学,天津300300)
0 引 言
永磁同步电动机具有结构紧凑、体积小、重量较轻以及运行可靠、效率高、可控性好且易维护等优点,被广泛用于各种工业生产上。由于交流伺服系统的工作环境具有复杂性与多样性,使得采用传统控制方法对电机高精度的控制上就显得有点力不从心,于是这就提出了一个问题,即如何设计出高性能高品质的永磁同步电动机控制器[1]。
为了提高电机的控制精度,解决参数变化与扰动等不定因素对电机运行的影响,学者们采用了诸如自适应控制技术[2]、神经网络技术与重复控制技术[3-4]等。在文献[5-6]中,设计者引入了滑模变结构控制技术(SMC),使得电机对参数变化与负载扰动具有自适应能力,从而提高了系统的性能。
本文对照传统的控制方法,先提出滑模观测器的设计,为了计算电机的转速与位置,以αβ 轴下电压、电流为状态变量,同时采用了等效反电势信号。其中考虑到抖振信号对估算值的影响,本文对反电势信号先是低通滤波器滤波后再进行动态补偿;在得到转速与位置的基础上,然后利用滑模控制,提出对电机q 轴电流进行线上实时测量,这就避免了电流检测元件所带来的检测误差,从而使得电机控制精度得以提高。同时说明了这些算法的可行性,在文中也利用Lyapunov 方法证明了这些算法是收敛的,并且最后通过仿真验证了设计的可行性与有效性。
1 滑模观测器设计
1.1 引出观测器
两相静止α、β 坐标系下,表贴式永磁同步电动机的数学模型可表示:

式中:Rs、Ls为定子电阻与电感;分别为α、β 轴定子电压、电流、反电势。反电势满足,有为转子电角速度,ψf为磁链。
依据电机的数学模型,不妨在这里设计滑模观测器模型:

将式(2)减去式(1),易求得观测误差方程:
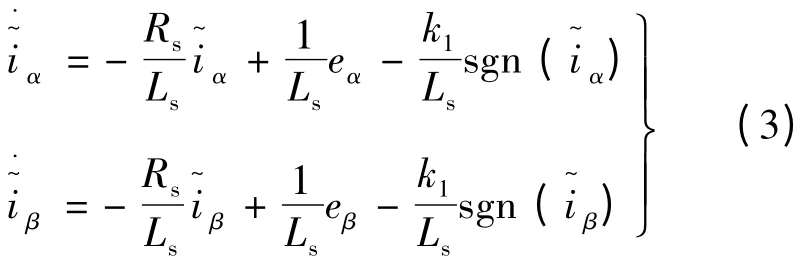

将式(4)这一滑模条件代入式(3)中,可得:

式中:定义z =(zα,zβ)T,显然为电流误差开关信号,其中含有反电势信息,也可表示:

式中:eα、eβ为反电势,Δ(t)为一扰动信号。采用低通滤波,就可得到反电势的估计值:

式中:ωc是滤波器截止频率。由此,转子位置角度可由式(8)计算:

由于低通滤波器易造成相位延迟,可以在式(8)所得相位角的基础上适当增加一补偿角,即:


对(10)式求导,电机转速估计值:

1.2 稳定性分析

这样,当滑模增益满足:k1>max(| eα|,| eβ|),滑模观测器稳定。
2 q 轴电流检测
传统电机的矢量控制,通常采用id= 0 的方法,这一方法其实是将转速误差经速度环后得电流控制环的输入信号i*q,然后由Δiq= i*q-iq来控制电机的绕组电压。这里对iq的获取则常用Clarke 变换和Park 反变换。检测元件的性能越好,所得到的iq值就越精确,所以对检测元件提出了高要求,而检测元件本身对电机参数的变化不是很敏感,其结果就会造成iq检测值的误差。本文在此提出仅由位置状态对iq电流来在线测量的一种滑模控制(SMC)方法。
由永磁同步电动机的运动方程[8]:
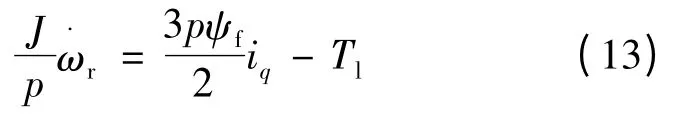
式中:p 为电机极对数,ψf为永磁体磁链,Tl为负载转矩,J 为转动惯量。对式(13),不妨设状态变量:

式中:ω*r、ωr分别为电机给定转速与实际转速。负载不变且只加入扰动时,对式(14)求导,则可得:
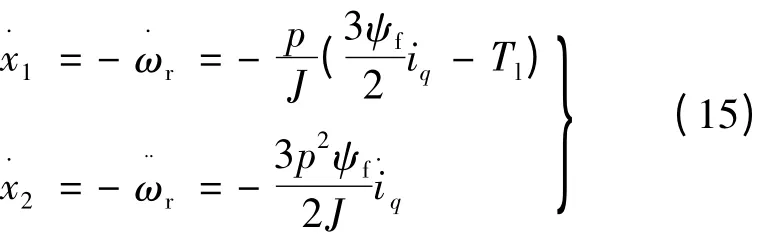


对全部状态变量进行反馈控制,令:
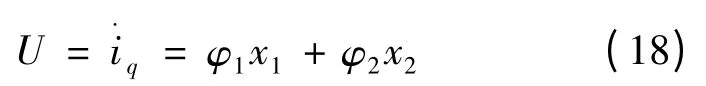

即可得:
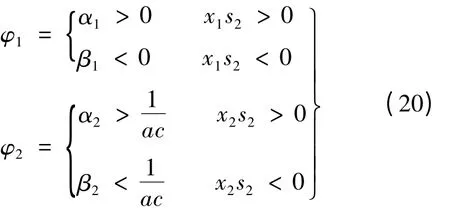
确定φ1、φ2之后,对式(18)积分,可得iq:
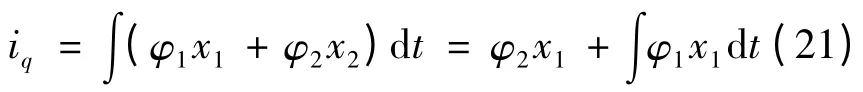
在式(21)中,x1包含ωr的信息,而由前面的推导,ωr可由式(11)得来,这样避开位置检测与电流检测中一些误差。
3 系统仿真分析
为验证本文方案,建立如图1 所示的控制系统原理图(令id= 0)。选择电机参数:p = 2,Rs= 3 Ω,Ls= 6 mH,ψf= 0.85 Wb,J = 0.001 J/(kg·m2)。PID 参数选择如下:速度环,kp= 5,ki= 2;q 轴电流控制,kp= 8,ki= 45;d 轴电流控制,kp= 1.5,ki= 10;滑模增益的选择为k1= 3 × 104。

图1 系统控制框图
图2 中,电机目标转速设为300 rad/s(其中在0.3 s 突加5 N·m 扰动,0.6 s 突卸该扰动)。本文控制下的系统,其估计转速可快速跟踪实际输出;且对突加与突缷负载仍能较准确地反映实际转速。图2(c)中q 轴电流的抖动比较小,说明了系统的鲁棒性较强。


图2 本文策略下电机转速及误差图形与q 轴电流波形
图3 是本文方案与纯双闭环PID 控制下响应比较。电机目标转速设为300 rad /s(其中在0.3 s 突加5 N·m 扰动,0.6 s 突卸该扰动)。很明显,PID控制的系统对突加、突缷负载情况下其转速波动较大,存在一个恢复时间;但本方案却能快速地恢复转速,对抑制超调、抗干扰上比PID 控制要优越。

图3 与PID 方案比较速度响应
为了能更好地说明本文方案,还与文献[10]一文所述方案进行了比较。电机目标转速设为300 rad /s(其中在0.3 s 突加5 N·m 扰动,0.6 s 突卸该扰动)。在同样的设定目标下,本文方案在速度的跟随性能与抗干扰上优于文献[10]方案。

图4 与文献[10]方案速度响应比较
4 结 语
本文针对永磁电机调速系统特点,在同步电动机数学模型的基础上,以静止坐标下电压、电流为变量,首先提出了一种自适应的滑模观测器的设计,同时对转子位置进行在线补偿,以弥补过滤时相位延时所造成的误差,并计算出电机转速。然后通过滑模变结构控制的方法,对q 轴电流进行了在线的检测,从而实现对电机的控制。仿真结果表明,系统能准确地对电机转速进行估计,同时在速度的跟随性能上又具有过渡时间短、超调小、抗干扰性与鲁棒性强的特点,说明了本文策略是有效性。
[1] Macro T,Francesco P,Zhang D Q.Real-time gain tuning of PI controllers for high-performance PMSM drives [J].IEEE Trans.on Industry Applications,2002,38(4):1018-1026.
[2] 刘志刚,李世华.基于永磁同步电机模型辨识与补偿的自抗扰控制器[J].中国电机工程学报,2008,28(24):118-123.
[3] Lin F J,Lin C H.A permanent magnet synchronous motor servo drive using self-constructing fuzzy neural network controller[J].IEEE Trans.On Energy Conversion,2003,19(1):66-72.
[4] Li X D,Chow T W S,Ho J K L,et al.Repetitive learning control of nonlinear continuous-time systems using quasi-sliding mode[J].IEEE Transactions on Control Systems Technology,2007,15(2):369-374.
[5] 吴春华,陈国呈.基于滑模观测器的无传感器永磁同步电机矢量控制系统[J].电工电能新技术,2006,25(2):1-3,51.
[6] 王家军,王江.基于逆变器死区的永磁同步电动机系统的变结构控制[J].控制理论与应用,2002,19(4):579-582.
[7] 鲁文其,胡育文,杜栩杨.永磁同步电机新型滑模观测器无传感器矢量控制调速系统[J].中国电机工程学报,2010,30(33):78-83.
[8] 黄佳佳,周波,李丹.滑模控制永磁同步电动机位置伺服系统抖振[J].电工技术学报,2009,24(11):41-47.
[9] 姚琼荟,黄继起,吴汉松.变结构控制系统[M].重庆:重庆大学出版社,1997.
[10] 任燕,刘卫国,皇甫宜耿.一种鲁棒滑模永磁同步电动机DTC控制[J].微特电机,2010,(2):56-59,66.

