电磁轨道炮二阶欠阻尼电路的模型构建与分析
王磊磊,刘 文 ,白象忠,吴榴红
(1.燕山大学 理学院,河北 秦皇岛 066004;2.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004;3.北方民族大学 信息与计算科学学院,宁夏 银川 750021)
电磁炮是利用电磁力加速驱动弹丸,使弹丸达到超高速的一种发射装置。如1978年澳大利亚的马歇尔利用同级发电机和等离子体电枢成功地将3 g重的弹丸加速到5.9 km/s。某研究所率先建造了国内首台电磁轨道发射试验装置,把0.34 g的弹丸加速到16.8 km/s的速度。相比之下常规火炮的发射速度仅能达到2 km/s,这一速度已接近物理极限。相反,电磁发射系统的推力比火药发射的推力大10倍,能把弹丸加速到每秒几公里至几十公里的高速度,使弹丸具有巨大的动能和极强的穿透力,从而大大提高了武器的射程和威力[1]。
文献[2]分析了轨道的热效应,因此,主要考虑移动载荷的电阻特性;文献[3-4]考虑了电流的趋肤效应,把弹丸看作是非线性变化的电阻和线性变化的电感;文献[5]分析了电磁轨道炮的模型。本文简单介绍了电磁炮的基本原理,建立了电磁炮的电路模型,根据此模型和电动力学原理,采用拉普拉斯变换求出了其二阶欠阻尼条件下的电路方程。
1 电磁轨道炮基本原理
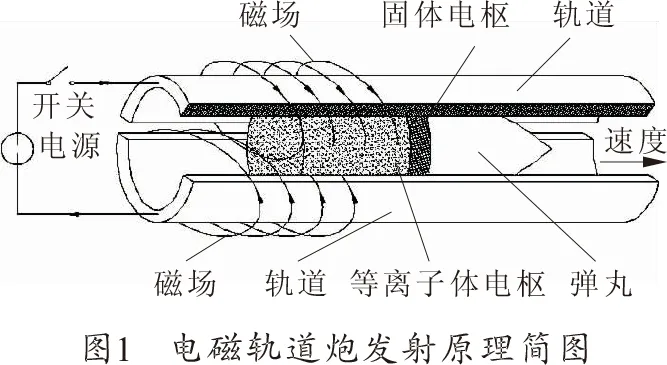
电磁炮按其结构不同,可分为轨道炮、线圈炮和重接炮三种。电磁轨道炮主要是由两条平行连接着大电流源的固定导轨和一个与导轨保持良好电接触、能够沿着导轨轴线方向滑动的电枢组成[6-7]。
图1给出了由电源、导轨、电枢和弹丸组成的电磁轨道炮发射装置示意图。当接通电源时,电流经过导轨、电枢后流回电源,构成闭合回路。流经导轨,电枢的电流在它们围成的区域内形成强磁场,该磁场与流经电枢的电流相互作用,产生强大的电磁力,该力将推动电枢和置于电枢前的弹丸沿着导轨作加速运动,直至将弹丸发射出去。
1.1 电枢所受电磁力分析
实际电磁轨道炮电枢运动过程要受到诸多因素的影响,如电枢与导轨内壁的摩擦力,空气阻力等,本文仅考虑电磁力对电枢的作用。假设在时刻t电枢所在的位置为x(t),此时整个系统的电感量为L(x),如果此时轨道中流过的电流为I(t),则整个系统的磁场能量为:
(1)
根据能量守恒原理,假设在极短的时间间隔Δt内,电枢受电磁力作用而移动了距离Δx,在此非常短的时间间隔内I(t)不随位置而变化,可以求得电枢所受的电磁力为[8]:
(2)
式中:电磁力F为电枢在轨道上受到的向前驱动力;W为系统储存的能量,主要为轨道分布电感的磁能;L′为电感增量,反映了单位长度导轨的电感;x为电枢运动的位移量。
1.2 电感梯度的分析
单位长度轨道的电感公式为[9]:
(3)
式中:d、w、h分别为导轨的厚度、间距和高度。
由式(3)可以看出电感梯度的变化与轨道的尺寸有密切的关系。
2 模型构建
电磁轨道炮的等效电路系统如图2所示,图中UC(t)为储能电容器上的电压;E(t)为电枢反电动势;R(t)为回路总电阻;L(x)为回路总电感;I(t)为放电回路电流。
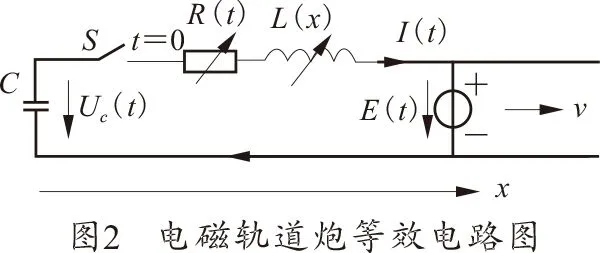
根据基尔霍夫第二定律,可得电磁轨道炮等效电路的回路方程[10]为:
(4)
由电路基本原理可知:
(5)
电磁力还可表示为:
F=B(t)I(t)w
(6)
式中:B(t)为磁感应强度;w为轨道间距。
联立式(2)和式(6)可得:
(7)
又因为反电动势可表达为[11]:
E(t)=vB(t)w
(8)
式中,v为电枢的运动速度。
联立式(5)、式(7)、式(8)可得:
(9)
将式(5)和式(9)代入式(4)整理可得:
(10)
计算该二阶电路的零输入相应。
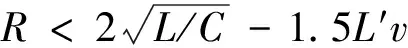
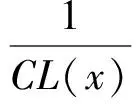
(11)
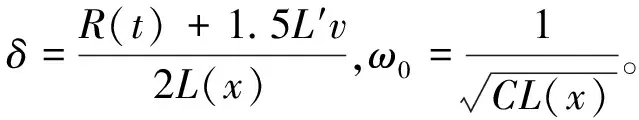
(12)
由上式用分部积分法得:
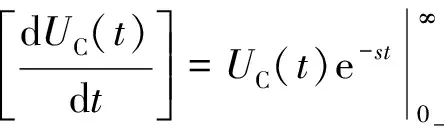
(13)
式中:UC(s)为电压UC(t)的象函数,且UC(t)e-st|t→∞=0。于是可得:
(14)
应用上式的结果可得:
(15)
将式(14)和式(15)代入式(11)整理可得:
(16)
对式(16)求拉普拉斯反变换过程如下,令:
可知式(16)为真分式。因D(s)是s的二次多项式,故可分解因式如下:
D(s)=(s-J1)(s-J2)
(17)
由于D(s)无重根,故J1≠J2,式(16)写成部分分式的形式为:
(18)
式中:l1和l2为待定常数,称为UC(s)在各极点处的留数。为确定两极点的留数,可将式(18)两边乘以因子(s-Jk),k=1,2。这样式(18)的右边出现仅留下包含系数lk的一项,再令s=Jk,代入整理可得式(16)的原函数为:
(19)
对于放电回路电流I(t),由式(5)可得:
(20)
对于电枢反电动势E(t),由式(9)可得:
E(t)=-l1CL′vJ1eJ1t-l2CL′vJ2eJ2t
(21)
因此,由式(19)、(20)和(21)可以对电磁炮的电路方程进行理论计算。本文通过对电感梯度的变换来分析说明储能电容器上的电压、放电回路电流和电枢反电动势之间的关系。
3 数值分析
由于电磁轨道炮尺寸的差异,其电感梯度也有所不同。储能电容器上的电压,放电回路电流,电枢反电动势可能会对轨道的电路产生影响,因此,有必要对其作比较分析。本文选取的相关参数如下:初始电压U0=10 kV,电容C=0.06 F,回路电感L=5×10-7H,回路电阻R=10-4Ω,出口速度v=3×103m/s(电磁炮目前努力达到的出口速度)。
图3给出了不同电感梯度对电压的影响。可以看出随着时间的变化,电压起初波动较大,随着电枢运动,时间变长,电压逐渐趋向于零。在所给的条件下,当L′=0.451 μH/m的电路在t=0.2 ms时的电压为U=5 394.930 2 V;而当L′=0.754 μH/m的电路在t=0.2 ms时的电压为U=6 019.809 4 V,前者比后者电压减少了11.58%。
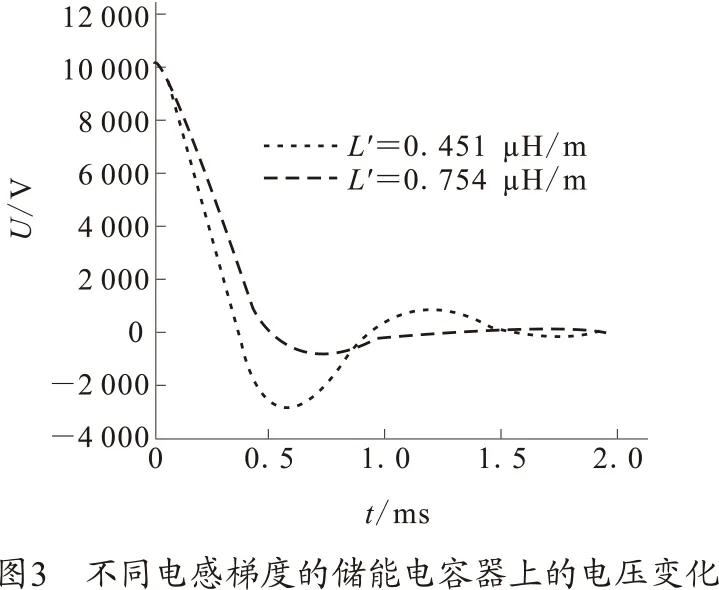
图4给出了电感梯度对放电回路电流的影响。可以看出随着时间的变化,电流先是迅速升高,达到电流峰值后,由于受到回路电阻的影响迅速减小,并逐渐趋向于零。在所给的计算条件下,当L′=0.451 μH/m的电路在t=0.22 ms时电流峰值达到I=2.157 5×106A;而当L′=0.754 μH/m的电路在t=0.2 ms时的电流峰值为I=1.720 5×106A,前者比后者时间增加了10%,电流峰值增加了25.4%。
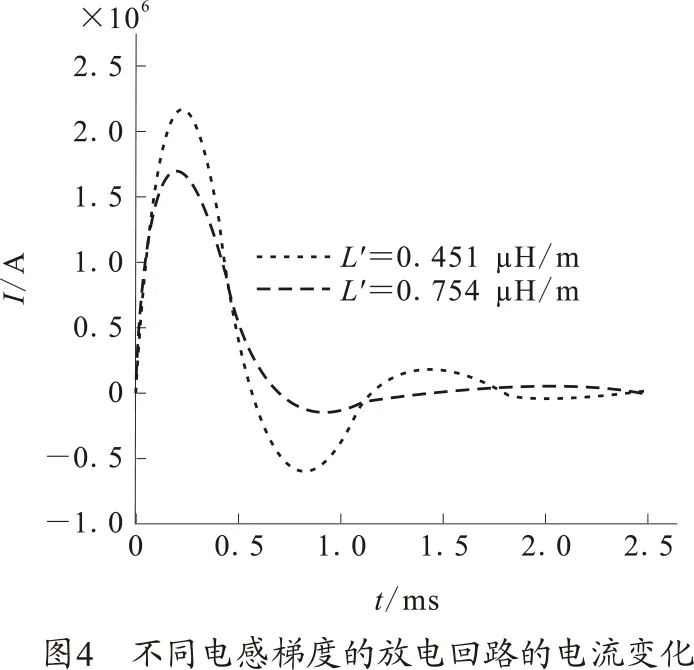
图5给出了电感梯度对电枢反电动势的影响。可以看出随着时间的变化,电枢反电动势先是升高,达到峰值后开始下降,最终趋向于零。在所给的条件下,当L′=0.451 μH/m的电路在t=0.22 ms时电枢反电动势的峰值为E=1 459.541 1 V;而当L′=0.754 μH/m的电路在t=0.2 ms时电枢反电动势的峰值达到E=1 945.886 3 V,前者比后者时间增加了10%,反电动势峰值减小了33.32%。
4 结 论
利用MATLAB软件分析了不同电感梯度对储能电容器上的电压、放电回路电流和电枢反电动势的影响,分析结果表明:电感梯度越大,电压波动越小,电流波动也越小,反电动势则越大。随着时间的变化,它们的波动频率先是比较显著,继而逐渐趋向于零。这种变化符合电路系统的规律,有助于对电磁炮电路的进一步研究和实验。
参考文献(References)
[1] 刘文, 李敏, 白象忠, 等. 电磁炮发射轨道受指数函数磁压力的变 形计算[J]. 哈尔滨工业大学学报, 2010, 42(8): 1-2.
LIU Wen, LI Min, BAI Xiang-zhong, et al. Deformation calculation of electromagnetic Launcher’s rail subjected to exponential magnetic pressure[J]. Journal of Harbin Institute of Technology, 2010, 42(8): 1-2. (in Chinese)
[2] DANESHJOO K, RAHIMZADEH M, AHMADI R, et al. Dynamic response and armature critical velocity studies in an electromagnetic railgun [J]. IEEE Transactions on Magnetics, 2007, 43(1): 126-127.
[3] MANKOWSKI J,DICKENS J,GIESSELMANN M,et al.A bench top railgun with distributed energy sources [J]. IEEE Transactions on Magnetics,2007,43(1):167.
[4] ENGEL T, NERI J, NUNNALLY W, et al. Efficiency and scaling of constant inductance gradient DC electromagnetic launchers[J]. IEEE Transactions on Magnetics, 2006, 42(8): 2044-2047.
[5] DETHLFSEN R, MCNAB I. Pulse power applications of silicon diodes in EML capacitive pulsers [J]. IEEE Transactions on Magnetics, 1993, 29(1): 934-938.
[6] 王莹,肖峰.电炮原理[M].北京:国防工业出版社,1995:5-16.
WANG Ying,XIAO Feng.Electricity gun principle[M].Beijing:National Defense Industry Press,1995:5-16.(in Chinese)
[7] MCNAB I R. Early electric gun research [J]. IEEE Transactions on Magnetic, 1999, 35(1): 250-261.
[8] 姜仲秋, 汤承林. 电磁发射效率与激励电流关系的仿真[J]. 四川兵工学报, 2010, 31(3): 4-7.
JIANG Zhong-qiu, TANG Cheng-lin. Electromagnetic emission efficiency and incentive current relation simulation[J]. ACTA Armamentarii of Sichuan, 2010, 31(3): 4-7. (in Chinese)
[9] 龚兴根, 孙承纬, 周之奎, 等. 原理性电磁轨道炮的实验研究[J]. 爆炸与冲击, 1987, 7(2): 164-169.
GONG Xing-gen, SUN Cheng-wei, ZHOU Zhi-kui, et al. Experimental studies on the test electromagnetic railgun[J]. Explosion and Shock Waves, 1987, 7(2): 164-169. (in Chinese)
[10] 陈庆国, 王永红, 魏新劳, 等. 电容驱动型轨道电磁炮电磁过程的计算机仿真[J]. 电工技术学报, 2006, 21(4): 68-71.
CHEN Qing-guo, WANG Yong-hong,WEI Xin-lao,et al.Computer simulation of electromagnetic process in the capacitor drived rail gun[J]. Transactions of China Electrotechnical Society, 2006, 21(4): 68-71. (in Chinese)
[11] 郑庆生. 电磁学[M]. 上海: 华东师范大学出版社, 1999: 314-376.
ZHENG Qing-sheng.Electromagnetism[M].Shanghai:East China Normal University Press,1999:314-376.(in Chinese)

