非负矩阵谱半径的新界值
李 华
(河南城建学院数理系,河南 平顶山 467044)
非负矩阵谱半径的新界值
李 华
(河南城建学院数理系,河南 平顶山 467044)
非负矩阵谱半径的估计是非负矩阵理论中重要的课题。对Frobenius界值方法加以研究,给出了一种易于计算且能得到较紧的界的方法,并通过数值算例与以往的结果进行比较,有一定的精确性。
非负矩阵; 谱半径; 界值
非负矩阵在计算数学、图论等领域有着广泛的应用,对其谱半径的估计有着很重要的意义。非负矩阵谱半径的估计作为非负矩阵理论的核心问题之一,最著名且应用最多的估计由G.Frobenius[1]得到。
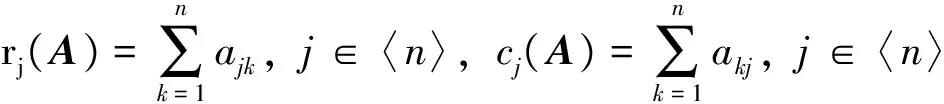
引理1[2]设A=(aij)为n阶非负矩阵,具有非零行和r1,r2,…,rn,则:
引理2[2]设α是矩阵A的特征值,X=(x1,x2,…,xn)T,Y=(y1,y2,…,yn)T分别是矩阵AT和A对应于α的特征向量,则:
引理3[2]若q1,q2,…,qn是正数,则对任意实数p1,p2,…,pn,有:
下面,笔者将在文献[3-5]的基础上对非负矩阵谱半径的估计作了进一步的研究。
1 主要结果
定理1设A=(aij)为n阶非负不可约矩阵,正对角矩阵X=diag(x1,x2,…,xn),记B=X-1AX,则有:

当X=diag(r1,r2,…,rn)时,即为引理1的结果。
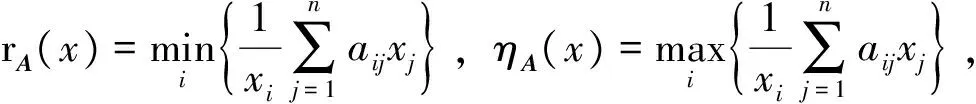
推论1设A=(aij)为n阶非负不可约矩阵,正对角矩阵X=diag(x1,x2,…,xn),记B=X-1AmX,Am=(aij)m,则有:
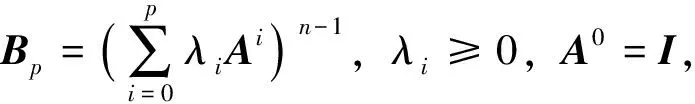
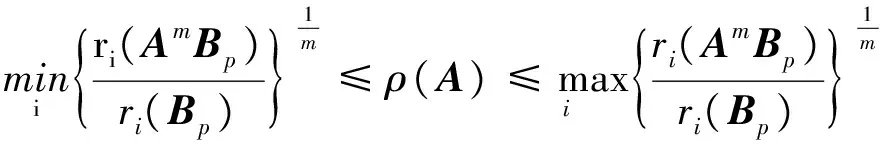

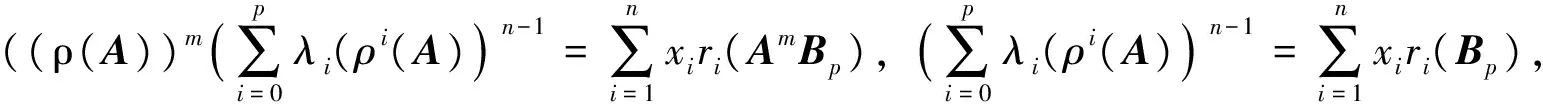
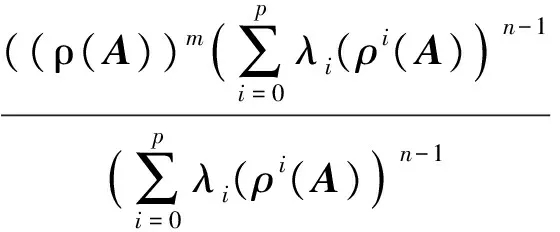
由引理3知:
注:对列和也有类似结论。
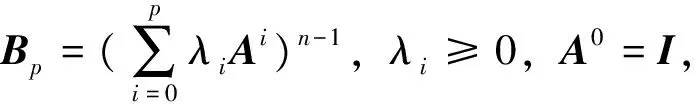
证明证明方法类似于文献[6]中定理4的证明,
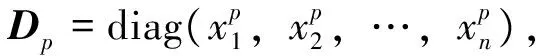

证明正对角矩阵D2可逆,对矩阵B2利用推论1可知:
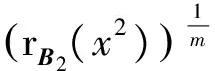
注: 对列和也有类似结论。
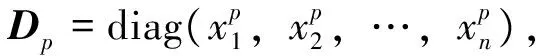
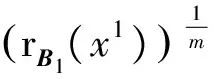
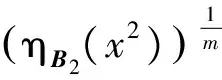
证明证明方法类似于文献[4]中定理4的证明。
2 数值例子

由文献[1]知,4≤ρ(A)≤8。由文献[2]知5≤ρ(A)≤6.25。在定理1中,m=1,p=2,λi=1,5.5995≤ρ(A)≤5.8257。m=1,p=3,5.68≤ρ(A)≤5.78。
实际上,ρ(A)=5.742,由此可知,定理1得到的结果在一定程度上要比以往的结果好。
[1]Frobenius.Uber matrizen aus nicht negativen elementen[M].Berlin: S B Press,1912:456-477.
[2]Minc H.Nonnegative Matrices[M].New York:Wiley,1988:11-19,24-36.
[3]殷剑宏.非负矩阵最大特征值的新界值[J].数值计算与计算机应用,2002,23(4):282-295.
[4]岳嵘.非负矩阵谱半径的新界值[J].数学的实践与认识,2009,39(17):206-209.
[5]孙文静,杨晋,刘彦芝,等.非负矩阵谱半径的新界[J].中北大学学报,2011,32(1):29-31.
[6]李丹青.非负矩阵谱半径的一个新界值[J].大学数学,2011,27(3):26-29.
[编辑] 洪云飞
10.3969/j.issn.1673-1409(N).2012.12.001
O151.21
A
1673-1409(2012)12-N001-03

