EPR堆芯严重事故下安全壳内的辐射屏蔽计算

曾 君，刘书焕，翟 良

（西安交通大学核科学与技术学院，陕西 西安710049）

核电作为一种清洁、高效的新能源，不能完全排除其发生事故的可能性，在能源日渐紧缺和环境问题日益严重的今天越来越受到各国关注。尽管核电厂有严密的预防措施，以保证核电厂的运行不会对广大公众以及核电厂工作人员造成放射性危害，但是当发生超设计基准的地震、海啸等极端自然灾害的情况时，包括初始事件叠加和失效叠加，还是会有可能发生堆芯熔化类的最严重事故。2011年3月，日本东部发生9.0级大地震并随之带来海啸，引发了福岛核电站的严重事故，大量放射性物质向环境不可控排放，对日本环境甚至对全球环境以及公众的心理都产生了不良影响。根据安全壳内辐射水平判断堆芯状况是国际上广泛采用的判断堆芯状况的方法，因此，在核电厂发生堆芯熔化等严重事故的情况下，根据核事故反应堆安全壳内的放射性核素浓度和辐射剂量的时空分布情况，推断堆芯熔化情况与压力容器、安全壳的可能损坏情况，是核电厂应急响应期间场外后果评价和确定应急防护行动的重要步骤。

在对堆芯的屏蔽因子计算中一般采用点核积分法和蒙特卡罗法。点核积分法[1]是一种格林函数积分方法，它用积累因子对γ光子的散射贡献进行了修正。而MCNP程序[2]是美国Los Alamos实验室应用理论物理部（X部）的Monte Carlo（X-6小组）研制的用于计算复杂三维几何结构中的粒子输运的大型多功能蒙特卡罗程序，它可以计算中子、光子、中子-光子耦合以及光子-电子耦合的输运问题，也可以计算临界系统（包括次临界和超临界）的本证值问题。

本文以台山核电站E P R堆芯为例，采用MCNP5程序及其核数据库CCC-710建立了精确的三维蒙特卡罗模型，在此基础上对EPR严重事故下安全壳内的辐射剂量率进行了计算与分析。

1 EPR堆芯的几何结构

根据美国USEPR中描述的EPR整定值构造了等效屏蔽系统，其MCNP几何模型如图1所示。

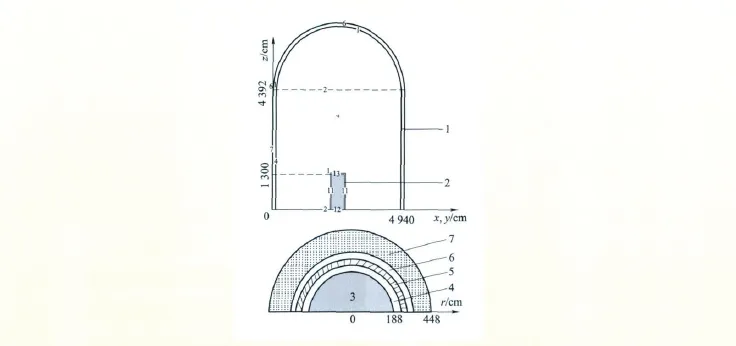
图1 EPR屏蔽计算模型示意图Fig.1 Shielding calculation model of EPR

2 问题的描述

2.1 对模型的假设

在模型的建立中主要有如下的假定：

1）堆芯活性区看作是一个均匀的铀水混合体，不同堆芯状况下的铀水比不同；

2）不考虑其他设备放射源的贡献；

3）放射性物质在安全壳内均匀混合；

4）堆芯熔化事故处于事故初期阶段，此时屏蔽系统完好无损；

5）为了减少运算的工作量并降低方差，针对各类屏蔽材料，构造了一个虚拟球把整个屏蔽系统包裹起来；粒子打在球以内则对该粒子继续进行跟踪，否则重新抽样。

2.2 对源的描述

在计算台山核电站EPR堆芯在严重事故工况下的光子注量率分布时，核素的选取应依据它们在堆芯的总存量，是否容易从堆芯释放以及释放入安全壳内对辐射监测仪表读数的贡献等因素考虑。此外，在反应堆内各材料位置γ光子剂量当量率的计算中，计数器的位置与注量率的计算位置相同，通过乘子卡实现注量率到γ剂量率的转换。

在源描述中，采用通用源卡SDEF只对光子进行抽样。按照EPR的堆芯功率1750 MW，设计时采用大容积双层安全壳（8万m3），将EPR在堆芯熔化事故状况下作为研究其辐射特性的基础，将EPR以额定功率正常运行工况下的辐射水平作为对比；通过归一化计算得到源强常数4.1×1019s-1，并设为各向同性；而计算的对源粒子抽样使用的光子能谱列于表1。计算时选择的各项参数如下：

1）核素在堆芯和一回路的总存量取自核电厂运营商；

2）堆芯熔化时核素从堆芯的释放份额取自文献[3]；

3）核素的光子能量与产额数据取自文献[4]。

2.3 对屏蔽材料的描述

屏蔽计算系统划分为12个区域，包括堆芯、围板、反射层、吊篮、热屏蔽、压力容器和混凝土屏蔽层等（见图1）。组件中心距为21.5 cm。计算中假设堆芯是一个由多种材料组成的均匀混合体，高度为420 cm，等效当量直径为376.7 cm。堆芯外面依次被围板、反射层、吊篮、混凝土等屏蔽材料包围。围板、吊篮、热屏蔽均采用不锈钢材料（M3310），密度为7.9 g·cm－3。压力容器材料为法国A508-III钢（16MND5）[5]，密度为7.85 g·cm-3。压力容器周围由8.5 cm厚的不锈钢保温层包围。反应堆中各区域的核密度及材料的描述列于表2。

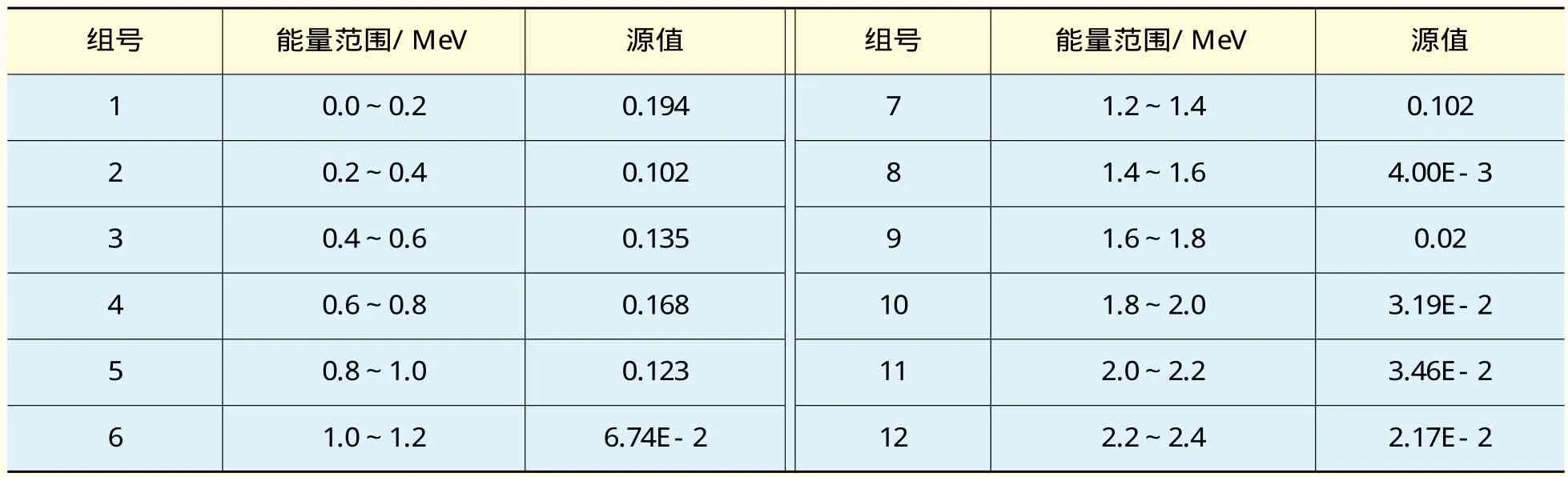
表1 光子能谱Table1 Energy spectrum of photons

表2 堆芯各区域密度Table2 Nucleus density of various core regions

3 计算结果和分析

3.1 计算条件

在对γ射线的屏蔽计算研究中，屏蔽材料性能的数据的准确性非常重要。然而，即使MCNP的统计误差再小，模拟条件与实际条件再接近，模拟的计算结果与理论值计算的结果一般不能完全符合。但是MCNP程序以它跟踪粒子逼真，不受求解问题边界条件、维数的限制等特点[6]，在粒子输运领域的应用日益广泛，其结论还是非常具有参考价值的。

本文γ剂量率的计算采用MCNP跟踪模拟2000万个光子的运动，衰变光子输运的计算结果EPR压力容器外壁注量率误差在5%以内，而混凝土屏蔽层外壁注量率的统计误差控制在10%以内；从注量率到剂量率的转换使用了DEn及DFn剂量转换卡，所使用的光子注量率-剂量率转化因子取自手册“MCNP-A General Monte Carlo N-Particle Transport Code, Version5”，列于表3。

3.2 γ剂量率结果及分析

根据核素从堆芯的释放份额、材料均匀化的核密度及相关的EPR堆芯本体结构参数，计算了正常运行和堆芯熔化下安全壳内的γ剂量率。图2给出了EPR在正常运行和堆芯熔化状况下混凝土屏蔽层以内γ剂量率沿径向的分布情况。可以看出，两种工况下混凝土屏蔽层以内γ剂量率沿径向分布的规律相似：在堆芯活性区内，剂量率下降的很少；而随着在混凝土屏蔽层中径向距离的增大，剂量率下降的趋势明显。在正常运行工况下，混凝土屏蔽层外壁剂量当量率为4.89×10-2m S v·h－1，已满足正常运行工况下主屏蔽混凝土外表面设计剂量限值≤1.5×10-1mSv·h-1的要求；在堆芯熔化状况下，混凝土屏蔽层外壁剂量当量率为1.02×101mSv·h－1。

辐射剂量水平是判断堆芯是否熔化，压力容器、安全壳是否损坏的主要参考因素，是核电厂应急响应期间场外后果评价和确定应急防护行动的重要步骤。在不考虑混凝土生物屏蔽层的情况下，堆芯装水量与安全壳内辐射剂量率的关系如图3所示。从堆芯完全裸露到水完全覆盖堆芯，安全壳内的辐射水平随着堆芯水量的上升呈直线下降的趋势，且装水量每增加25%的体积比例，γ剂量率就下降了6个数量级左右；当屏蔽层换成35 cm厚的压力容器时，安全壳内壁剂量率比25 cm时的大约低20～30倍。在假设堆芯完全裸露、屏蔽系统遭到破坏且全部核素瞬间释放到安全壳内的情况下，安全壳内封头处的γ剂量率为5.02×106mSv·h－1；而当水完全覆盖住堆芯时，此时安全壳内的γ剂量率可以视作忽略不计。

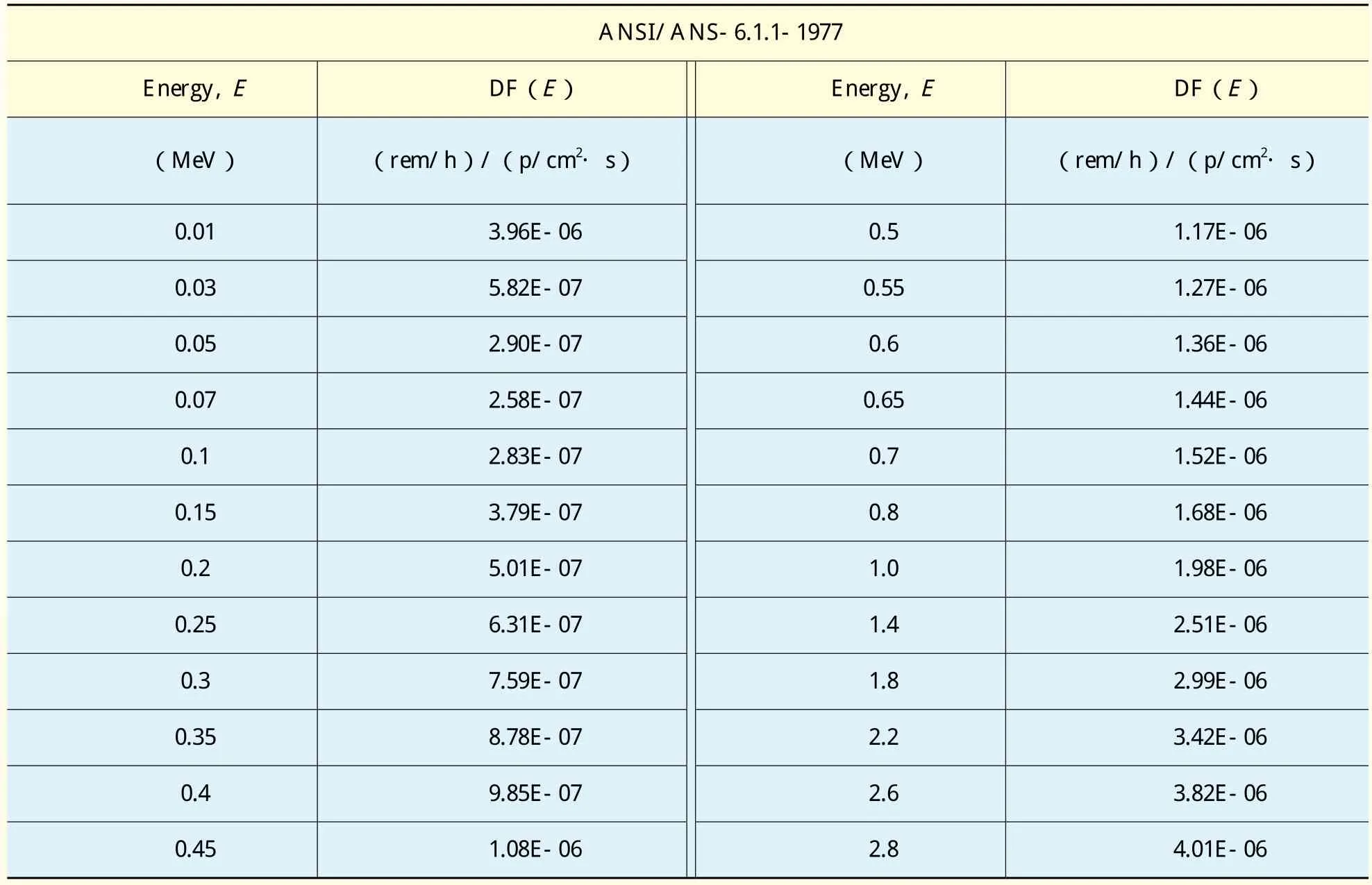
表3 光子注量率-剂量率转化因子Table3 Photon flux-to-dose rate conversion factors

图4给出了EPR正常运行工况下压力容器和混凝土生物屏蔽层外壁剂量率周向和轴向的分布情况。可以看出对于整个屏蔽系统来说，沿周向和轴向的分布规律大体相似。由于热屏蔽被吊篮、围板等在此模型中一起视作等效屏蔽体，所以周向上剂量率并未出现20°以内有明显低于其他周向的趋势，而是在一定范围内随着周向的增大而增大。压力容器与混凝土屏蔽层外壁剂量率轴向分布大致沿着中平面对称，且最高值基本上都出现在中平面附近。压力容器外壁剂量率最高值为5.68×104mSv·h－1，在周向40°轴向0 cm处；最小值为1.47×104mSv·h－1，在周向0°轴向-40 cm处。混凝土屏蔽层外壁剂量率最高值为4.89×10-2mSv·h－1，在周向35°轴向0 cm处；最小值为1.06×10-2mSv·h－1，在周向5°轴向40 cm处。剂量率从压力容器外壁到生物屏蔽层外壁大约下降了6个数量级。

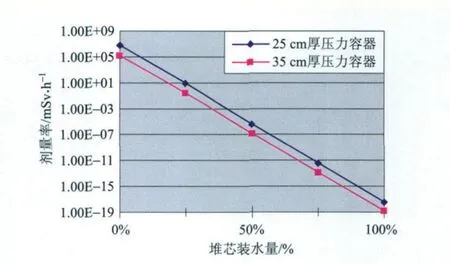
图2 屏蔽系统内γ射线剂量率径向分布图Fig.2 Radial distribution of γ-ray dose rate within shielding system

图3 堆芯不同裸露状况下安全壳内的剂量率Fig.3 Dose rate in containment under different core damages

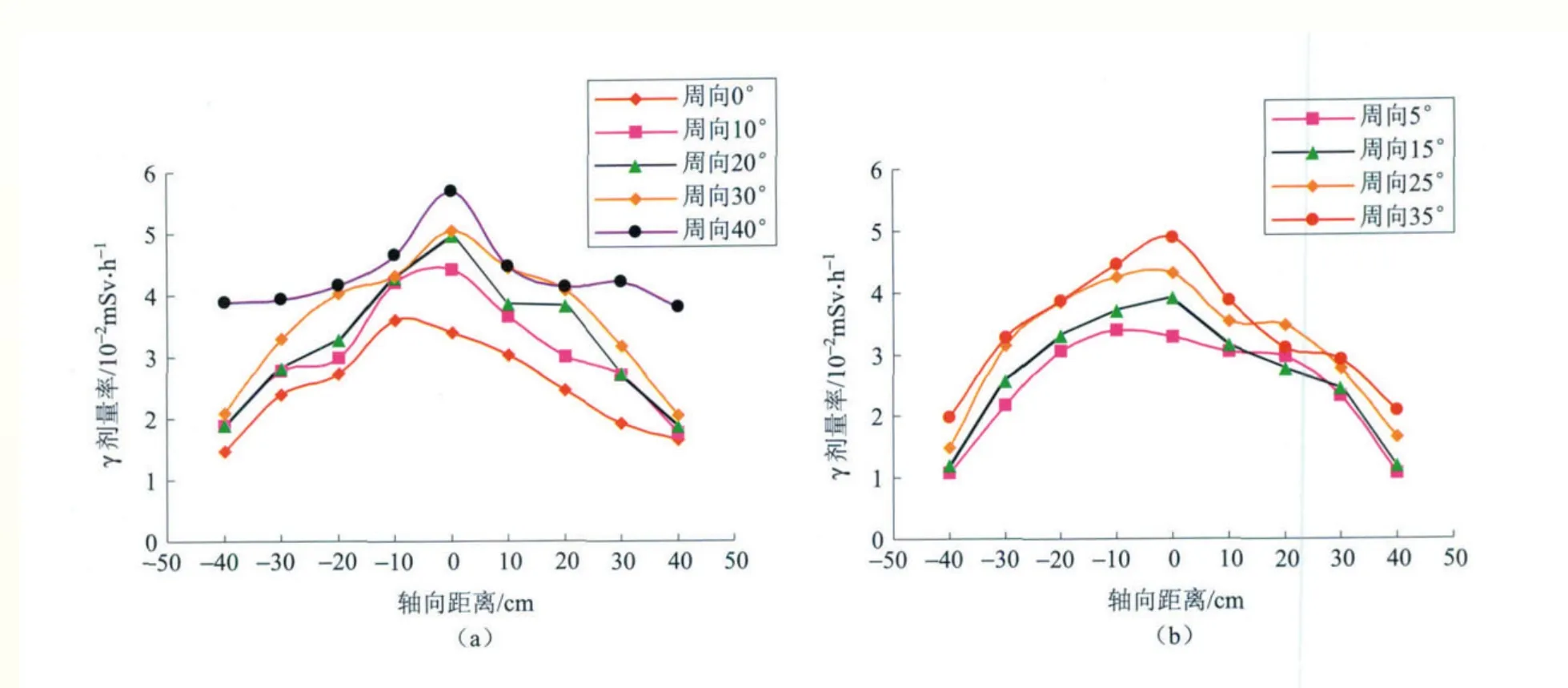
图4 正常运行工况下压力容器（a）和混凝土屏蔽层(b)外壁剂量率分布Fig.4 Dose rate distribution in outer RPV (a) and primary concrete (b)under normal operation condition

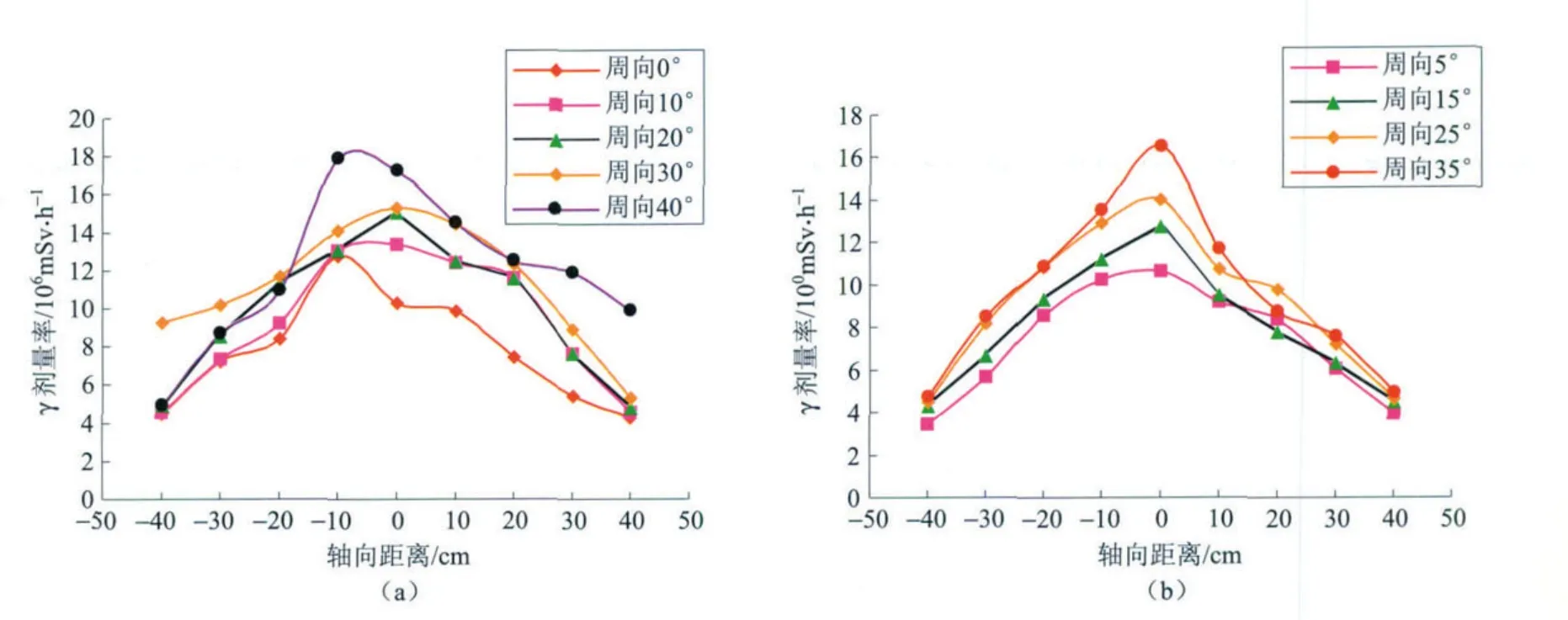
图5 堆芯熔化工况下压力容器（a）和混凝土屏蔽层（b）外壁剂量率分布Fig.5 Dose rate distribution in outer RPV (a) and primary concrete (b)under core melt condition

图5给出了E P R堆芯熔化工况下压力容器和混凝土生物屏蔽层外壁剂量率周向和轴向的分布情况。可以看出，两者外壁剂量率沿0°到40°的周向分布规律相似且逐渐升高。外壁剂量率轴向分布基本沿中平面对称，个别最高值出现在轴向-10 c m处，最小值都位于轴向两端。其中，压力容器外壁剂量率最高值为17.90×106mSv·h－1，在周向40°轴向-10 cm处；最小值为4.3×106mSv·h－1，在周向0°轴向40 cm处。混凝土屏蔽层外壁剂量率最高值为1.65×101mSv·h－1，在周向35°轴向0 cm处；最小值为3.49 mSv·h－1，在周向5°轴向-40 cm处。从整体上来说，假设屏蔽层都存在的话，EPR堆芯在熔化工况下比正常运行时安全壳内的γ剂量率要高了2个数量级左右。

3.3 对计算结果的影响因素

在运用蒙特卡罗程序MCNP5计算EPR不同堆芯状况时的辐射剂量水平时，还采用了多种有效的方法来降低计算的方差，如使用虚拟球，调整粒子的权重，使用纠偏因子等。在计算2000万个光子的条件下，使蒙特卡罗的统计误差在可接受的范围之内。对于MCNP5程序来说，影响计算结果的因素除了参数的不确定性外，蒙特卡罗方法本身固有的统计误差最大也达到了10%左右，特别是某些栅元之间的边界点；堆芯的结构、布置，压力容器、屏蔽层的材料、密度也是引起计算时另一个不确定性的因素；对源强估算的不确定性同样也是不可忽视的。

4 结论

运用MCNP的方法计算EPR堆芯严重事故下安全壳内辐射剂量水平是一种可行的方法，程序本身的统计误差和方差对计算结果准确性的影响不容忽视。当混凝土厚度为220 cm时，正常运行工况下生物屏蔽层外最大剂量当量率为4.89×10-2mSv·h－1，小于设计限值；但是在堆芯熔化初期、屏蔽系统完好无损的情况下，生物屏蔽层外最大剂量当量率为1.65×101mSv·h－1，远大于这一限值。此时，应急响应部门应做好事故核电厂释放或潜在释放的放射性物质随时可能威胁到场内员工和场外公众、采取应急防护行动、保护场内外人员的安全和健康的准备。MCNP方法虽然不一定很精确，但对于核事故应急有一定的指导意义，值得进一步深入探索。

[1]Graf O. Inter comparison of Three Shielding Codes for External Radiation from Deposition Material, Proceedings “Workshop on Methods for Assessing the off-site Radiological Consequences of Nuclear Accidents”.Luxembourg,15～19 April1985.439－450.

[2]Briesmeister J F. MCNP: A General Monte Carlo N-particle Transport Code, Version4C [R].LA-13709-MUSA:LANL,2000.

[3]U.S NRC. Accident Source Terms For Light－Water Nuclear Power Plant[R]. NUREG-1465，1995.

[4]NRC U.S. The Mesorad Dose Assessment Mode[R]. NUREG/CR-4000 Vol.1. Washington:USNRC,1986.

[5]李承亮，张明乾. 压水堆核电站反应堆压力容器材料概述[J]. 材料导报，2008，22（9）:66.（L I N Cheng-liang, ZHANG Ming-qian. Overview of RPV materials of PWR NPP [J]. Materials Review,2008,22(9)：66.）

[6]胡二邦，高占荣. 大亚湾地区建筑物辐射屏蔽因子的计算[R]. CNIC-01429，CIRP-0029.（HU Erbang, GAO Zhan-rong. Radiation shielding factor calculation for buildings near Daya Bay NPP [R]. CNIC-01429, CIRP-0029.）